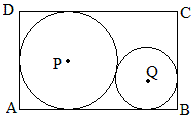等边三角形具有轴对称性和旋转对称性，四平八稳的图形却可以构造出千姿百态的图形，是三角形中最具魅力的图形。因为正三角形的一半是特殊的直角三角形，所以正三角形的问题又常常转化为直角三角形来解决。今撰斯文，欲展示正三角形的众多性质，你读罢定会感慨频频。
几何作图题的征解结果
没想到才过4天，一道几何作图题征集到多人的解答，并在QQ群（出众树雪88730268）上引起大讨论，看来数学研究就得这样，有问题大家研究，有结果大家分享。
一、问题提出
问题1
一位老师问我：在一个长8厘米、宽6厘米的长方形内画两个圆，这两个圆的面积之和最大是多少？
因为百思不得其解，于是想用几何画板绘制图形，以探索最大值的位置。但作图遇到了困难，也就是
征求解答：一道几何作图题
在几何画板中想作如下的图形，结果发生了困难，请教高手解答。
给定矩形ABCD，先作一个最大的圆P，要在余下的矩形区域内再作一个最大的圆Q。
可是圆Q的圆心如何确定呢？我百思不得其解。也就是在已经画出矩形ABCD和圆P后怎样用尺规作出圆Q，请大家支招！
我分析来分析去，最终将问题转化为如下的作图题。
已知∠ABC=45°，定点P在角内部，请在射线BC上找一点Q，使得Q到AB的距离等于PQ。
以上问题等待你的解答，求助了。
教育界的怪现象
虽说“臭老九”变成了“香馍馍”，想当教师的人越来越多，但教育界的怪现象也越来越多。以前不是这样的，从教30多年的我越来越看不懂。众人前不敢讲的话、许多人满肚的牢骚，我都憋着憋着……。有些话题实在很敏感，但在这儿发泄一下也无妨。
一、没有教不会的学生，只有不会教的老师
不知是哪位专家的语录，我对第一句话特反感。我找几个学生让这位专家来教教，看看有没有教不会的学生。我们撇开智障、智残的学生不说，到了初中乃至高中，那些丢失基础，连家长都彻底失望的学生比比皆是。你一个专家竟然能说“没有教不会的学生”？你教了几年书？遇到过多少类型的人？
对反比例函数图象的新认识
反比例函数有许多性质，经过同行们的不断探索，又发现了新的性质，今列举如下，供大家研究。
计算器的使用与初中数学双基教学
一、前言
我国2001年颁发的《数学课程标准》指出：“能借助计算器进行复杂计算和探索数学规律……。在课堂教学、课外作业、实践活动以及考试中，应当允许学生使用计算器。”
由此可见，计算器进入初中数学课堂势在必行。以前，由于禁止学生使用计算器，结果加重了双基教学的任务，为了应付复杂的计算，学生从小学到初中都要进行大题量的操练。现在，计算器成了初中学生必不可少的学习工具，学生不仅仅摆脱了复杂的计算，而且改变了学习方式、思维方式，学习效益大为提高。
本文谈谈怎样正确引导学生合理使用计算器，使计算器成为促进双基教学的工具。
享受生活源于汉兰达
每篇文章都是关于数学的，学术气太重，太严肃了。今儿想换个口味，写一点生活。
我的爱车“汉兰达”（以下简称大汉）上路已有3月余，每当有人问及：“这车咋样？”时，我都不加思索答道：“现在才知什么叫好车”。其实我也是井底之蛙，真正的好车连坐都没坐过呢。
有一种理想叫梦想，我从小做梦开着车到处跑。有一种盼望叫等待，我知道换一辆新车只是时间问题。有一种享受叫尝新，卖这买那地折腾、体验各种人性化的功能都是其乐无穷的。有一种发泄叫倾诉，我想把选车的经历、开车的体会和对大汉的测评书于博客。一来满足自己，二来供购车族参考。
学生妙解数学题3
前面已经有很多学生妙解的例子了（共18题），具体的见：
自从我留心学生巧妙的解法，真的对学生有了新的认识：人的能力不可小视，一切皆有可能！有兴趣的你点进去看看，保证你拍案叫好。
今另起一文，再陆续摘录我学生的妙解。
关于sinα+cosα最大值的解答征集
为了提高本博客的互动性，我在上篇文章《征求解答》中提出了一个初中数学问题：
如果\alpha为锐角，那么sin{\alpha}+cos{\alpha}的最大值为\sqrt{2}。
请你将证明过程在下面评论里给出，证明的依据不能超过初中知识。
本问题的结论是我很早时候自己发现的，我想一定会引起更多老师的兴趣。结果征集到五位老师的四种解答（有些解答在QQ中交流），公布如下。
征求解答
命题：如果\alpha为锐角，那么sin{\alpha}+cos{\alpha}的最大值为\sqrt{2}。
请你将证明过程在下面评论里给出，证明的依据不能超过初中知识，证明正确者，将获得2010年中考数学分类试卷一套的奖励。你也可以在其它网页里发表解答过程，将地址列出。请注明接收奖励文件的地址。