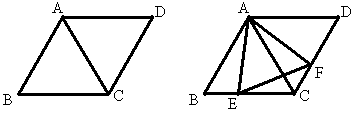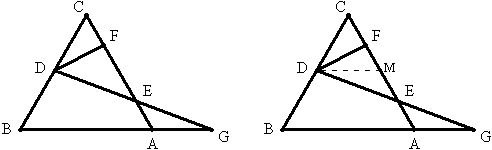等边三角形具有轴对称性和旋转对称性,四平八稳的图形却可以构造出千姿百态的图形,是三角形中最具魅力的图形。因为正三角形的一半是特殊的直角三角形,所以正三角形的问题又常常转化为直角三角形来解决。今撰斯文,欲展示正三角形的众多性质,你读罢定会感慨频频。
一、三垂线
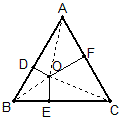
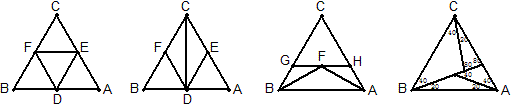
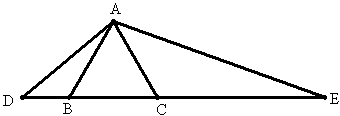
例1 如图O是正三角形ABC内任意一点,过O点作三边的垂线,垂足分别为D、E、F,求证:OD+OE+OF等于正三角形的高。
证明:连结OA,OB,OC,设正三角形高为h,因为S_{\triangle{AOB}}+S_{\triangle{BOC}}+S_{\triangle{AOC}}=S_{\triangle{ABC}}
所以,\frac{1}{2}\times{AB}\times{OD}+\frac{1}{2}\times{BC}\times{OE}+\frac{1}{2}\times{AC}\times{OF}=\frac{1}{2}\times{AB}\times{h}
因为AB=BC=CA,
所以OD+OE+OF=h.
例2 如图O是正三角形ABC内任意一点,过O点作三边的垂线,垂足分别为D、E、F,求证:AD+BE+CF=BD+CE+AF.
解法一
利用勾股定理,有AD^2+OD^2=AF^2+OF^2,类似地还有其他2个等式,三个式子相加,化简得到:
AD^2+BE^2+CF^2=BD^2+CE^2+AF^2,
即AD^2+BE^2+CF^2=(a-AD)^2+(a-BE)^2+(a-CF)^2
化简:AD+BE+CF=\frac{3a}{2},a是正三角形的边长。
解法二
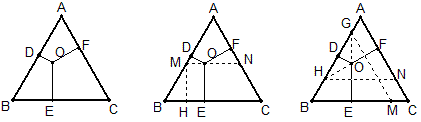
如图,过O作MN∥BC,交AB、AC于点M、N,过M作MH⊥BC交BC于点H,
则AD+BE+CF=AD+2MD+\frac{1}{2}BM+BM+\frac{1}{2}(AM-2MD)=AD+MD+BM+\frac{1}{2}(BM+AM)=\frac{3}{2}AB,
同理BD+CE+AF=\frac{3}{2}AC,
∴AD+BE+CF=BD+CE+AF.
又:
在这种辅助线下,还可以设DO=x,OE=y,OF=z,
于是正三角形的高是x+y+z,从而边长可以被表示,MD,MH,BM可以表示。
进而AD可以表示,这样表示BE,CF也不难了,AD+BE+CF就可以被x,y,z来表示。
可以肯定AD+BE+CF表示后的结果一定是周长的一半。
解法三
如图,延长EO、FO交边于G,H,过G,H作边的平行线GM,HN,
则AD+BE+CF=(DH+MC)+EM+(BH+AF)=BD+CE+AF.
例3 如图O是正三角形ABC内任意一点,过O点作三边的垂线,垂足分别为D、E、F,求证:S_{\triangle{AOD}}+S_{\triangle{BOE}}+S_{\triangle{COF}}=\frac{1}{2}S_{\triangle{ABC}}。
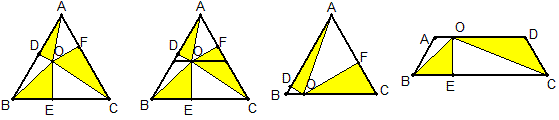
解:过O作BC的平行线,将三角形分成上下两部分,如图,上部分相当于证明O在BC上时,黄色部分面积为正三角形面积的一半。证明如下:
设AB=2a,∴OD+OF=\sqrt{3}a,设OF=x,则AD=2a-\frac{\sqrt{3}a-x}{\sqrt{3}}=a+\frac{x}{\sqrt{3}},
则黄色面积=\frac{1}{2}(\sqrt{3}a-x)(a+\frac{x}{\sqrt{3}})+\frac{1}{2}\frac{x}{\sqrt{3}}x
=\frac{\sqrt{3}}{2}a^2=\frac{1}{2}S_{\triangle{ABC}}.
如图,对于下半部分的证明类似。故结论得证。
二、三交线
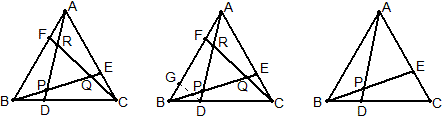
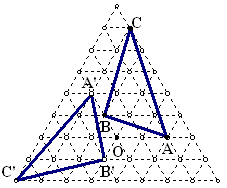
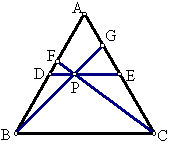
如图,在正三角形ABC的三边上依次取BD=CE=AF,连AD、BE、CF,交点是P、Q、R,这个图的内部有三条交线,里面形成一个正三角形,两个正三角形的面积之比取决于BD和DC之比。如果去掉一条交线,又会得到一个熟知的图形。
例4 如上图及已知,当BD:DC=1:n时,求小正三角形与大正三角形面积的比。(自编题)
解:过D作DG∥CF,则可证BG:GF:FA=1:n:\frac{n+1}{n},
进而AR:AD=FR:GD=\frac{n+1}{n}:(\frac{n+1}{n}+n)=\frac{n+1}{n^2+n+1},
又DG:FC=1:(n+1),∴FR:FC=\frac{n+1}{n^2+n+1}\times\frac{1}{n+1}=\frac{1}{n^2+n+1},
所以RQ:FC=1-\frac{1}{n^2+n+1}-\frac{n+1}{n^2+n+1}=\frac{n^2-1}{n^2+n+1},
在△ABD中设BD=1,AB=n+1,
∵∠ABD=60°,∴AD=\sqrt{n^2+n+1},
∴AD:AB=\sqrt{n^2+n+1}:(n+1),
∴RQ:AB=\frac{\sqrt{n^2+n+1}}{n+1}\times\frac{n^2-1}{n^2+n+1}=\frac{n-1}{\sqrt{n^2+n+1}},
由两个正三角形相似得,小与大的面积之比是RQ^2:AB^2=\frac{(n-1)^2}{\sqrt{n^2+n+1}}。
例5 如上图,正三角形ABC中,BD=CE,BE、AD交于P写出这个图形尽量多的性质。(自编题)
解:①有2对全等三角形;②有6对相似三角形;③∠APE=60°;④BD^2=DP\times{DA}、AE^2=EP\times{EB}。
三、到三顶点的距离
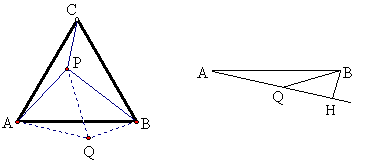
例6 如图,P在正三角形ABC内,P到三个顶点的距离分别是3、4、5,求△ABC的面积(精确到0.01)。
解:如图,将△APC绕A点顺时针旋转60°至△AQB,设QB=PC=3,QP=AP=4,PB=5,易证∠APC=∠AQB=150°,如左图,作BH⊥AQ,因∠BQH=30°,故BH=1.5,AH=4+\frac{\sqrt{3}}{2},由勾股定理可以求出AB,进而求出面积的近似值。
四、正三角形拼图
1、三角板拼图
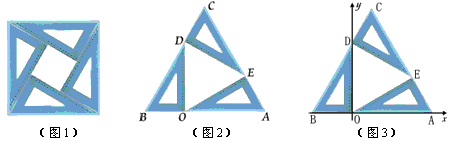
例7 如图1是由四块全等的含有30°角的直角三角板拼成的正方形,已知里面小正方形的边长为\sqrt{3}-1.如图2,取其中的三块直角三角板拼成等边三角形ABC,再以O为原点,AB所在直线为x轴建立平面直角坐标系.(自编题)
(1)求等边△ABC的面积;
(2)求BC边所在直线的解析式;
(3)将第四块直角三角板与△CDE重合,然后绕点E按逆时针方向旋转60°后得△EC’D’ ,问点C’是否落在直线BC上?请你作出判断,并说明理由.
解略。
2、两个正三角形拼菱形
例8 两个正三角形拼成一个菱形ABCD,(1)此菱形有哪些性质?(2)在BC、CD上各取一点E、F,使BE=CF,求证:△AEF是正三角形。
解:(1)较长对角线是较短对角线的\sqrt{3}倍;过A点的高平分BC;有120°的内角。在菱形中只要满足这三条之一的,必满足其余。(2)略
3、三个正三角形拼梯形
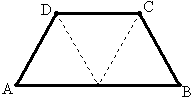
例9 如图,三个正三角形拼成等腰梯形,此梯形有哪些性质?(自编题)
解:①有60°的底角;②下底是腰的一半;③周长是腰的5倍;④对角线AC垂直腰BC;⑤对角线平分60°的底角;⑥上底等于腰。一个等腰梯形具有这6个结论中的任意2个,必同时满足其余的结论。
五、正三角形内的正方形
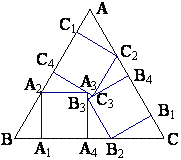
例10 如图,正△ABC中,BC=2\sqrt{3}+3,在BC上取一点A1,作A1A2⊥BC交BC于A2,在△ABC内部作正方形A1A2 A3A4。过A3点作AB的垂线交AB于C4,在△ABC内部作正方形C1C2 C3C4,其中C1在AB上,C2在AC上,并且所作的两个正方形边长相等。又过C3点作AC的垂线交AC于B4,交A3A4于B3,在△ABC内部作正方形B1B2 B3B4,其中B1在AC上。(自编题)
(1)求A1A2的长;
(2)求证:正方形B1B2 B3B4的边长与正方形A1A2 A3A4的边长相等;
(3)求证:B2在BC上。
解:(1)设正方形的边长为x,则A_2B=\frac{2}{3}\sqrt{3}x,A_2C_4=\frac{1}{2}x,C_1A=\frac{1}{3}\sqrt{3}x
所以\frac{2}{3}\sqrt{3}x+x+\frac{1}{2}x+\frac{1}{3}\sqrt{3}x=2\sqrt{3}+3,解之x=2。
(2)易证\triangle{A_3B_3C_3}是正三角形,\triangle{A_3A_2C_4}\cong\triangle{C_3C_2B_4},
所以A_3C_3=B_3C_3,A_3C_4=C_3B_4,即C_3C_4=B_3B_4,
故正方形B_1B_2B_3B_4的边长与正方形A_1A_2A_3A_4的边长相等。
(3)B_1C=AC-AC_2-C_2B_4-B_4B_1=2\sqrt{3}+3-\frac{4}{3}\sqrt{3}-1-2=\frac{2}{3}\sqrt{3},
又因为B_1B_2=2,由勾股定理得B_2C=\frac{4}{3}\sqrt{3},故\angle{B_1CB_2=60^\circ},
即B2在BC上。
六、两个正三角形组合
两个正三角形可以组成许多有趣的图形,有些图形的结论还鲜为人知呢。
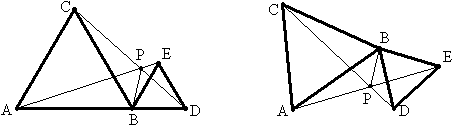
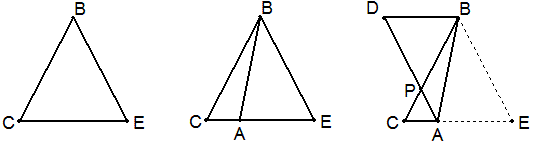
例11 如图△ABC和△BDE均为正三角形,AE和CD交于P。(1)当A、B、D共线时,求证:∠APB=∠DPB=60°;(2)当A、B、D不共线时,∠CPB=∠EPB=60°吗?为什么?
解:两个问题的证明完全一样。
作△ABE和△CBD的高BG、BH,有这两个三角形全等可知,BG=BH,所以BP平分∠APD(或∠CPE),因△ABE和△CBD可以看作绕B点旋转90°重合的,所以对应边AE和CD所成的角为60°,即∠APC=60°,故结论成立。
思考:如果将△EBD沿BD反射,结果又会怎样呢?
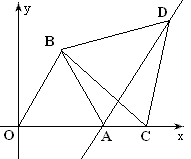
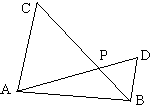
例12 如图,△AOB和△BCD均是正三角形,点O是坐标原点,A(2,0),C是x轴上一点,D、O在BC异侧,问:当C点运动时,D点运动的轨迹是什么?(也可以问:当C点运动时,直线AD是否固定?为什么)
解:可以证明△OBC≌△ABD,所以∠BAD=60°,所以D点运动的轨迹是直线y=\sqrt{3}x-2\sqrt{3}。
思考:
(1)将条件“D、O在BC异侧”改为“D、O在BC同侧”,结论又如何呢?
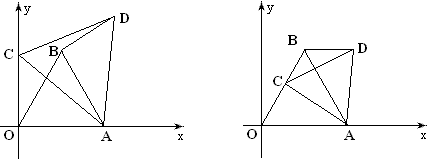
(2)如下图,如果将条件“C是x轴上一点”改为“C是y轴上一点”,“正三角形△BCD”改为“正三角形△CAD”,BD和AB的关系如何呢?
(3)如下图,如果将条件“C是x轴上一点”改为“C是OB上一点”,“正三角形△BCD”改为“正三角形△CAD”,DB和OA的关系如何呢?
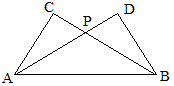
例13 判断命题“△ABC和△ABD有公共边AB,且C、D在AB同侧,如果AD和BC相交且相等,那么△ABC≌△ABD”是否成立?
解:如果我们画出如下的图形,可能很难判断命题的真假。
注意,并不能因为是“边边角”就判断是假命题,关于“边边角”的更多内容,请参见“引人入胜的SSA”。
本命题确为假命题。以前,我举的反例是:
在正三角形BCE中,A是CE上的点(非中点),将△ABE绕AB的中点旋转180°得到△ABD,这就是反例。
后来找到了用两个正三角形来组成反例的图形:
如图,△APC和△BPD均为正三角形,A、P、D共线,这个图形就是反例。
思考:用两个等腰三角形来代替△APC和△BPD可以吗?
七、正三角形分割
例14 用多种方法将正三角形分割成4个等腰三角形。
解:至少有以上4种分割方法。值得惊奇的是居然有一种不对称的分割。
思考:还有其它方法吗?
例14-2 以下两个图形是一个等腰Rt△ABC和一个等边△DEF,要求把它们分别分割成3个三角形,使得△ABC分出的3个三角形与△DEF分出的3个三角形分别相似。
解:我想到以下几种方法,一定还有其它方法哦,想到了再补充。
追加:
2011年4月28日江东区的数学教研活动中,专题研究了本题,同行们又得出了以下4种不同的分割方法:
八、找等腰点
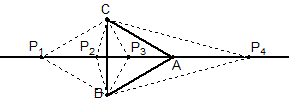
例15 已知正三角形ABC,在平面上找一点P,使△ABP、△BCP、△CAP均为等腰三角形,这样的P点有 种不同的位置。
解:如图,在BC的中垂线上符合条件的点有4个,而边的中垂线有3条,故共有10个不同的位置(其中形内只有一点)。
九、正三角形网格
正三角形网格能发挥正方形网格力不能及的作用,在正三角形网格图中,能呈现五彩缤纷的数额学问题。
例16 如图,在正三角形网格中有个格点△ABC及格点O,请画出△ABC以点O为旋转中心逆时针旋转120°的像。
解:△A’B’C’就是所求的像。
我们常常在正方形网格里将一个图形旋转90°,为什么不可以在正三角形网格里将一个图形旋转60°或120°呢?
例17 如图把边长为4的正三角形各边四等分,连结各分点得到16个小正三角形.
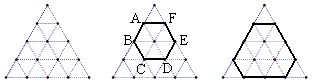
(1)在图1中,画出以小正三角形的顶点为顶点的一个正六边形ABCDEF,并求这个正六边的周长.
(2)请你判断:命题“六个内角相等的六边形是正六边形”是真命题还是假命题?如果是真命题,请你把它改写成“如果……,那么……”的形式;如果是假命题,请你在图2中画图说明.
解:略。
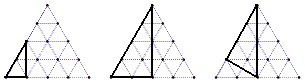
例18 在如图的正三角形网格中,画出格点三角形,使三边之比为1:\sqrt{3}:2,这样的三角形面积是值有 种。
我的答案只有如图3种,不知是否还有?
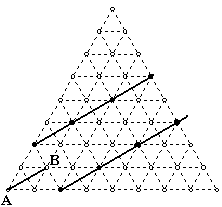
例19 如图,在正三角形网格中,一个小正三角形的面积为1,给定2个格点A、B,请你再找一个格点C ,使得△ABC的面积为2,这样的C点共有 种不同的位置。
解:利用平行线面积不变的原理,如图共可以找到8个不同的位置.
例20 如图是一个由基本图形经过若干次平移后得到的图形,这个基本图形可以是( )
解:答案是C,只要将6个C的图形组合在一起即可。
十、杂题
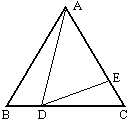
例21 如图正三角形ABC中,D是边BC上一点,E是AC上一点,∠ADE=60°,(1)若BD=3,CE=2, 求AE;(2)当AB=8时,求CE的最大值。
解:(1)设AB=x,由△ABD∽△DEC得,x:(x-3)=3:2,x=9,所以AE=9-2=7.
(2)设BD=x,EC=y,由△ABD∽△DEC得,x:y=8:(8-x),则y=-\frac{1}{8}(x-4)^2+2,所以y的最大值是2.
例22 如图,正三角形ABC的边长为a,P是中位线DE上一点,直线BP、CP交边于G、F,则\frac{1}{BF}+\frac{1}{CG}= 。
方法一:用特殊位置法解
当P与D重合时,BF=\frac{a}{2},CG=a,\frac{1}{BF}+\frac{1}{CG}=\frac{2}{a}+\frac{1}{a}=\frac{3}{a}.
方法二:
设GE=m,DF=n,PE=x,则PD=\frac{a}{2}-x.
由△GPE∽△GBC得,\frac{m}{m+\frac{a}{2}}=\frac{x}{a},
由△FPD∽△FCB得,\frac{n}{n+\frac{a}{2}}=\frac{\frac{a}{2}-x}{a},
分别解得m=\frac{ax}{2(a-x)},n=\frac{a^2-2ax}{2(a+2x)},
故CG=\frac{ax}{2(a-x)}+\frac{a}{2}=\frac{a^2}{2(a-x)},
BF=\frac{a^2-2ax}{2(a+2x)}+\frac{a}{2}=\frac{a^2}{a+2x},
所以,\frac{1}{BF}+\frac{1}{CG}=\frac{2(a-x)}{a^2}+\frac{a+2x}{a^2}=\frac{3}{a}.
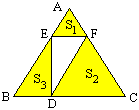
例23 如图,△AEF和△CDF是正三角形ABC内的两个正三角形,已知S_1=a,S_2=b,求S_3的值。
自己编的,解答留给读者吧。
例24 如图△ABC是边长为6的正三角形,直线BC上取两点D、E,使∠DAE=120°,(1)试写出3个比例中项的式子;(2)已知BD=4,求AE的长。
解:(1)BC^2=BD\times{CE},AD^2=BD\times{DE},AE^2=EC\times{ED};
(2)由BC^2=BD\times{CE},得CE=9,又由AE^2=EC\times{ED},得AE=3\sqrt{19}.
例25 如图边长为2的正三角形ABC中,D是BC上一点,DF⊥AC于F,在BA延长线上取一点G,使得AG=CD,连DG交AC于E,则EF= 。
解法一:(特殊位置法)
令D与B重合。则F是AC之中点,E与A重合,故EF=1.
解法二:
作DM∥AB,则易证△CDM为正三角形,且△DME≌△CAE,
故MF=\frac{1}{2}MC,ME=\frac{1}{2}MA,因此EF=\frac{1}{2}AC=1。