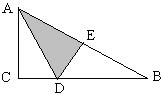
10、如图,Rt△ABC中,∠C=90°,AC=6,BC=8,D在BC上,沿AD折叠使C落在AB上的E处,求DE的长。
2011届初二王峥嵘的解法:
设CD=DE=x,由面积关系得\frac{1}{2}\times6x+\frac{1}{2}\times10x=\frac{1}{2}\times6\times8,
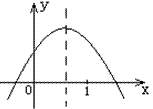
11、已知二次函数y=ax^2+bx+c的图象如图所示,则下列代数式……,a+b中,其值为负数的有 个。
2011届初三6班桑晨的解法:
a+b=(a+b+c)-c=f(1)-f(0),从图象中可见,x=1的函数值比x=0时函数值大,所以a+b>0.
12、如图,已知D、E分别在△ABC的边AB、AC上,且DE∥BC,AB=4,AC=3,BC=5。当△ADE的周长与四边形DBCE的周长相等时,求DE的长。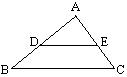
2011届初三2班范家琦的解法:
设DE=x,∵DE∥BC,∴△ADE∽△ABC,∴\frac{C_{\triangle{ADE}}}{C_{\triangle{ABC}}}=\frac{x}{5},即C_{\triangle{ADE}}=\frac{12}{5}x,∵△ADE的周长+四边形DBCE的周长=△ABC的周长+2DE,∴2\times\frac{12}{5}x=12+2x,解得x=\frac{30}{7}.
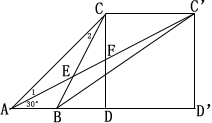
13、如图,两个观察者从A、B两地观察空中C处一个气球,分别测得仰角为45°和60°,已知A、B两地相距100m,当气球沿与AB平行的路线飘移20秒至C’,在A处测得气球的仰角为30°。求:
(1)气球飘移的平均速度(结果保留3个有效数字);
(2)在B处观察点C’的仰角(精确到1’)。
2011届初三2班李景的解法:
(1)由已知,∠1=∠2=15°,所以AE=CE,
又∠EAB=∠ECF=30°及对顶角相等,∴△EAB≌△ECF,∴CF=AB=100,
∵\angle{FC{^\prime}C}=30°,\angle{C{^\prime}CF}=90°,∴CC{^\prime}=\sqrt{3}CF=100\sqrt{3},
∴移动速度v=\frac{100\sqrt{3}}{20}≈8.66(m/s)。
(2)∵∠AEB=∠CBD-∠EAB=60°-30°=30°,∴BE=AB=100,
∵AB:BE:AE=1:1:\sqrt{3},
∴AE=CE=100\sqrt{3},
CB=BE+EC=100+100\sqrt{3},
∴BD=50+50\sqrt{3},
BD{^\prime}=50+50\sqrt{3}+100\sqrt{3}=50+150\sqrt{3},
C{^\prime}D{^\prime}=CD=\sqrt{3}(50+50\sqrt{3})=50\sqrt{3}+150,
∴\angle{C{^\prime}BD{^\prime}}=tan^{-1}\frac{50\sqrt{3}+150}{50+150\sqrt{3}}≈37°22’。
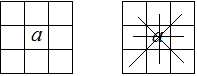
14、将1至9这九个数字填入3×3的九宫格,使得每行、每列、每条对角线上的三个数之和都相等。问最中间的数字是什么?为什么?
1011届六年级许紫欣的解法:
∵三个横行的和=1+2+3+……+9=45,∴每个和=45÷3=15,
如图,设中间数为a,那么上图4条线的4个和等于将1到9加遍后又多加了3个a,
所以有:4×15=45+3a,a=5.
15、如图,抛物线y=2x^2-\frac{5}{2}x+a与x轴正半轴交于A、B两点(A在B的左边),与y轴正半轴交于C,且∠OCA=∠OBC,则B点坐标是 ( )
A、(\frac{1}{4},0) B、(4,0) C、(1,0) D、(3\sqrt{3},0)
2011届初三6班桑晨的解法:
此抛物线的对称轴是直线x=\frac{5}{8},如图,利用对称性知,B点的横坐标介于\frac{5}{8}和\frac{5}{4}之间,只有C符合。
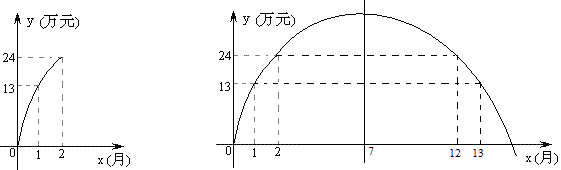
16、一家电脑公司推出一款新型电脑,投放市场以来,前两个月的利润情况如图所示,该图可以近似地看作抛物线的一部分,其中第x月的利润为y万元,往后y与x满足的关系不变.请结合图象解答下列问题:
(1)求抛物线对应的二次函数解析式;
(2)该公司在经营此款电脑的过程中,第几月的利润最大?最大利润是多少?
(3)公司打算,从月利润下降开始,若后一个月与前一个月利润之差超过11万元,就停止销售该产品,请你预测该产品持续销售的时间.
2011届初三6班桑晨的解法:
(1)y=-x^2+14x;
(2)当x=7时最大利润为49万元;
(3)如上右图,根据抛物线的对称性可知,第12月到13月利润刚好下降11万元,所以持续销售时间是13个月。
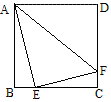
17、如图正方形ABCD中,点E、F分别在边BC、CD上,若AE=4,EF=3,AF=5,那么正方形的面积等于 ( )A、 \frac{225}{16} B、 \frac{256}{15} C、\frac{256}{17} D、\frac{289}{16}
张天行:由△ABE∽△EFC,得\frac{AB}{CE}=\frac{AE}{EF}=\frac{4}{3},设AB=x,∴EC=\frac{3}{4}x,∴BE=\frac{1}{4}x,则x^2+(\frac{1}{4}x)^2=4^2,解得x^2=\frac{256}{17},即为正方形的面积。
桑晨:由△ABE∽△EFC,得\frac{AB}{CE}=\frac{AE}{EF}=\frac{4}{3},设AB=x,∴EC=\frac{3}{4}x,而BE=\sqrt{4^2-x^2},由BE+EC=AB得\sqrt{4^2-x^2}+\frac{3}{4}x=x,也解得x^2=\frac{256}{17},即为正方形的面积。
王嘉宁:设BE=a,EC=b,则AB=a+b,于是\left\{\begin{matrix} \frac{a+b}{b}=\frac{4}{3}\\(a+b)^2+a^2=4^2\end{matrix}\right.
由①得b=3a,代入②得a^2=\frac{16}{17},再代入②得(a+b)^2=\frac{256}{17},即为正方形的面积。
18、如图,C、D是以AB为直径的半圆O上两点,CE⊥AB于E,DF⊥AB于F,DG⊥OC于G,求证:CE=GF。
2011届初三王宁的解法:
如图连OD,分别以CO、DO为直径作辅助圆,可以证明圆过E和G,F,
容易证明∠COE=∠GDF,又因为这两个圆是等圆,所以CE=GF。
以下内容转至《学生妙解数学题3》
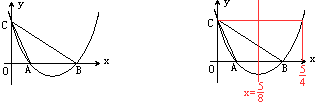
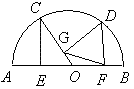
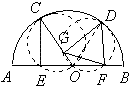
学生的解法很妙,但更值得尊敬的是象你这样关爱学生做法的老师,佩服佩服!
不错,我应该好好学习