前面已经有很多学生妙解的例子了(共18题),具体的见:
自从我留心学生巧妙的解法,真的对学生有了新的认识:人的能力不可小视,一切皆有可能!有兴趣的你点进去看看,保证你拍案叫好。
今另起一文,再陆续摘录我学生的妙解。
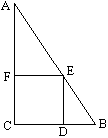
19、如图,直角三角形ABC中,∠C=90°,AC=8,BC=6,正方形CDEF的顶点D、E、F在三角形的边上,求正方形的边长。
学生一的解法:
设正方形的边长为x,因为图中三部分的面积之和=总面积,
所以 \frac{x(8-x)}{2}+x^2+\frac{x(6-x)}{2}=\frac{6{\times}8}{2},解得 x=\frac{24}{7}。
学生二的解法:
如下图,连CE,\because S_{\bigtriangleup{AEC}}+S_{\bigtriangleup{BEC}}=S_{\bigtriangleup{ABC}}
\therefore \frac{8x}{2}+\frac{6x}{2}=\frac{6{\times}8}{2},解得 x=\frac{24}{7}。
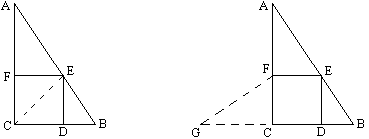
学生三(2013届初一冯嘉昊)的解法:
将△AEF割下拼到△GFC的位置,那么图中的关系是:梯形的面积=原三角形的面积
\therefore \frac{1}{2}[x+(8-x)+6]x=\frac{6{\times}8}{2},解得 x=\frac{24}{7}。
点评:这三位同学都用面积法解题,都运用了方程思想,一个方法、一个思想在同一个问题中得到了体现,真是难能可贵啊。
20、如图,梯形ABCD中,AC=CB,AC⊥CB,∠D=∠DAB=Rt∠,∠ABC的平分线交AD于E,交AC于G,EF⊥AC于F,求证:S_{\bigtriangleup{EFG}}:S_{\bigtriangleup{AEG}}=EG:EB。
学生一的解法:
可以算出∠AGE=∠AEG=67.5°,所以AE=AG,且Rt△EFG∽Rt△BAE,
所以S_{\bigtriangleup{EFG}}:S_{\bigtriangleup{AEG}}=GF:GA=GF:EA=EG:EB。
学生二(2011届初三2班袁佳琦)的解法:
作GH⊥AB于H,设EF=1,则AG=AE=\sqrt{2}
所以S_{\bigtriangleup{EFG}}:S_{\bigtriangleup{AEG}}=GF:GA=(\sqrt{2}-1):\sqrt{2}。
又△AEF≌△AGH,所以GH=EF,
∴EG:GB=FG:GC=FG:GH=FG:EF=(\sqrt{2}-1):1,
∴EG:EB=(\sqrt{2}-1):\sqrt{2},即S_{\bigtriangleup{EFG}}:S_{\bigtriangleup{AEG}}=EG:EB。
21、如图14,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?
第(1)小题略
解第(2)小题时,我们常常如图作CE⊥BD于E,利用三角函数或方程解决问题,但会比较麻烦。
2011届初三王峥嵘和林甬开的解法是:
如图作AF⊥BC于F,则容易得∠FPA=75°,∠C=45°,在△ABF中,因为∠B=30°,
∴AF=\frac{1}{2}AB=\frac{1}{2}(10+10\sqrt{3})=5+5\sqrt{3}.
∴AC=\sqrt{2}AF=\sqrt{2}(5+5\sqrt{3})=5\sqrt{2}+5\sqrt{6}.
22、如图,正△AOB中,点O是坐标原点,AO=2,∠AOx=45°,求点B的坐标。
2012届初二王佳露的解法:
如图,作AC⊥x轴于C,BD⊥x轴于D,连BC,由已知得,四边形ABOC是以BC为对称轴的轴对称图形,∴AO⊥BC。
所以BE=\sqrt{3},EC=1,
因为△BDC是等腰直角三角形,所以BD=\frac{BC}{\sqrt{2}}=\frac{\sqrt{3}+1}{\sqrt{2}}=\frac{\sqrt{6}+\sqrt{2}}{2}.
OD=\frac{\sqrt{6}-\sqrt{2}}{2}.
B点坐标为(\frac{\sqrt{6}+\sqrt{2}}{2},\frac{\sqrt{2}-\sqrt{6}}{2})
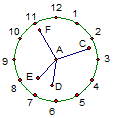
23、小明开始做作业时,时针在6、7之间,时针和分针的夹角110°,做完作业时,时针还在6、7之间,时针和分针的夹角仍是110°,问小明做作业的时间是多少分?
2013届初一8班周喆旻的解法:
如图,设小明做作业的时间是x分,分针由AC走到AF,时针由AD走到AE。
我们知道,分针每分钟走6°,时针每分钟走0.5°,那么∠EAD=0.5x,
于是2×110+0.5x=6x,解之x=40. 答:小明做作业的时间是40分.
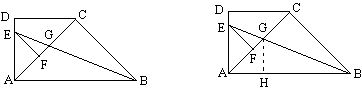

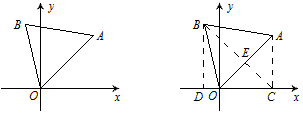
我要学习
方法真多啊!!!!