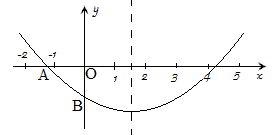2013年2月6日下午1:30在宁波市大学园区图书馆（宁波中学附近，鄞州区学府1号旁边），由江东区初中数学教研员潘小梅老师主讲《初三数学怎样迎考》，也会从命题者的角度剖析个别江东期末考试题。欢迎初三学生参加。
运用极端原理居然错了
学生练习中有一道二次函数应用题：
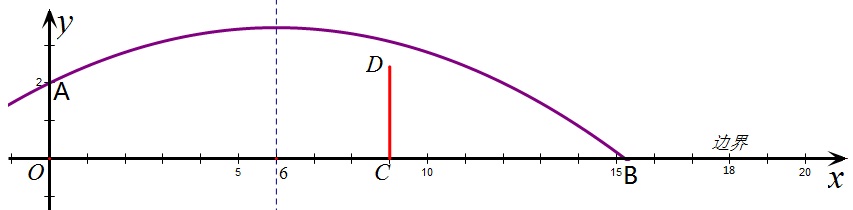
（安徽2012年）23.如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x(m)满足关系式y=a(x-6)^2+h.已知球网CD与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m。
（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求h的取值范围。
本题有3个小题，前2个小题略。
我做第（3）题的方法是采用极端原理。
解：当抛物线过D点时，可以将A（0,2）及D（9,2.43）代入，得
\begin{cases} 36a+h=2\\ 9a+h=2.43 \end{cases}，解得\begin{cases} a=-\frac{43}{2700}\\ h=\frac{193}{75} \end{cases}，
当抛物线过边界（18,0）时，可以将A（0,2）及B（18,0）代入，得
\begin{cases} 36a+h=2\\ 144a+h=0 \end{cases}，解得\begin{cases} a=-\frac{1}{54}\\ h=\frac{8}{3} \end{cases}，
因为\frac{8}{3}>\frac{193}{75}，所以\frac{193}{75}\le{h}\le\frac{8}{3}.
初中几何所有的公理及其定理、推论（转）
1 .过两点有且只有一条直线
2 .两点之间线段最短
3. 同角或等角的补角相等
4 .同角或等角的余角相等
5 .过一点有且只有一条直线和已知直线垂直
6 .直线外一点与直线上各点连接的所有线段中，垂线段最短
自编抛物线难题解答
关于x的二次函数y=ax^2+bx+c图象如图所示。
（1）判断c-4b的符号；（2）判断a-2b+4c的符号；（3）如果OA=OB，求证：0<a<1.
解（1）
由\frac{b}{-2a}>1，得b<-2a，即-2b>4a，
∴c-4b=-2b-2b+c>4a-2b+c=f(-2)>0.
（2）
a-2b+4c=4(\frac{1}{4}a-\frac{1}{2}b+c)=4f(-\frac{1}{2})<0.
（3）
∵OA=OB，B点坐标为（0，c），∴A点坐标为（c，0），
∴ac^2+bc+c=0，ac+b+1=0，
∵f(1)<0，即a+b+c<0，∴b<-a-c，
∴ac-a-c+1>0，即(a-1)(c-1)>0，
∵c-1<0，∴a-1<0，即0<a<1.
自编一道抛物线难题，请你来挑战。
今天上课的内容是复习二次函数，我随手编了一道题，学生只会做第（1）题，现拿出来与大家共享，并考考你。如果你在下面评论里写出了正确的解答，将会获得一套初三培优试卷作为你的奖励。
关于x的二次函数y=ax^2+bx+c图象如图所示。
（1）判断c-4b的符号；（2）判断a-2b+4c的符号；（3）如果OA=OB，求证：0<a<1.
奇妙的抛物线
作为初中数学教师，最难能可贵的是发现数学中的新的结论。在2012年的中考试题中，这样的新发现有很多很多，我特佩服这些命题的专家，他们太伟大了。
过去，我惊奇地发现：所有抛物线都相似的。
我在做2012年天津中考数学试卷26题时，发现了如下的结论： 继续阅读“奇妙的抛物线”
黄金分割点
在学习相似三角形时，必定会学习黄金分割点和黄金比的概念。
一次，郑瑄老师要去省里上一节展示课，内容正好是黄金分割。她如约来听了我的这节课，课后她对我的课指出了一些优点和缺点，并提出了自己的教学设计，要我帮她计划计划。我当时傻呆了，因为我是第一次听说这节课可以这样上。
几天后我有幸听到了郑老师精心设计的《黄金分割》课，听课者达60人之多，课后大家都认为教学如此新颖、设计那么大胆。
下面根据我的听课笔记，向大家作一个展示。
△在解决数学问题中的作用
△指的是一个二次三项式ax^2+bx+c中b^2-4ac的值，这个代数式有着广泛的应用。
1、判别一元二次方程根的情况
2、判别二次三项式是不是完全平方式
3、判别二次三项式在实数范围内是不是可以分解因式
4、判别二次函数与x轴公共点的个数
5、判别一元二次不等式解的情况
6、判别二次三项式的符号
7、求分式的最值
具体说明如下。
中考禁用计算器说明什么？
宁波市教育局规定，2013年所有学科中考禁用计算器。
一霎那，褒贬不一的声音响起。
有称道的说：是要禁止，学生的计算能力实在太差了。
有抱怨的说：那也太急了，不能体现公平性。
三门问题
三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。
参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机会率？
这一问题的关键在于主持人，因为他总会挑一扇后面没有奖品（汽车）的门。游戏秀的调查数据显示，那些改选的参赛选手赢的几率是那些没有改选的人的两倍，这证实了莎凡特在其第三篇专栏中的解释：“当你从三扇门中选了门1后，这扇门后面有奖的几率是\frac{1}{3}，另两扇门是\frac{2}{3}.但接下来主持人给了你一个线索。如果奖品在门2后，主持人将会打开门3；如果奖品在门3后，他会打开门2。所以如果你改选的话，只要奖品在门2或门3后你就会赢，两种情况你都会赢！但是如果你不改选，只有当奖品在门1后你才会赢。”
按照这样推理，换门获奖的概率是\frac{2}{3}，不换门获奖的概率是\frac{1}{3}，也就是换比不换好。
但我们又想，反正打开了一扇没汽车的门，留下的2扇门中一扇有汽车，一扇没汽车，换与不换中奖的概率是\frac{1}{2}。
亲爱的读者，你认为换门获奖概率大还是不换的概率大？