作为初中数学教师,最难能可贵的是发现数学中的新的结论。在2012年的中考试题中,这样的新发现有很多很多,我特佩服这些命题的专家,他们太伟大了。
过去,我惊奇地发现:所有抛物线都相似的。
我在做2012年天津中考数学试卷26题时,发现了如下的结论:
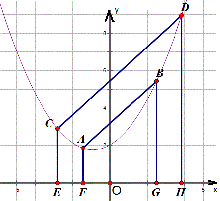
如图,对于任意的一条抛物线y=ax^2+bx+c,作任意两条平行线AB∥CD,交抛物线于A,B,C,D,过这四点作x轴的垂线垂足分别为E,F,G,H。求证:EF=GH。
证明:设A(x_A,a),B(x_B,b),C(x_C,c),D(x_D,d),那么A,B,C,D的纵坐标分别为
ax_A^2+bx_A+c,ax_B^2+bx_B+c,ax_C^2+bx_C+c,ax_D^2+bx_D+c,
由于平行,所以两条直线的k相等(即斜率相等),
即\dfrac{ax_A^2+bx_A-ax_B^2-bx_B}{x_A-x_B}=\dfrac{ax_C^2+bx_C-ax_D^2-bx_D}{x_C-x_D},
所以a(x_A+x_B)+b=a(x_C+x_D)+b,即x_D-x_B=x_C-x_A,也即EF=GH。
思考:如果过A,B,C,D作y轴的垂线,垂足分别为E,F,G,H,是否还有EF=GH?这个问题留给大家。
黑马在QQ群里公布了他的发现:
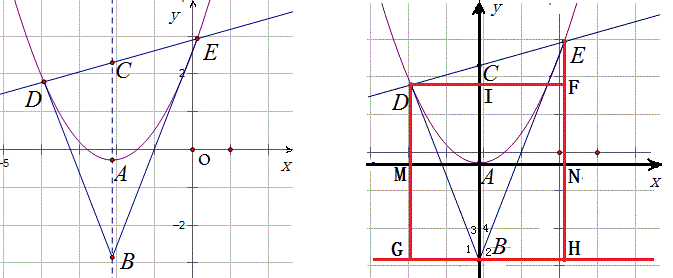
如图,对于任意的一条抛物线y=ax^2+bx+c,A为顶点,过A作x轴垂线,在其上取B,C两点使AC=AB,过C任作一条直线交抛物线于D,E两点,连BD,BE,求证:∠DBC=∠EBC。
解:如图将抛物线平移至y=ax^2的形式,这样一切几何性质不改变。添上如图红色的辅助线。
设D(x_1,ax_1^2),E(x_2,ax_2^2),那么由CI∥EF得\dfrac{CI}{EF}=\dfrac{DI}{DF}
即\dfrac{CI}{ax_2^2-ax_1^2}=\dfrac{-x_1}{x_2-x_1},得CI=-ax_1(x_1+x_2),
CA=CI+IA=-ax_1(x_1+x_2)+ax_1^2=-ax_1x_2,
∴\dfrac{DG}{GB}=\dfrac{-ax_1x_2+ax_1^2}{-x_1}=ax_2-ax_1,
\dfrac{EH}{BH}=\dfrac{-ax_1x_2+ax_2^2}{x_2}=ax_2-ax_1,
∴\dfrac{DG}{GB}=\dfrac{EH}{BH},故△DGB∽△EHB,∴∠1=∠2,∴∠3=∠4.
不可思议的结论!一般的抛物线,一般的直线,居然有这么好的结论,当时我有点不信,在几何画板中操作了一下,终于看到了结论是对的,这时,我不禁感叹:见证奇迹的时刻到了!