定义:如果两条形如y=ax^2+bx+c(a\ne0)的抛物线二次项系数相等,那么在不同坐标系中这两条抛物线称为相似抛物线。(坐标系的横、纵坐标轴的单位长度相等)
根据这个定义,我们可以判定抛物线y=a_1x^2+b_1x+c_1(a_1\ne0)与抛物线y=a_2x^2+b_2x+c_2(a_2\ne0)是相似的。
事实上,函数y=f(x)的图象在坐标系中经过坐标变换\left\{\begin{matrix} x=kx{}'\\ y=ky{}' \end{matrix}\right.,可以得到一条和原图象相似的函数图象y^\prime=\frac{f(kx^\prime)}{k},于是我们把坐标变换\left\{\begin{matrix} x=kx{}'\\ y=ky{}' \end{matrix}\right.叫做相似变换或缩放变换。
另一方面,抛物线y=mx^2+b_1x+c_1(m\ne0)与抛物线y=mx^2+b_2x+c_2(m\ne0)的二次项系数相等,所以在不同的坐标系中它们是相似的。
于是,经过变换\left\{\begin{matrix} x=kx{}'\\ y=ky{}' \end{matrix}\right.,抛物线y=a_1x^2+b_1x+c_1(a_1\ne0)将变为ky^\prime=a_1(kx^\prime)^2+b_1kx^\prime+c_1,变形即得y^\prime=ka_1{x^\prime}^2+b_1x^\prime+\frac{c_1}{k}。所以,只要令ka_1=a_2,即k=\frac{a_2}{a_1},抛物线y=a_1x^2+b_1x+c_1(a_1\ne0)经过变换后与抛物线y=a_2x^2+b_2x+c_2(a_2\ne0)的二次项系数就相等了,也就相似了。这就证明了抛物线y=a_1x^2+b_1x+c_1(a_1\ne0)与抛物线y=a_2x^2+b_2x+c_2(a_2\ne0)是相似的。
既然所有的抛物线都相似,也就是形状相同,那么浙教版数学九年级上第35页作业题5就有问题了。
作业题5:已知一个二次函数图象的形状与抛物线y=4x^2相同,它的顶点坐标是(2,4),求该二次函数的解析式。
本题的问题就在于“两条抛物线的形状相同”,当我们知道任何抛物线的形状都相似后,这个“条件”就不是条件了。但是,类似的问题不仅仅在浙教版的教科书中,普遍存在于其他教科书、试题和教辅材料中。
如果将上述问题中的用词稍作改动,那么问题就可以解决了,改动如下:
已知在同一坐标系中,一个二次函数y=ax^2+bx+c(a\ne0)图象与抛物线y=4x^2能重合,它的顶点坐标是(2,4),求该二次函数的解析式。
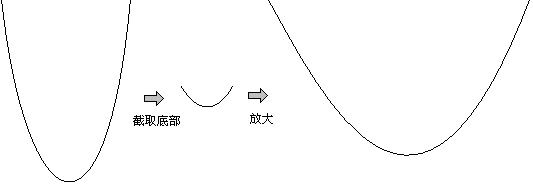
如果大家还是觉得“所有的抛物线都相似”不可信的话,请看下面图示。
由此直观地看到,不论抛物线的开口大小怎样,都是相似的。我们还可以用同样的方法证明所有抛物线(对称轴不一定平行于y轴)都相似。还可以证明双曲线y=\frac{k}{x}(k\ne0)都相似。
讲述了所有的抛物线都相似后,它的意义何在?它又有什么用处?文章没有涉及。也是我感到遗憾的地方。希望有这方面灵感的同行与我交流。
无独有偶,有人和我一样关注过同一个问题,如你有兴趣可以点击这里。
🙂 把我当老师了…呵呵,话说中国喜欢做超出课本的研究的中学老师也不多,膜拜下!
@Vilic
这位老师,你可否将你文章的链接发一下?
呵呵,今天写了一篇《神奇的抛物线》,讲得差不多,不过我是从斜抛找来的灵感。