新课引入是一节课成败的关键所在,我在以前写过《新课引入策略谈》,这儿想通过几个实例,具体地说明有些新课可以怎样引入。由于新课引入的方法各人有各自的方法,所以还望同行给出更好的方法,给予点评。
分类: 课堂教学
一段数学探究活动纪实
今天给学生讲解一道很平常的几何题:
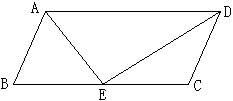
如图,平行四边形ABCD中,AD=2AB,E是BC的中点,求证:∠AED=90°.
解完后,我对同学们说:
我经常告诫大家,解题后要留有思考余地,本题我们能思考什么呢?
“考虑问题反面”是解决问题的重要方法
有时候解决问题的反面远比解决问题的正面来得简单。这是一种思想还是一种方法?我也说不清,反正很有效。生活中也有这样的做法,我常常猜想,是不是许多数学方法来自于生活?是不是许多数学思想源自于生活?这是一节我非常得意的数学专题课,我讲的专题是《从反面考虑问题》,这是一个成功的案例。
那天,狂风大作。我走进教室,习惯地带上门,可总是关不住,扫帚顶、凳子靠都不管用,学生似乎在笑。
学生的能力不可低估
文章摘要:
我们教师往往低估了自己学生的能力,有时候在不经意中却发现学生在作业中给出的答案、在提问时给出的回答、在讨论中侃出的结论、在讲台上表现出的老练……,这些都会给我们以很大的惊奇。惊奇之余我们一定会静下心来思索,如何才能充分发挥学生的能力呢?
我作了许多次尝试,有成功的,也有失败的。本案例是一个成功的案例,故事发生在“在同一个平面内,两条直线有哪几种位置关系”的提问之后,在备课时我没有想到会有如此热烈的讨论,会有如此深入的思考!我惊奇,我反思,我要记录发生的故事,我要发泄心中的感慨,于是便有斯文。
关键字:能力 平行线 讨论 新课标
正文:
怎样用实验解决初中数学问题
“实验”不是物理、化学的专利。用实验解决数学问题,是近几年来新理念下的热门题型。这样的问题往往不需要复杂的计算和推理,只需动手操作,实验观察即可。这是对学生动手能力、想像能力和观察能力的挑战。《数学课程标准》从“基本理念”到“总体目标”再到“课程实施建议”都提出了数学实验的要求,那么教师怎样在课堂教学中落实这个要求呢?我在这方面进行了较多的尝试,下面谈谈如何用实验解决某些初中数学问题。
数学实验方法1——正确作图,仔细度量
某些几何计算题(选择题或填空题,下同),直接解有一定困难,如果按题意准确作图(甚至要用圆规),再用刻度尺或量角器或圆规进行度量比较,得到结果。
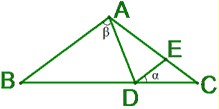
例1、如图,△ABC中,AB=AC,D在BC上,E在AC上,AD=AE,设∠EDC=α,∠BAD=β,那么α与β关系正确的是 ( )
A、β=α B、β=2α C、β=2.5α D、β=3α
实验:画图时应讲究技巧,先画∠BAD=60°,再任画射线BD,然后用圆规截取AC=AB,AE=AD,那么便可量出∠EDC=30°,故选B。
遵循学生认知规律,提高课堂教学效益
心理学的研究表明,学生在学习知识、技能的过程中遵循一定的认知规律。遵循学生的认知规律,让学生在符合自身认知规律的教学活动中成长,这样的教学才会变得更有效。
某些学校某些老师,不是设身处地为学生着想,遵循他们的认知规律,而是“二节新课一节上,没有学过先要考,个个来做竞赛题,学生都把神仙当”。尤其是一些重点中学,许多好学生就这样厌学了,身心受到极大的创伤,这种效应还波及到父母。大多数教师没有这样离谱,但还是有人对学生认知规律把握不准,教学难度、广度、深度、梯度模糊不清,教学方法、教学模式选择有误,课堂结构安排不合理,使得学生学习困难。如果我们每一个教师能转换角色,常常想一个问题:“我要是作为学生,听自己的课,哪里会有困难?”那么他一定是个好教师。
可以这样说,我的成功离不开这个想法。我读初一的时候,数学老师上课上得我云里雾里,为什么要学有理数?为什么要叫有理数?为什么要这样算有理数?种种困惑使我对数学失去学习的兴趣。我当老师的第一个承诺是:“我绝不做我初一的数学老师。” 如何遵循学生的认知规律,我的做法供大家参考。
1、讲授概念通俗易懂
初中生的心理特征和认知规律告诉我们,他们的形象思维比抽象思维更完善,抽象思维还有待于继续发展,抽象程度还不能太高。所以教师常常需要借助图形、图象、类比、举例、枚举、特殊到一般等方法进行教学,这就是为什么要在初中阶段提倡轻概念重能力的原因。
例如:
(1)直线和圆的位置关系
本课可以用类比方法来进行教学,教师先画出如下表格(右边的内容暂不列出)进行复习:
| 名称 | 三角形的外接圆 | 三角形的内切圆 |
|---|---|---|
| 定义 | 经过三角形三个顶点的圆叫做三角形的外接圆 | 和三角形三边都相切的圆叫做三角形的内切圆 |
| 圆心的名称 | 外心 | 内心 |
| 圆心的产生 | 两边中垂线的交点 | 两条角平分线的交点 |
| 性质 | 外心到三角形的三个顶点距离相等 | 内心到三角形的三边距离相等 |
然后用类比的方法逐条添加表格右边的内容。
新课引入策略谈
什么叫做创设情境?什么叫做新课引入?也许两个概念有区别,但不加区别也无妨。新课引入好不好,情境创设妙不妙,直接关系到一节新课的成败。许多教师在这点上是非常重视的,教学设计时在这里下足了“工夫”,其实也是最能体现教师的“功夫”。
我认为新课引入要遵循以下几个原则。
一、必要性
新课引入(或者说创设情境)有无必要,要根据教学内容而定。可以说大多数新课是有必要进行新课引入的,有些可以从数学问题引入,有些可以从生活实际问题引入。但有些新课却没有必要引入,可以开门见山直接开始新课的学习。
例1 学习《线段、射线和直线》、《认识三角形》、《代数式的值》等等这样内容的新课时,就没有必要创设情境了,直奔主题吧!可是有些老师却花大量的时间创设情境。如学《认识三角形》时,有老师用PPT播放了2分钟有三角形的用具、建筑物等大量图片,这个实在没有必要。
二、针对性
关注学生的思维过程是教学成败的关键
学生的思维有时候很独特,我们教师根本想不到,事后常常会有这样的感叹:“啊,还有这种想法?”、“原来是这样想的,怪不得做不出”、“嘿!这个我倒没想到”。
长期来,我经常与学生交流(主要在上课中),交流的方式是对话,我喜欢问“你是怎样想的”?而不是问:你是怎样做的,收获颇丰。逐渐,我可以做到事先预见学生的想法,猜测学生做题时会遇到怎样的困难、有几种做法、所占的比例是多少。使我能较好的把握教学的对象、难度、梯度,及时应对各种突发情况,控制教学局面。并能把这种能力迁移到其它教学领域中,如命题、编题、解题、论文、说课等。