新课引入策略谈

什么叫做创设情境?什么叫做新课引入？也许两个概念有区别，但不加区别也无妨。新课引入好不好，情境创设妙不妙，直接关系到一节新课的成败。许多教师在这点上是非常重视的，教学设计时在这里下足了“工夫”，其实也是最能体现教师的“功夫”。

我认为新课引入要遵循以下几个原则。

一、必要性

新课引入（或者说创设情境）有无必要，要根据教学内容而定。可以说大多数新课是有必要进行新课引入的，有些可以从数学问题引入，有些可以从生活实际问题引入。但有些新课却没有必要引入，可以开门见山直接开始新课的学习。

例1  学习《线段、射线和直线》、《认识三角形》、《代数式的值》等等这样内容的新课时，就没有必要创设情境了，直奔主题吧！可是有些老师却花大量的时间创设情境。如学《认识三角形》时，有老师用PPT播放了2分钟有三角形的用具、建筑物等大量图片，这个实在没有必要。

二、针对性

新课引入时选择的例子一定要服务于新课的内容，如果选用的例子与本课的内容没有关联，那么这样的引入是无效的。

例2  在一次优质课评比中，一位老师上课内容是《直角三角形复习》，一开始他在屏幕上打出电影的海报，说：这部电影还少一位演员，今天我来选演员，看你们有怎样的表演，先来规定动作。

例3  同样是例2中的这节课，另一位老师要学生剪纸折叠，她在教案里是这样写的：“以手工制作的创意引入，一张纸的裁剪拼合可以构造生活中的无数美丽和惊奇，激发学生热情，使学生怀着探索的欲望进入直角三角形的复习，用一个小小的直角三角形变出几何世界的无限精彩。”这怎么可能？从三角形折纸中能“变出几何世界的无限精彩”？我想，这“无限精彩”只有在证明、计算后才能体现！所以我认为这样引入只不过为作秀。

例4  《代数式复习》一课中，老师是这样引入的：
师：如果老师想介绍自己，你认为我会先介绍什么？
生：姓什么！
师：老师先不说，只是告诉你老师的邮箱地址：tuxubo@sina.com，你能猜出我的姓名吗？
生：……（学生尝试着拼音）
师：对了！那你知道这个邮箱地址用的是什么？
生：字母！
师：那么在我们数学中有字母吗?
生：有，代数式里有字母。
师：这节课我们就来复习“代数式”。

这样的引入与授课内容几乎没有什么联系，这是课堂教学的大忌！

三、科学性

引入的实例要与新课内容（概念、原理、性质）相符，即符合科学性，背离科学性的例子是万万不可以的。

例5  浙教版七年级下《2.2轴对称变换》一节中，用剪“双喜”的例子引入，这在科学性上是有问题的。因为轴对称变换是指两个图形，一个图形是原图形，另一个是原图形的像。而“双喜”一般看作是一个图形，它是一个轴对称图形。

例6  为了《锐角三角函数》的引入，有许多老师就用梯子陡不陡，走斜坡累不累的例子，不仅科学性有问题，而且可以说与本课内容没有关系，缺乏针对性。

四、实用性（可操作性）

引入的例子可操作性越强，它的实用性就越好。否则，中看不中用没有实用性，而且还会陷入使得课堂教学无法进行的尴尬境地。

例7  多次以评委身份听了《探索勾股定理》这一课，新课引入可算得上五花八门，有些用面积引入，有些用度量引入。我认为度量有误差，不好！更有甚者，有老师干脆让学生画出一个任意的直角三角形进行度量，oh my god，这怎么收场？有一个老师让学生对已经获得的直角三角形三边3，4，5；5，12，13；6，8，10等，进行探索，希望学生发现勾股定理。晕！数学家们发现勾股定理要几百年上千年，你居然要学生一节课里就发现？根本没有可操作性。

五、实际性

千万不要以为所有新课的引入必须用生活实际例子，有些课的引入没有必要或完全不可能用生活实例。如果用了生活实例，则必须要符合实际情形，否则就会脱离实际，闹出笑话，误人子弟。

例8  某老师为了《扇形的面积》的引入，用了一个实际例子：  让我们来探究生活中有关粉刷墙壁时，刷具扫过面积的问题。某工人用的刷具形状是圆形（如图1），直径CD=20cm，点O、C、D在同一直线上，OC=30cm，他把刷具绕O点旋转90°，则刷具扫过的面积是多少cm^2？

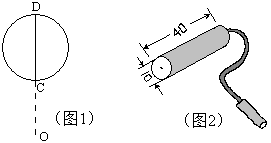
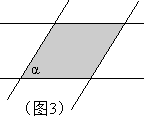
    生活中谁见过这样的刷具？我见过的刷具是如图1的样子，现实生活中的刷具是图2的样子。实际问题不实际是我们教师自身缺乏生活常识导致的，看来我们教师也要社会实践，才能获得更丰富的经验。

例9  这是一节《锐角三角函数复习课》，一位老师用下例引入：
      如图3是两条宽度都是5的交叉公路，它们的夹角为α ，则两条公路重叠部分（阴影部分）的面积是   （     ） 
          A、\frac{25}{\sin\alpha}     B、\frac{25}{\cos\alpha}     C、5{\sin\alpha}     D、\frac{5}{\tan\alpha}

这里有两个不切实际的地方。其1，四岔路口的转角处不会是尖角，而是带弧状的。其2，宽度为5，没有单位，而且5米太小，5千米太大。

六、新颖性

以新颖的实例作为新课的引入，会让人耳目一新，有一种新鲜感。下面每例都用两种方法引入，请读者对比、体会。

例10  代数式复习课的引入

 方法1：

我们能用代数式简明地表示一些数学规律，例如加法交换律a+b=b+a，乘法分配律a(b+c)=ab+ac，梯形面积公式S=\frac{(a+b)h}{2}。

方法2：

同学们，认识他吗？魔术大师刘谦，还有他的扑克牌。今天，老师也想学学刘谦，给大家玩一个数学小魔术。现在，我手中有一副扑克牌，共54张，去掉大小王，共52张。我把52张扑克牌分成2堆，一堆是一位数，一堆是两位数，其中“J”代表11，“K”代表13。现在，老师需要3位助手。好，我们就请前排的两位同学上来帮忙！你们两位各拿一堆牌，各自洗牌，然后牌面朝向观众展开。第三位同学按照屏幕的步骤操作（老师读，抽签的学生操作并计算）。
     屏幕显示：
    从两位数的一堆中任抽一张牌，把这个数乘以2；得到的积 加上10；得到的和 乘以5；再从一位数的一堆中任抽一张牌，加上前面得到的数。现在请你把得到的结果告诉大家，同学们，你们知道这两张扑克牌表示的数吗？ 

例11  浙教版八年级上《由三视图描述几何体》的引入

方法1：

你能从下面所给的三视图中推断出它们分别表示什么几何体吗

 

    这样的引入与教材中一模一样。

方法2：

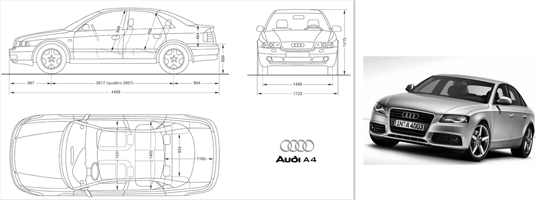
同学们，  你知道汽车模型是怎样画出来的？是用电脑3D软件根据三视图画的，下面就是奥迪A4的三视图和3D效果图。

除了上面提到的6个原则外，新课引入还要注意前后呼应，即提出的问题可以不马上解决，而是放在末尾。另外引入要自然，不要牵强附会。如果一个老师能收集好的引入，必将收获颇丰，我相信只要做个教学上的有心人，自己也能设计出精彩的引入，这是教师和学生双赢的好事。

因我徒弟要求，我会在以后日子写一篇文章，它包含我最喜欢的新课引入，题目是《新课引入集锦》，希大家稍等。