学好数学，学会做人

学会做人不仅仅是爱国、公德、人格、品质，还有更多的内容，刚强的毅力、灵活的方法、缜密的态度、创新的举动，而这些正是数学学习的重要内容，也是我们数学教师在教学中渗透德育教育的好机会。

据调查，在我们宁波市的校级领导人中，数学出身的比例最高，而且高得很多，这与数学的特殊功能—-“学会做人”是分不开的。

数学是锻炼思维的体操，培养能力的运动，学会做人的集训。初中数学与“学会做人”到底有多大关系呢？关系很大！有些学生不会解数学题，不是因为缺少数学知识，也不是缺少数学能力，而是缺少人的一种品质，缺少一种胆量、谋略和理念。甚至是某种人格的缺失。你可能会质疑：有这么严重吗？

有些人学不好数学，和他的性格很有关系，某种性格的人这辈子是不可能学好数学的，除非改性格，但是江山易改，本性难移。或者靠那些“能让猪猪开飞机”的老师进行题海战术，机械的重复，死板的记忆，获得暂时的成绩，这些人到了高中学好数学依然是不可能的。

这里我想说，“能让猪猪开飞机”的老师是教育界的罪人，因为你将毫无学习能力的人硬生生地塞进了重点高中，而排挤了那些各种能力超群、学习成绩欠佳的学生。这是教育界的杯具，是中国的杯具。

为了使大家看到数学与做人的关系，先看看学会做人到底还涉及哪些内容。

• 反面思考 ：生活工作都需要反面考虑问题，才能起到事半功倍的效果。例如大风天关不住门，可以先关窗；要交一个朋友，可以先反对他的敌人。
• 锻炼胆魄：没有胆略谋不成大事，没有胆魄干不成大事。
• 心想事成：心想事才成，异想天能开。
• 学会利用：当今社会互相利用是一种手段。没有这种手段的人，做任何事都要另辟蹊径，这种人被视为缺少办事能力。
• 选择方法 ：会选择合理方法的人，做事总是事半功倍的。
• 按部就班：有计划、有步骤地做事和毫无头绪的瞎做，是体现了两种不同人的处世观
• 热爱生活 ：只有热爱生活的人才是乐观的，只有热爱生活的人才会继续追求更好的生活。
• 打破常规：墨守陈规，无所作为。马克思主义活的灵魂是什么？马克思主义哲学的一条基本原则是什么？对了，具体问题具体分析。不能一概而论，不能一刀切。
• 学会模仿 ：从幼儿园开始，小朋友在老师的指导下进行模仿。“请你跟我这样做，我就跟你这样做”是幼儿园最常见的游戏。在工作和生活中，模仿可以直接或间接地借用别人或自己的经验。
• 细心细致：细微之处见精神，仔细认真才能办好事。
• 知难而退：“明知山有虎，偏向虎山行”这是有勇无谋的表现。知难而退，另辟蹊径，是明智的选择。
• 预见未来：做一件事情前先预见可能的结果，做这一步预见下一步，这是一个人做事的基本准则。这里既有推理能力问题，也有思考习惯问题。
• 避难就易：有几件事情等待你做，你应该先做容易的，再做难的。
• 旁门左道：有时常规的方法很难解决问题，有时走正道的能力不够，你不妨走旁门左道，这似乎是不正当手段，只要能解决问题，只要不违法，黑猫白猫都是好猫。

以上做人的内容在数学学习中是一致的，只是我们有时没有及时把握。下面我用具体的例子来说明数学教学中是怎样培养学生这些能力的。

一、反面思考

我在以前写过《“考虑问题反面”是解决问题的重要方法》。所以在这儿就不再举例。

二、锻炼胆魄

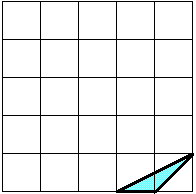
例1  在5×5的正方形网格中已有一个三角形，请你在其中画出一个最大的格点三角形，使它与已有的三角形相似。

做这道题就可以分出两种人来，一种做法是：将原三角形的边长扩大2倍或\sqrt{5}倍，以为这样得到的三角形最大了。另一种是：在网格中画一条最长的线段（对角线）作为三角形的最大边，再分析一下其余两边怎样画。前者缺乏胆量，后者虽然有点风险，但成功的希望很大，就算失败，也可以及时调整，今后适合于搞投资、企业什么的。

三、心想事成

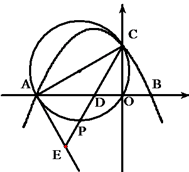
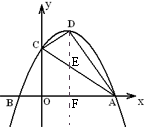
例2  如图，抛物线y=-\frac{\sqrt{3}}{3}(x+3)(x-1)与x轴交于A、B，与y轴交于C，过A,C,O作圆，E在第三象限，CE交x轴于D，交劣弧AO于P， DE=2，当P在何处时AE是圆的切线？

由抛物线的解析式可知，AO=3，CO=\sqrt{3}，要使AE是圆的切线，就必须AE⊥AC。

由ED=2，是否会有AD=2，△AED是正三角形呢？如果是的话，就有OD=1，∠ACE=∠OCE=30°，于是P为弧AO之中点。

上面的猜想是否会“心想事成”呢？这个证明其实不难。事实上，由P为弧AO之中点，可得∠ACE=∠OCE=30°，也就易证△AED是正三角形，故AE⊥AC，所以AE是圆的切线。

由以上的分析可知，数学上的一切猜想，均是“心想事成”的前提。另外，数学中的转化思想也有同样情况。请看下例。

例3  如图，已知圆O和直线l上一点A，求作圆P，使圆P与圆O外切，且与直线l相切于A。

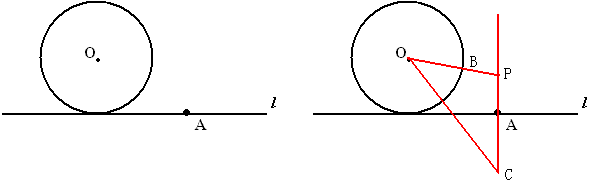分析：P点一定在过A点垂直于l的直线上。如果连结OP交圆O于B，则有PB=PA，故P在AB的中垂线上。

因为P点不确定，故B点也不确定，就很难用中垂线来产生P点。

能否将问题转化为P到两个定点的距离相等呢？如果能，两个定点在何处？

这似乎有点“异想天开”，但问题常常就是被这样异想天开的人解决的。

我们可以这样想，可否在直线l的下方找一点C，使PC=PO？这个不难，只要取AC等于圆O的半径即可。

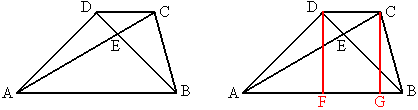
例4  如图梯形ABCD中，DC∥AB，AD和DB垂直且相等，AC=AB，对角线交于E，求证：BC=BE。

分析：有一种灵感叫做感觉，你是否感觉到了任何人画这个图，都会相似的。这就是说此图的任何角的度数是固定的。

现在要证的是BC=BE，当然想到证∠ECB=∠CEB，会不会这两个角度都可以求出来？其实只要求其中一个就可以了，或者求∠CAB也行。

又异想天开了，这可能吗？

如果添上梯形最常用的辅助线—-两条高，我想一定能心想事成了。

四、学会利用

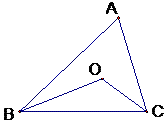
例5  如图，△ABC中OB、OC分别平分∠ABC和∠ACB。（1）设∠BAC=x度，∠BOC=y度， 求y关于x的函数解析式；（2） 请你猜想∠BOC一定是什么角？并证明你的猜想。

 

分析：解答第（1）题后，有些人就另起炉灶解第（2）题，这就是不会利用的表现。事实上，当我们求出y=90+\frac{1}{2}x后，利用这个解析式的特点，可以说明90<y<180，所以∠BOC一定是钝角。

五、选择方法

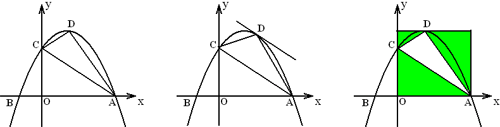
例6  如图，抛物线交x轴于A(3,0)，B(-1,0)，交y轴于C(0,2)，在第一象限内的抛物线上是否存在一点D，使△ACD的面积最大？如果有，请求出D的坐标；如果没有，请说明理由。

分析：解题和做事一样，做之前先想好几种方法，再仔细推敲哪一种方法更好。本题有三种方法选择：

1、如图，作平行于AC的抛物线切线，设为y=kx+b，其中k由AC确定，再由△=0解出b，进而可以算出D点的坐标。这种方法计算量很大。

2、如图，将△ACD的面积看做是矩形减去绿色三角形面积，写出面积关于D点横坐标的函数解析式。但是这种方法是有问题的，当D点低于C点时，图形就不是这样了。

3、如图，过D点作x轴的垂线交AC于E，交x轴于F，那么S=\frac{1}{2}DE\times{AO}.

2011年宁波市数学中考压轴题就有类似的问题，如果平时注重方法的选择，考试时就不会手忙脚乱了。

六、按部就班

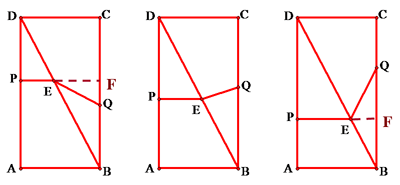
例7  如图，矩形ABCD中，AB=4，AD=8，P在AD上，Q在BC上，DP=BQ=t，PE⊥AD交BD于E，当△BEQ为等腰三角形时，求t的值。

做这样的题，要教育学生“按部就班”地进行。先要画出等腰三角形的三种不同的情形，再对每一种情形分析如何列出有关线段的代数式，然后列出关于t的方程，解完方程要检验所得的根是否符合这个情形。这是常规的过程，按部就班，老老实实是每个人正确的处世观。

如图1，当QE=QB时，EQ=t，FQ=8-2t，EF=2-PE=2-\frac{1}{2}t，然后利用勾股定理列出方程。

如图2，当BQ=BE时，DP=t，PE=\frac{1}{2}t，DE=4\sqrt{5}-t，然后利用勾股定理列出方程。

如图3，当EQ=EB时，BQ=t，FB=PA=8-t，由BF=\frac{1}{2}BQ可以列出方程。

七、热爱生活

生活中有数学，数学可以解决生活问题。如果学生能够在学习数学中热爱生活，这必将是数学教育的最高宗旨之一，是造福人类的千秋伟业，是功德无量的造化。

例8  下面的生活问题都可以编出有趣的数学题，题目略。

八、打破常规

解数学题可以看出一个人是否有创新的思维、创新的举动。习惯的做法未必是好方法，常规的、传统的做法未必是是好方法。

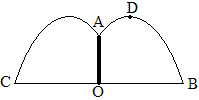
例9  如图，某公园要建造一个圆形喷水池，在水池中央垂直于水面竖一根柱子，上面的A处安装一个喷头向外喷水。连喷头在内，柱高为0.8米，水流在各个方向上沿形状相同的抛物线路径落下（如图），水流最高点距离水面1.8米，距离柱子水平距离1米。如果不计其它因素，那么为了喷出的水都落在池内，水池的直径至少为  （    ）

A、(2+\frac{6}{5}\sqrt{5})米        B、(3+\frac{2}{5}\sqrt{5})米     C、4米      D、3.8米

常规的做法是，先建立以O为原点的坐标系，求出第一象限内的解析式，再求出B的坐标。这样做计算量较大，毕竟是一道选择题，我们可以创新一下，不需要建立坐标系，也不求解析式，但可以看出答案是哪个。

事实上D点横坐标是1，利用抛物线的对称性，所以OB>2，BC>4，在4个选项中大于4的只有A。

例10  有一些按规律排列的等式：
第1个：1^2+3^2=10，
第2个：3^2+5^2=34，
第3个：5^2+7^2=74，
第4个：7^2+9^2=130，
第n个等式是▁▁▁▁▁▁▁▁▁▁▁。

分析：常规的思路是，发现左右两边的规律，按规律写出第n个等式。但右边的规律不好找，咋办？来点创新嘛！找一种别的方法，一种自己从未使用过的方法，什么方法呢？

先写出左边是(2n-1)^2+(2n+1)^2，右边既然规律不好找就别找了，将左边算一算即可，左边=8n^2+2，

故第n个等式是(2n-1)^2+(2n+1)^2=8n^2+2，

九、学会模仿

模仿能力是学习的重要能力，任何学习都是从模仿到自创的。模仿还有第二层意思，即类比。类比即类似的比较，与老问题、旧知识比较，从而解决新问题、新知识。下面举例说明类比思想是如何运用的。

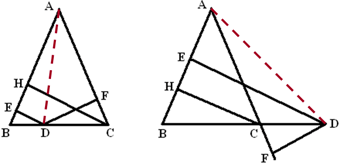
例11  如图，D是等腰三角形ABC的底边BC所在直线上一点，DE⊥AB于E，DF⊥AC于F，CH是△ABC的高。

（1）当D在线段BC上时，求证：DE+DF=CH.

（2）当D在线段BC延长线上时，（1）中的结论是否依然成立？如果成立给出证明；如果不成立，写出新的关系，并给出证明。

（1）连结AD，

∵S_{\triangle{ABD}}+S_{\triangle{ADC}}=S_{\triangle{ABC}}，

∴AB×DE÷2 + AC×DF÷2 = AB×CH÷2，∵AB=AC，∴DE + DF = CH.

（2）分析：一个点从线段上变为延长线上，其结论应该是类似的，证明过程是可以模仿的。

事实上只要将上述过程中的“+”改为“-”，就是本问题的过程了。

十、细心细致

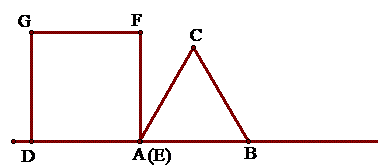
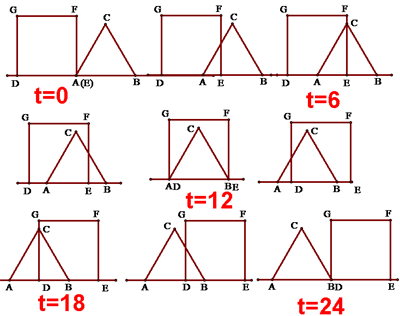
例12  如图，正三角形ABC和正方形DEFG的边长均为12，DE在直线AB上，△ABC固定不动，正方形DEFG向右移动。从A,E重合到B,D重合为止，每秒运动1，运动时间为t，重叠部分面积为s，求s与t的函数解析式。

细心的人是怎样解题的呢？他会将整个运动过程全部画出来，包括特殊的和一般的情形。图形如下：

能这样细心细致地考虑问题的人，今后还不是成大器的人吗？

十一、知难而退

在解数学题时常常一条自己认为可行的思路，其实是一条死路或艰难之路，懂得知难而退的人或许能更快成功。

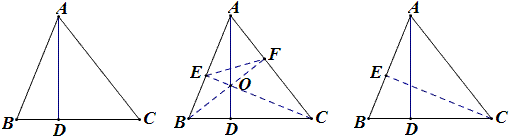
例13  如图，△ABC中，∠BAC=60°，AD是高，BD=1，CD=2，求△ABC的面积。

思路1：

设AD=x，得到tan\angle{BAD}=\frac{1}{x}，tan\angle{CAD}=\frac{2}{x}，

∴tan^{-1}(\frac{1}{x})+tan^{-1}(\frac{2}{x})=60，想解出x，这在初中阶段是死路一条。

思路2：

作高CE、BF，由∠BAC=60°，得

\frac{AF}{AB}=\frac{AE}{AC}=\frac{EF}{BC}=\frac{EO}{BO}=\frac{FO}{CO}=\frac{1}{2}，

然后设EO=a，FO=b，利用以上关系及众多的相似三角形列出方程，求出面积。

这个方法计算量很大，一般的人吃不消，知难而退吧。

思路3：

作高CE，设AD=x，得到AB=\sqrt{x^2+1}，AC=\sqrt{x^2+4}，

由面积法知\frac{1}{2}BC\times{AD}=\frac{1}{2}AB\times{CE}，又CE=\frac{\sqrt{3}}{2}AC

即\frac{1}{2}\times{3}\times{x}=\frac{1}{2}\times{\sqrt{x^2+1}}\times{\frac{\sqrt{3}}{2}\times{\sqrt{x^2+4}}}，

这个方程虽然是4次的，但没有奇次项，可以解出x^2=\frac{7+\sqrt{33}}{2}，（为什么舍去x^2=\frac{7-\sqrt{33}}{2}？请读者思考。）

进而解出x=\frac{\sqrt{11}+\sqrt{3}}{2}，

∴S_{\triangle{ABC}}=\frac{3}{4}(\sqrt{11}+\sqrt{3}).

十二、预见未来

现在的学生做事也好，解题也好都缺少这种能力，“写着再说”、“不知道做这一步为了什么”是目前学生的普遍现象。说不定从解数学题可以锻炼这种能力。

例14  已知实数a,b,c满足abc=1，求\frac{1}{ab+b+1}+\frac{1}{bc+c+1}+\frac{1}{ca+a+1}的值。

分析：如果先通分，预见一下，是相当麻烦的事。

如果运用条件abc=1，则可将第一的分式化为\frac{1}{\frac{1}{c}+b+1}，预见一下，下一步该做什么？分子分母同乘以c，这样可以与第二个分式同分母。再预见一下，第三个分母咋办？也可以化为同分母？对！只要先化为第一个的分母，再化为第二个的分母。

答案是1，解答略。

本题还可以将计算的代数式改为：求\frac{b}{ab+b+1}+\frac{c}{bc+c+1}+\frac{a}{ca+a+1}的值。其结果与原来一致。

十三、避难就易

我的经验告诉我，难的事情最后做，也许会收到意想不到的效果。

例15
如图，把正方形分成四块全等的直角三角形，再拼成四边形（非正方形），下列语句正确的是（　　）
A、能拼出6种不同的平行四边形 B、菱形是拼不成的 C、可以拼出2种不同的矩形 D、只能拼出1种等腰梯形
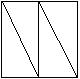如果先考虑A，就要拼出6种不同的平行四边形，这太多了，不容易。还是先考虑B,C,D吧，因为个数不多，容易啊，结果发现菱形有1个，矩形只有1个，等腰梯形有2个，所以A正确。

A难，B.C.D容易，这就是避难就易。

例16 求y=\frac{x^2-2x+1}{x^2-1}\div\frac{x^2-x}{x+1}-\frac{1}{x}+1的值时，下列语句正确的是（ ）
A、x=100和x=99的值是一样的 B、x=0和x=2的值是一样的
C、x=1和x=2的值是一样的 D、x= -1和x=2的值是一样的

分析：100和99太大了，先考虑简单的吧，因为x=0,2,1，-1时原式无意义，所以只能选择A了。

十四、旁门左道

例16  已知a是非零实数，则下列不等式一定成立的有（     ）

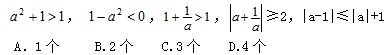分析：第4个不等式的判断有点困难，一般的初中生证不了，既然常规的方法难住自己了，那就来点旁门左道。

取a=1,-1,2,-2代入不等式成立，所以这个不等式应该是对的，还有对的是第1个和最后1个，故选C。

本题采用的方法成“特殊值法”。

结束语

我的课堂教学中，经常会遇到解题与做人不矛盾的例子，我会即时教育学生，虽然我知道我的很多学生未必能懂得其中的道理。由于没有及时记下，当时一些非常实际、非常贴切的例子遗忘了，以后继续收集中……