有时候解决问题的反面远比解决问题的正面来得简单。这是一种思想还是一种方法?我也说不清,反正很有效。生活中也有这样的做法,我常常猜想,是不是许多数学方法来自于生活?是不是许多数学思想源自于生活?这是一节我非常得意的数学专题课,我讲的专题是《从反面考虑问题》,这是一个成功的案例。
那天,狂风大作。我走进教室,习惯地带上门,可总是关不住,扫帚顶、凳子靠都不管用,学生似乎在笑。
这时我问同学们:谁有办法使风不把门吹开?同学们的建议还挺多,有的说用桌子顶,结果一试不行,风实在太大了。有的说用再重一点的东西来顶,可是找不到重一点的东西。有的说锁住门就行了,但锁坏了。许多建议无一成功,学生哑了。
我启发说:看来我们从风的进口做文章不行了,那我们就从它的反面来考虑。学生不知反面指的是什么,我又说风的进口反面就是出口啊,风的出口是什么啊?学生大悟,齐声说:窗!对!我说,如果解决了这个问题的反面,风吹不出去了,结果会怎样呢?学生无语。那好,请同学们把所有的窗都关了。我的话音刚落,大家一下就关好了窗。
我说:现在我们再关上门,不顶任何东西,你们猜门还会被吹开吗?学生无语,但怀疑的眼神分明不相信会有效果。可是事实使他们非常惊讶!咦?门怎么不开了?是不是风停了?其实这是物理现象,原来叫对流,现在无法对流了。
我利用这个机会,用强调的语气说:同学们,有时候解决问题的反面远比解决问题的正面来得简单。下面我用这个思想来解决几个数学问题(我常常分不清思想和方法)。
例1 有30个贰分硬币和8个伍分硬币,那么在1分至100分的100种整数币值中不能支付的有 种。
我先让学生做,结果学生的答案五花八门,但都知道1分和3分不能支付。对有些学生说的某些不能支付的币值,我一一作了反驳。如11分,5+6=11,13分=6+7,21分=10+11等。
我启发道:支付的反面是什么?学生无语。我只好道明:支付的反面是剩下!1分、3分不能支付就等于说1分、3分不能剩下。现在知道还有什么币值不能支付了吗?
这次学生答对了:还有99分和97分不能支付。
除了这4种外还有吗?我再启发:50分以上的不必考虑了,如51分能不能支付?只要考虑49分能不能剩下。偶数一定可以支付也不用考虑了,我们就考虑30到50 之间的奇数就可以了(1到29前面已经讨论,都可以的)。个位是5的不用考虑,因为35=30+5,45=40+5。个位是7的也一样。那么只剩下31、33、41、43四种没讨论了。很快学生都有方法支付。
结果只有4种不能支付。
例2 28个人进行拳击对抗赛(每场输的人退出比赛),到最后决出冠军为止,一共需要进行几场比赛?
学生的方法绝大多数是:
先分成14对比赛,退出14人剩下14人,再7对比赛退出7人,剩下7人中组成3对退出3人,剩下4人中再退出2人,最后一次比赛退出1人,冠军产生了。共27场比赛。
我摇摇头说:这不是我们今天想用的方法。我提醒大家:今天我们的主题是考虑问题的反面。比赛获胜的反面是什么?答:被淘汰。又问:最后一个人当冠军,那要淘汰几人?答:27人。每淘汰1人就要比一场,那要比几场?学生齐答:27场。
我看见了学生闪亮的眼眸。
例3 3个人中选2个有3种选法,4个人中选3个有4种选法,……,10个人中选9个有几种选法?
学生不假思索地说:10种。
一个学生解释说:有规律的,3个人3种,4个人4种,那么10个人就是10种。
我提醒道:这仅仅是猜想!谁能说说理由?
许久,一个学生举手,他说:10个人选9个就相当于剩下1个,共有10种剩法。
我要大家为之鼓掌。说:这就是反面考虑问题,已经有人会使用它了。我相信下面的问题有更多的同学会想到这个方法。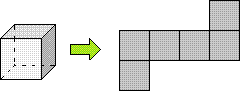
例4 如图,将一个正方体表面展开,至少要剪开几条棱?
我问一个学生:剪开的反面是什么?答:不剪开。我表扬了他。
我耐心等待,奇迹终于发生,陆续有人举手,最后有一半人做对了。一个学生说了他的想法:我考虑剪开的反面──不剪开,因为从图中看出有5条棱还连着,共有12条棱,所以有7条棱剪开了。
例5 若方程x^2+2x-2a+3=0和x^2+2x+a+5=0至少有一个方程有实数解,则实数a的取值范围是 ( )
(A)-4≤a≤1 (B) a≥-4 (C) a≤1 (D)a≤-4或a≥1
这道题选自数学竞赛,我是有意为难学生的,当然学生都不会。我不得不启发:不要忘了我们的思想。答:忘是没忘,就不知道找哪个问题的反面。再启发:找“至少有一个方程有实数解”啊,谁说说这个问题的反面?……
接下来发生的故事大家也能猜到,不累赘了。
的确,运用这种方法的机会不多,因为这样的题目不多。亲爱的读者,如果你有类似的题目,请在评论里给出,以丰富文章的内容。我这里先叩拜了。
老师就是老师,太厉害了