过去,我不会自己编题,备课、出卷都是东抄一题西抄一题的,时间花得多,三度难以达到,试卷质量差,效果不好。后来,我大着胆子自己尝试着编出几道题,很高兴、很管用。至今,编题数量已难以统计,所编的题在多种重大考试中使用,命题质量受到同行好评。
我越来越尝到了自己编题的甜头,备课轻松了,甚至不用备课。上课时的例题、练习题随手写来,随要随出。命题时基本上可以实现无纸化、无参考。自己觉得解放了、减负了,应付各类评比考试轻松了,提高了自己的业务水平。
那么,怎样才能编出好题呢?我想首先要做一个有心人,处处留心,处处关注。具体的说要做到以下几点:
- 加强对题目的记忆
- 关注各种题目之间的联系
- 解题留有余地(还有什么结论,条件如何改造,图形如何简化,与以前的题有什么联系等)
- 多思考,提高敏锐性
- 多观察,生活中有数学
- 关注学生的错误,它是编题的素材
- 错题可以收集,它是编题的素材
- 难题可以改编,它是编题的素材
- 有新的发现及时记录
- 个人奇特的见解是萌发编题的火花
- 以欣赏的目光看好题
下面介绍几种初中数学命题常用的编制方法。
1、学生的日常错误作为编题的素材
学生在作业、课堂练习、考试中经常会出现各种各样的错误,我们教师要关注、要收集。说不定就能因此编出好题来。
例1 如图所画的数轴正确的有( ) A、1条 B、2条 C、3条 D、4条
这是收集了学生画数轴时的错误所编的一道题,答案:A。
例2 有以下三个命题,判断这三个命题的正确性(在括号内打√或×)
①平行四边形是中心对称图形 ( )
②四边形中只有平行四边形才是中心对称图形( )
③平行四边形不是轴对称图形 ( )
在教一般平行四边形和特殊平行四边形关系时,学生表面上好像懂了,其实做了这一题后会发现,不懂的学生实在太多了,尤其是第②个,学生认为是错的,理由是还有矩形、菱形。答案:①√②√③×
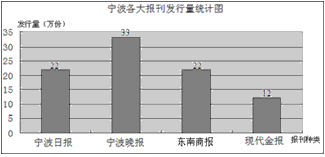
例3 如图,是根据媒体提供的消息绘制的“宁波各大报刊发行量统计图”,那么发行量的众数是( )
A、宁波晚报 B、宁波日报和东南商报 C、33万 D、22万
看似简单的问题,很多学生(包括一些老师)都选择了C,他们认为“33万”是最多的数据,这是对“众数”的曲解,也有选A或B的,怎么可以选报纸的名称呢?
有一次作业中做到这样一题:
长为30cm宽为10cm的正方形白纸按如下图所示的方法黏合起来,黏合部分的宽为3cm, (1)求5张白纸黏合后的长度,20张呢? (2)若x张白纸黏合后的长度为y(cm),写出y与x的函数解析式。
当时学生错误百出,课堂讲解后为了巩固我随手又编了一题:
例4 半径为1的圆形纸片按如下图所示的方法黏合起来, (1)求5张纸黏合后的长度,20张呢? (2)若x张纸黏合后的长度为y(cm),写出y与x的函数解析式。
结果很多人还是错,急中生智又编了下题:
例5 如上图,圆环的外径为8,内径为6,(1)6个这样的圆环套起来后拉紧的长度是多少? (2)若x个这样的圆环套起来后拉紧的长度为y(cm),写出y与x的函数解析式。
2、为了测试学生的某种能力而编题
为了测试学生的逆向思维能力,我编了下题:
例6 有30个贰分硬币和8个伍分硬币,那么在1分至100分的100种整数币值中不能支付的有 ( )
A.2种 B.4种 C.6种 D.8种
为了测试学生的运动能力,我编了下题:
例7 如图四边形ABCD中, AB=4,BC=7,CD=2,AD=x, 求x的取值范围。
例8 等腰梯形ABCD的周长为12,一个底角为60°,设较大的底边为x,那么x的取值范围是 。
为了测试学生的动手操作能力,我编了下题:
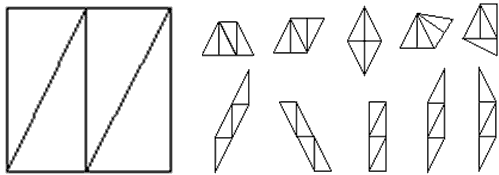
例9 大家都玩过七巧板吧,今天让你玩一玩四巧板。将一个正方形硬纸板按如图的方法分成一样的直角三角形,这样的四个三角形能拼成各种四边形,请问共有几种平行四边形?请你一一将图形画出来(正方形不算)
答案有10种,不动手操作怎能获得?
![]() 例10 如图一个长方形被分成6个正方形,有5格内写有字母A、B、C、D、E,另有一空格,每次可以将空格周围(上下或左右)的一个字母向空格作平移,要想将字母A平移至最右下角,至少要作几次平移?
例10 如图一个长方形被分成6个正方形,有5格内写有字母A、B、C、D、E,另有一空格,每次可以将空格周围(上下或左右)的一个字母向空格作平移,要想将字母A平移至最右下角,至少要作几次平移?
答案:11次
3、老问题编出新面孔
有一些很平常、很常见的题,你可不能习以为常、不以为然哦,或许可以改编成一道全新的题。但这需要你有敏锐的触角和洞察全局的思维。
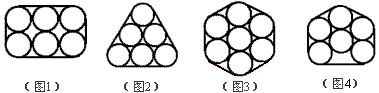
例11 有一道老题目:6罐可乐用图1、图2两种方式捆扎。(1)判别哪种捆扎一圈的绳子长?(2)在图1的基础上不解开绳子,再塞进一罐可乐,可行吗?
答案是可行的,如图3,因为一圈的绳子与图1、2一样长。我就萌发灵感,改编如下:
六听可乐罐有如图1、2、4三种捆扎方式,哪一种捆扎更牢固?为什么?
答案:图4捆扎更牢固,因为图4的一圈绳子长比图3更短。关于图4绳子长的计算,请参见《学生妙解数学题》的第6题。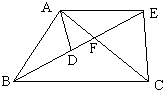
例12 常见的一道题:如图,D在直线BE上,BE交AC于F,△ABC∽△ADE,求证:△ABD∽△ACE。
挖掘出这道题的更多结论,编一道题:如图,D在直线BE上,BE交AC于F,△ABC∽△ADE,你还能找到更多的相似三角形吗?
答:还能找到2对: △AEF∽△BCF,△ABF∽△CEF。
例13 常见的一道题:如图,三角形ABC中,OB、OC分别平分∠ABC和∠ACB,设∠A=x度,∠O=y度。求y关于x的函数解析式并求x的取值范围。
挖掘出这道题的更多结论,编一道题:
1、∠O一定是什么角?为什么?
2、如图,以△ABC的边BC为弦,在点A的同侧画弧BC交AB于D(弧DC>弧DB), 在弧DC上取点P,连PB、PC,已知 ∠BPC=90^\circ+\frac{x}{2}. (1)当∠A=50°时,求∠BDC的度数;(2)判定△ADC的形状,并说明理由;(3)当PB平分∠ABC时,求证:PC平分∠ACB. (4)是否存在这样位置的P点和AB上一点M,使得△BMP和△BPC相似?若存在,请在备用图中画出所有符合条件的图形;若不存在,请说明理由.
解1:∵y=90^\circ+\frac{x}{2},∴90<y<180,∠O所以是钝角。
解2:这道题是典型的旧题变新题,是某年我区初三统考试题。是我和小梅合作的结晶。本题改编的思路是:
将已知(角平分线)和结论(y=90^\circ+\frac{x}{2})对换.第(4)题是受到下面这道题的启发: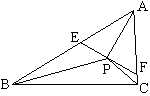
如图,△ABC的内角平分线交于P,过P作EF⊥PA,求证:△BEP∽△BPC。
4、观察生活引发编题灵感
生活中有数学,数学可以解决生活问题,很多生活实际问题从来没有人用数学眼光看待,一旦你扑捉到了,你就是第一人。下面几例是我的得意之作。
例14 电台里的播音员正在播《葫芦娃的故事》,“蝎子精举着大刀劈向三娃,三娃金刚铁臂,他手起刀落,啪!啪!啪!蝎子精的刀被劈成了3段,……”。这段故事中有个错误,请你改正 。
这是我儿子小时候听磁带听出来的问题:“爸爸,啪!啪!啪!三下应该的4段,这位叔叔讲错了”。
例15 电信部门推出付100元钱享受120元的通话费的业务,对用户来说优惠了( )
A、20% B、16.7% C、15% D、12%
这是我老婆告诉我广告消息后引发的故事,广告说:大优惠了!付100元钱享受120元的通话费,优惠20%。
例16 小明家的餐桌周围放有6把椅子,妈妈拖地有个习惯,先把椅子搬开,拖干净后再把椅子照原样放好,这样就算2次移动。那么要把餐桌周围的地拖干净,一共需移动 次椅子。 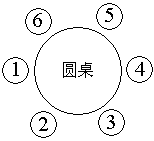
这是小时候我妈妈叫我干活干出来的。我为了偷懒就如图那样将1号椅先移到外面,拖好后,将2号椅放到1号椅的位置,拖好2号椅的位置,将3号椅放到2号椅的位置,以此类推,一共7次移动就行了。
例17 两人猜拳时各出一手,握拳表示0,伸一指表示1,依次类推.我们把两拳相加的数称为拳数。①问猜中拳数为5的概率是多少?②如果猜中拳数者为胜,那么猜拳的人为什么喜欢猜拳数为5?
这是年轻时候喝酒喝出来的题。过去不懂为什么猜5算输的道理,现在想想还真有道理,制定这个法则的人是数学家啊。
例18 某次数学考试,因试卷难度大而导致成绩普遍很差,老师为了提高学生的分数,采用将每人分数先开方再乘以10的方法。如36分的人计算方法是10\times\sqrt{36}=60,即经过这样处理后的分数比原来高了24分。一个爱动脑筋的同学发现:不同的成绩增加的分数不一样多。请问几分的人经过处理后加分最多?说明道理。
以前,由于没有控制好试卷难度,使得考试成绩普遍偏低,老师就用这种方法来调整分数,由于这个学生的好奇,使我获得了编题的素材。解此题可以设经过处理后的分数为x分,增加的分数为y分,那么y=x-\frac{1}{100}x^2,该函数的最大值是25.
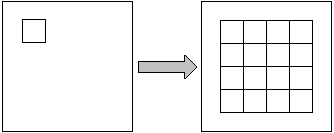
例19 有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形,粘贴的图形又可以进行任意的平移。我们把复制、粘贴各一次或不复制只粘贴一次叫做一次操作。如图,现已有一个正方形在窗口,至少要进行 次操作,才能在窗口中出现4×4的正方形网格。
这是玩电脑玩出来的题。
5、为了运用某种数学方法而编题
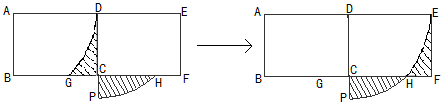
例20 如图,两个完全相同的长方形ABCD和CDEF拼在一起,已知AB=1,AD=a,以A为圆心,a为半径画弧,交BC于G;以D为圆心,a为半径画弧交DC延长线于P,交CF与H,当两个阴影部分面积相等时,则a的值是 (π取3).
这是考查学生平移变换运用能力。 从左边的原图平移到右边的图,使两个阴影部分放在同一个矩形中,就容易沟通数量关系了。
例21 甲打擂台,有乙、丙来应战,假设每人战胜对方的可能性一样大,则甲打擂成功的可能性是( ) A、1/2 B、1/3 C、1/4 D、1/6
这是考查学生运用乘法原理的能力,这道题用树形图或列表的方法学生相当困难,如果考虑甲要打擂成功必须分两步战胜乙和丙,胜的概率分布都是1/2,这样两个1/2相乘就得到1/4. 选C.
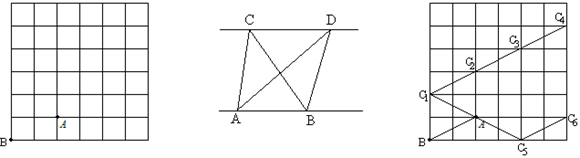
例22 如图6×6的正方形网格中,每个小正方形的边长为1,格点上已有2点A、B,再找一个格点C,使△ABC的面积等于2,这样的C点共有 点。
6、根据考试意图编题
例23 某地一辆汽车牌照为“ZS-659”,由于下雨,牌照在地面有倒影,那么开在该汽车前面的同向汽车里的司机从后视镜里看到它在地面倒影是 ( )
水倒影是上下轴对称的,照镜子是左右轴对称的,既有水倒影又有照镜子,即既有上下轴对称又有左右轴对称,也就成为中心对称了,这是生活常识。
例24 线段y=-\frac{1}{2}x+a(1≤x≤3),当a的值由-1增加到2时,该线段运动所经过的平面区域的面积为 ( )
A.6 B.8 C.9 D.10
考试的意图就是考一次函数,这样的题就编得有新意了,不过也难了。
例25 有如下一些正方体表面展开图,要考学生正方体表面展开图的概念。亲爱的读者,你会如何编题?
我是这样编的:
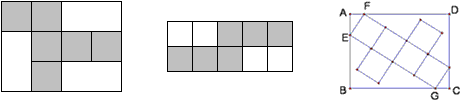
(1)如左图,在一个周长为14cm的长方形里,剪出一个正方体表面展开图,这个正方体的棱长是多少?
(2) 我们可以在面积为3×4的矩形中画出多种棱长为1的正方体的表面展开图. 请你设计一种面积比3×4更小的矩形,使得我们能在其中画出棱长为1的正方体的表面展开图,并画出这个正方体的表面展开图.(答案如中图)
(3) 如果给你同样的面积为3×4的矩形,请你在其中画出棱长大于1的正方体的表面展开图,并计算你所画正方体的表面展开图折成正方体后的棱长.
解:如右图设计,AB=3,BC=4,则△AEF∽△BGE,且相似比为1:4,设BE=x,那么AE=3-x,AF=x/4,BG=4AE=12-4x,CG=4-BG=4x-8,∴4x-8=x/4,∴x=\frac{32}{15},∴AE=\frac{13}{15},AF=\frac{8}{15},EF=\sqrt{(\frac{13}{15})^2+(\frac{8}{15})^2}=\frac{\sqrt{233}}{15}>1.
篇幅过长,以下内容转至下一页“初中数学题的编制方法(续)”。
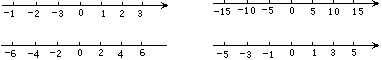




《初中数学题的编制方法》有一个想法