“实验”不是物理、化学的专利。用实验解决数学问题,是近几年来新理念下的热门题型。这样的问题往往不需要复杂的计算和推理,只需动手操作,实验观察即可。这是对学生动手能力、想像能力和观察能力的挑战。《数学课程标准》从“基本理念”到“总体目标”再到“课程实施建议”都提出了数学实验的要求,那么教师怎样在课堂教学中落实这个要求呢?我在这方面进行了较多的尝试,下面谈谈如何用实验解决某些初中数学问题。
数学实验方法1——正确作图,仔细度量
某些几何计算题(选择题或填空题,下同),直接解有一定困难,如果按题意准确作图(甚至要用圆规),再用刻度尺或量角器或圆规进行度量比较,得到结果。
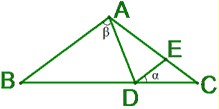
例1、如图,△ABC中,AB=AC,D在BC上,E在AC上,AD=AE,设∠EDC=α,∠BAD=β,那么α与β关系正确的是 ( )
A、β=α B、β=2α C、β=2.5α D、β=3α
实验:画图时应讲究技巧,先画∠BAD=60°,再任画射线BD,然后用圆规截取AC=AB,AE=AD,那么便可量出∠EDC=30°,故选B。
我曾在一个有48位学生的班级作了统计,经常用这个方法的只有2人,偶尔用这个方法的有15人,其余从来没有用过这个方法。
事后,我找了一个从来没有用过这个方法的学生谈话。
师:你为何不用这个方法?
生:因为这个方法不严格,我们的老师不让用,所以我不敢用。
数学实验方法2——借助工具,巧思妙想
有些数学问题可以借助一些器物来进行实验,如下面两例中的铅笔和绳子。
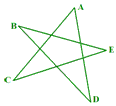
例2、如图,求∠ A+∠B+∠C+∠D+∠E的度数。
实验:用一支铅笔,按下图的方法进行转动,每次都用顺时针的方向,转过内角的度数。
请看,转过5个角后铅笔的方向反了,转了180°,即为5个内角的和。这个方法适用于求各种多边形(包括凹多边形)的内角和。
例3、一个等腰三角形的周长为12厘米,那么这个等腰三角形的腰长x的取值范围是 。
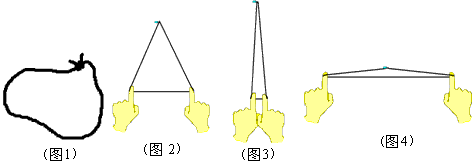
实验:取一条绳子,打一个结做成一个圈(如图1),将圈挂在墙上的一枚钉子,用两个手指将圈绷紧,做成一个等腰三角形(如图2)。然后将手指靠拢,做成图3的等腰三角形,这时腰长比较接近于6。再将手指拉开,做成图4的等腰三角形,这时腰长比较接近于3。故3<x<6。
数学实验方法3——用计算器,探求规律
例4、20世纪最伟大的数学家诺伯特·维纳,他在很年轻时就获得哈佛大学博士学位。在授予学位那天,有人打听年轻博士的年龄,维纳十分有趣的回答:“我今年岁数的立方是一个四位数,岁数的四次方是一个六位数,把这个四位数和六位数各位上的数字从小到大排列在一起,恰好是0,1,2,3,4,5,6,7,8,9这十个数字,一个不重,一个不漏,这就意味着全体数字向我靠拢,向我祝贺,预祝我将来成为一个伟大的数学家。”这位博士的年龄是 岁。
实验:计算器是探索本问题规律的最好工具。先从立方是一个四位数、四次方是一个六位数入手,锁定年龄在18至21岁之间。18的三次方是5832,18的四次方是104976,所以维纳的岁数为18岁。
数学实验方法4——利用电脑,幻想成真
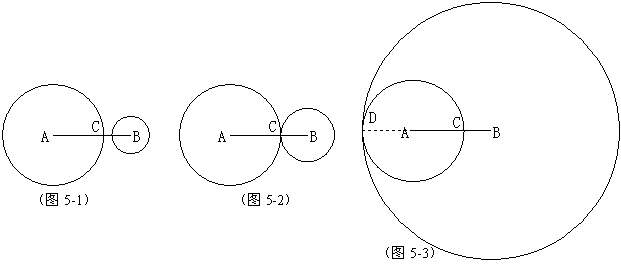
例5、⊙A和⊙B相交,⊙A的半径为5,AB=8,那么⊙B的半径r的取值范围是 。
实验:用“几何画板”软件,先画线段AB=8,再画⊙A的半径为5,然后画⊙B半径为变量(如图5-1),变化⊙B半径,使⊙B与⊙A外切(如图5-2),这时r=3。再变化⊙B半径,使⊙B与⊙A内切(如图5-3),这时r=13。故3<r<13。
虽然我们不要求学生会使用“几何画板”软件,考试中使用电脑的可能性也不大,但是我们的着眼点不应该光盯着考试。我的学生几乎每人会用“几何画板”软件,他们的数学实验就比别人多了一种方法。当然本问题还可以通过画图和想象来达到目的,不过下面的例6想象是有困难的,而电脑可以使你幻想成真。
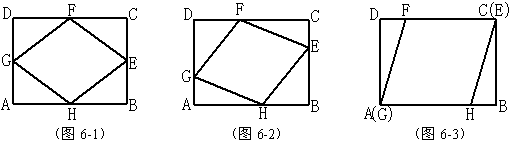
例6、如图6-1,矩形ABCD中,E、F、G、H在四条边上,使四边形EFGH为菱形,问菱形EFGH有几种不同的位置?
实验:用“几何画板”软件画出矩形ABCD,在AB、AD上任意取两点H、G,作菱形EFGH,则拖动H和G可以得到无数个菱形EFGH,其中图6-1为各边中点的情形,是所有菱形中面积最小的。图6-2是一般情形。图6-3是G与A重合的情形,是所有菱形中面积最大的。
答:菱形EFGH有无数种不同的位置。
你一定看到电脑在数学实验中的重要性了吧!
数学实验方法5——模拟实验,形象直观
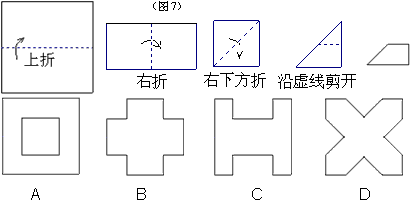
例7、如图7,把一个正方形纸片三次对折后沿虚线剪下,则剩下的部分展开后的图形是( )
解决这类问题,只要进行模拟实验即可,问题要我们怎样做,我们照办行事就是了。要注意的是不要折错了方向。
与例1一样,为了说明动手操作的重要性,我在这个班级上课时,先不让学生动手,而是通过想象得出结论。结果48人中25人选A,3人选B,15人选C,5人选D。待学生通过实际操作得出正确结论是B时,大家才发现想象与实际情形的距离太大了。但还是有8人,他们操作的结果不是B,这说明实验也得仔细。
例8、如图8,一个长方形被分成6个正方形,在5格内写有字母A、B、C、D、E,另有一空格。每次可以将空格周围(上下或左右)的一个字母向空格作平移。要想将字母A平移至最右下角,至少要作几次平移?
实验:也采用模拟实验。剪5张正方形纸片,写上A、B、C、D、E,按图8放在桌面上,再按问题要求进行移动,多次实验后发现移动9次最少了。
数学实验方法6——画图操作,体会细节
有些数学问题(包括几何、函数等),只要画出大概的图形,就可以分析得出解决问题的方法。这里的画图与方法1中的作图有很大区别,作图力求准确,而画图只需大概的草图就行了。
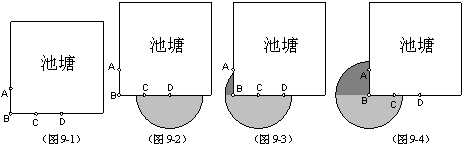
例9、如图9-1,边长为12 m的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3 m.现用长4 m的绳子将一头羊拴在其中的一棵数上,为了使羊在草地上活动区域的面积最大,应将绳子拴在( )
A、A处 B、B处 C、C处 D、D处
实验:分别以D、C、B为圆心,4为半径在池塘外画圆弧,弧与池塘边所围成的区域如图9-2、图9-3、图9-4所示(以A为圆心的区域与以C为圆心的区域一样大),很明显答案应该是B。
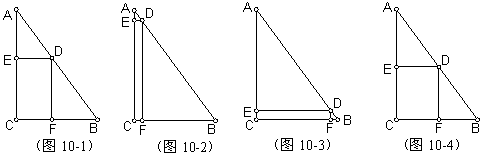
例10、如图10-1,Rt△ABC中,AC=8,BC=6,D是斜边AB上的一个动点(不与A、B两点重合),DE⊥AC于E,DF⊥BC于F,D从靠近A的某一点向B移动,矩形DECF的周长变化情况是( )
A、先大后小 B、先小后大 C、逐渐增大 D、逐渐减小
实验:先画出D很靠近A的图形(如图10-2),这时矩形DECF的周长接近16。再画出D很靠近A 的图形(如图10-3),这时矩形DECF的周长接近12,至此只能排除答案C。再让D移动至AB中点,这时矩形DECF的周长为14,所以我们有理由猜想答案是D。
用实验解决数学问题,关键是有没有进行实验的想法和敢不敢试一试的胆量。伟大的科学发现无不进行大量次实验才成功的,愿我们的学生在实践中大胆去想,放手去做,经常品尝实验带给我们的丰硕之果。
[slideshare id=3146964&doc=random-100212003851-phpapp02]
后记
这是一节由公开课教案改编的文章。当时听课的有数学课标编写组专家和由张奠宙教授带领的中学数学骨干教师高级研修班成员。课后,有三位听课者评课。
评课者1对这节课给予高度评价,并给予“武林高手”的美誉。
评课者2对这节课不屑一顾,并给予“投机取巧”的评价。
评课者3是张奠宙教授,他说:如果把整个数学教学比作一道菜,那么这节课只能作为佐料,而我们平时的常规课堂教学是主料,佐料太多或太少都会影响一道菜的味道。
对于评课者1,我要说的是谢谢,因为他是我多年交往的知音。
对于评课者2,我认为评价相当确切。有机会来了,不抓住机会怎么行?可以用实验解决的问题并不是太多,出现了就要抓住机会,这就是“投机”。解决数学问题关键在于一个“巧”字,多少人为了这个“巧”而煞费苦心,所以要“取巧”。
张教授的评价是非常中肯的。确实,实验解决问题的方法不是解题方法的主流。它仅仅是一种点缀,是“佐料”,甚至是让一些学生应付考试、多得一点分数的没有办法的办法。


《怎样用实验解决初中数学问题》有2个想法