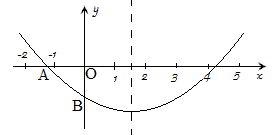讨论数学教学经验和辅助软件使用
关于x的二次函数y=ax^2+bx+c图象如图所示。
（1）判断c-4b的符号；（2）判断a-2b+4c的符号；（3）如果OA=OB，求证：0<a<1.
解（1）
由\frac{b}{-2a}>1，得b<-2a，即-2b>4a，
∴c-4b=-2b-2b+c>4a-2b+c=f(-2)>0.
（2）
a-2b+4c=4(\frac{1}{4}a-\frac{1}{2}b+c)=4f(-\frac{1}{2})<0.
（3）
∵OA=OB，B点坐标为（0，c），∴A点坐标为（c，0），
∴ac^2+bc+c=0，ac+b+1=0，
∵f(1)<0，即a+b+c<0，∴b<-a-c，
∴ac-a-c+1>0，即(a-1)(c-1)>0，
∵c-1<0，∴a-1<0，即0<a<1.
今天上课的内容是复习二次函数，我随手编了一道题，学生只会做第（1）题，现拿出来与大家共享，并考考你。如果你在下面评论里写出了正确的解答，将会获得一套初三培优试卷作为你的奖励。
关于x的二次函数y=ax^2+bx+c图象如图所示。
（1）判断c-4b的符号；（2）判断a-2b+4c的符号；（3）如果OA=OB，求证：0<a<1.
在上一篇文章《请你来画图！》中，提出了几个有关平行线的画图问题，其中最后一个图使许多人发生了困惑，究其原因，是思维定势在作祟。当AB∥CD时，C、D的顺序可以交换。其实在很多时候我们的思维都会有定势，如画一个三角形就想不到是钝角三角形；画一条高，就一定在形内；想到同侧就想不到异侧；想到点在线段上就想不到点在线段外……
现在就《请你来画图！》中的问题，我给出所有情形的解法。
已知两条线段AB∥CD，点E不在AB、CD所在的直线上。∠ABE=α，∠CDE=β，∠BED=γ。请你就E点的不同位置尽可能多的画出各种图形，写出该图形中α、β、γ的关系，现在解法1已经给出，其余解法只给出α、β、γ的关系，请你在方框内画出每种解法相应的图形。
解法1：如果所画的图形是如图所示的图形的话，那么有γ=α+β
解法2：如果所画的图形是如图所示的图形的话，那么有α+β+γ=360°
解法3：如果所画的图形是如图所示的图形的话，那么有β=α+γ（要画出2种不同的图形）
解法4：如果所画的图形是如图所示的图形的话，那么有α+β+γ=180°(α、β、γ都≠90°)
挑战你的想象能力和创新能力，期待你的参与。由于评论中不能附图，所以建议你做个图片的超链接。
一道考学生的几何变换───平移的题，受到大家的热情参与，首先谢谢参与者。
开始自己编的题，自己也解错了，我原先的答案是5次粘贴（见左图）。后来，一位小学五年级的学生（秦维杰）告诉我，只需4次粘贴就可以了（见右图）。
好一个5年级的小学生，对图形的感觉真好！
在操作画图板时，我发现要画出如下的图形方法很多，但最快的方法是先画一个最小的三角形作为基本图形，然后通过变换的方法进行复制、粘贴，拼合而成。
请你回答：至少粘贴几次，才能拼成这样的图形？（不考虑复制、变换的次数）
你的答案直接在评论里给出。我会公布我的答案。
关于画图板的介绍，请参见《数学画图的好帮手──画图板》一文。
没想到才过4天，一道几何作图题征集到多人的解答，并在QQ群（出众树雪88730268）上引起大讨论，看来数学研究就得这样，有问题大家研究，有结果大家分享。
一位老师问我：在一个长8厘米、宽6厘米的长方形内画两个圆，这两个圆的面积之和最大是多少？
因为百思不得其解，于是想用几何画板绘制图形，以探索最大值的位置。但作图遇到了困难，也就是
在几何画板中想作如下的图形，结果发生了困难，请教高手解答。
给定矩形ABCD，先作一个最大的圆P，要在余下的矩形区域内再作一个最大的圆Q。
可是圆Q的圆心如何确定呢？我百思不得其解。也就是在已经画出矩形ABCD和圆P后怎样用尺规作出圆Q，请大家支招！
我分析来分析去，最终将问题转化为如下的作图题。
已知∠ABC=45°，定点P在角内部，请在射线BC上找一点Q，使得Q到AB的距离等于PQ。
以上问题等待你的解答，求助了。
为了提高本博客的互动性，我在上篇文章《征求解答》中提出了一个初中数学问题：
如果\alpha为锐角，那么sin{\alpha}+cos{\alpha}的最大值为\sqrt{2}。
请你将证明过程在下面评论里给出，证明的依据不能超过初中知识。
本问题的结论是我很早时候自己发现的，我想一定会引起更多老师的兴趣。结果征集到五位老师的四种解答（有些解答在QQ中交流），公布如下。