有人说数学是思维的体操。的确,数学是一门非常能锻炼人脑的课程,通过初中数学的学习,我觉得它使我掌握了一种分析问题的方法,使我受益匪浅。
数学分析方法指的是,利用长期学习数学中培养的解题途径,然后通过逻辑思维推理,得出相应的结论。数学的分析方法分为“综合法”与“分析法”两种。
所谓综合法,是指在解题过程中,从已知出发,根据一些性质和定理,一步一步地推理得出新的结论,最后得出问题的结论。俗称“顺向思维”。让我们举例说明。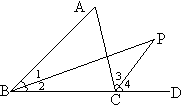
例1 如图\triangle{ABC}中,\angle{ABC}的角平分线与\angle{ACB}邻补角的平分线交于P,\angle{A}=x^\circ,\angle{P}=y^\circ,试用x的一次式表示y。
分析说明:
根据题目,从条件“\angle{A}=x^\circ”推出\angle{ABC}+\angle{ACB}=180^\circ-x^\circ或\angle{ABC}+x^\circ=\angle{ACD}。
由另一个条件“\angle{ABC}的角平分线与\angle{ACB}邻补角的平分线交于P”推出\angle1=\angle2=\frac{1}{2}\angle{ABC},\angle3=\angle4=\frac{1}{2}\angle{ACD}。
由此可以得到,\frac{1}{2}\angle{ACD}-\frac{1}{2}\angle{ABC}=\angle4-\angle2=\angle{P}。而开始得出的结论有x= \angle{ACD}-\angle{ABC}。这两个结论就有了联系,从而推出\angle{P}=\frac{1}{2}(\angle{ACD}-\angle{ABC})=\frac{1}{2}x。
所谓分析法,就是在解题过程中,从结论出发,把结论步步倒退,根据逻辑思维的规律性,考虑由什么条件可得出这个结论,直至与已知条件接轨。俗称“逆向思维”。也举例如下。
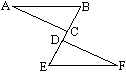 例2 如图,已知AB//EF,AB=EF,BD=CE,说明\angle{A}=\angle{F}。
例2 如图,已知AB//EF,AB=EF,BD=CE,说明\angle{A}=\angle{F}。
分析说明:
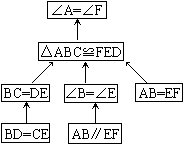
根据题目,从问题出发,要说明\angle{A}=\angle{F},就要说明\triangle{ABC}\cong\triangle{FED},要说明\triangle{ABC}\cong\triangle{FED},就要证明三个要素①AB=FE,②BC=ED,③\angle{B}=\angle{E}。其中第①已知,第②就要根据BD=EC说明。
∵BD=EC,∴BD-CD=EC-DC(即BC=ED),第③就要根据AB//EF说明,∴\angle{B}=\angle{E}。通过这样分析再解题,就轻而易举了。
在这两种方法基础上,又产生了第三种方法,就是两种方法的结合。我们看下面的例子。
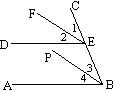
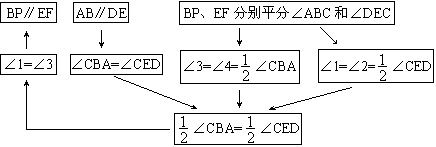
例3 如图,AB//DE,BP、EF分别平分\angle{ABC}和\angle{DEC}。求证:BP//EF。
分析方法:
先用分析法。从问题出发,要推出BP//EF,就要推出\angle{1}=\angle{3}。
再用综合法。从已知出发,条件“AB//DE”可推出\angle{CBA}=\angle{CED},条件“BP、EF分别平分\angle{ABC}和\angle{DEC}”可推出\angle{3}=\angle{4}=\frac{1}{2}\angle{ABC}及\angle{1}=\angle{2}=\frac{1}{2}\angle{DEC}。和分析法联系起来就有\angle{1}=\angle{3},这样就可以证明了。
数学的分析方法有且只有这样3种,不同的题目采用不同的分析方法,其中采用较多的是第三种方法。善于分析的同学,分析问题时常有一条思路,虽然这条思路不见得马上将已知和结论联系起来,但多训练以后,路子越来越宽、越来越多、越来越顺。不善于分析的同学,解题的思路形不成一条线索,只有“蜻蜓点水”,永远提不高分析能力。分析方法是从我们的实践中找到的、积累的。所以,每个同学都可以自己去创造、发现,大胆地去探索,说不定某一天你就成为一个大数学家。
点评:这个学生能关注人的分析过程,这是一个很高的境界!还能将分析过程图示化,更是难能可贵。这篇小论文在我们学校1999年首届学生小论文评比中荣获一等奖。
《数学的分析方法──2001届陈海波(初二)》有一个想法