几何画板真是好东西,画图时无意间发现了如下两个命题。
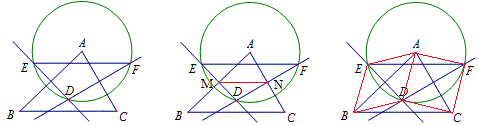
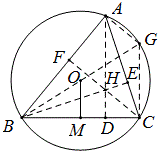
一、如图,作△ABC两边AB、AC的中垂线交于D,⊙A经过D,且与两条中垂线交于E、F,求证:EF=BC。
解法1:
如图,连MN,由垂径定理可知AM垂直平分ED,AN垂直平分DF,那么MN既是△ABC的中位线,又是△DEF的中位线,
故EF=BC。
解法2:
如图,由AB、DE互相垂直平分得四边形AEBD是菱形,同理四边形AFCD也是菱形,所以BE和CF平行且星等,
故四边形BCFE是平行四边形,那么EF=BC。
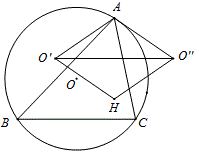
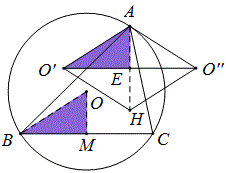
二、已知△ABC内接于圆O,H是垂心,O关于AB,AC的对称点为O’,O”,求证:四边形AO’HO”为菱形。
本题中的O,O’,O”,分别是上题中的D,E,F,所以易证AO’=AO”,O’O”与BC平行且相等,因为H为垂心(即△ABC高的交点),所以直线AH是O’O”的中垂线,所以HO’=HO”,其余的解法如下。
解法1:
以O’为圆心、O’A为半径作圆,在弧AB上任取一点E,连EA,EB,AH,BH,BO’,由垂心性质可知∠AHB=180°-∠C,
∠AO’B=∠AOB=2∠C,所以∠E=∠C,所以∠E和∠AHB互补,所以H在圆O’上,故O’A=O’H,所以四边形AO’HO”是菱形。
解法2:
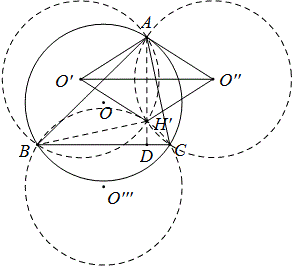
以O’,O’’为圆心,OA为半径作圆交于H’,那么AH’⊥O’O”(连心线垂直平分公共弦),
因为O’O”∥BC,所以AH’⊥BC,AD是高。
同理以O”’为圆心,OA为半径作圆也交于H’,且BH’也是高,
那么H’即为垂心H,所以AO’HO”是菱形。
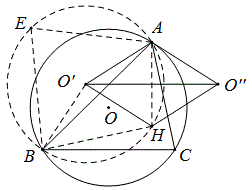
解法3:作弦心距OM,因为AO’=OB,AE、OM以及BM、O’E均平行,故△AO’E≌△OBM,所以OM=AE。
又因为AH=2OM(三角形一个顶点到垂心的距离等于外心到对边距离的2倍),所以E是AH的中点,
所以AH与O’O”互相垂直平分,即四边形AO’HO”是菱形。
解法3中命题“三角形一个顶点到垂心的距离等于外心到对边距离的2倍”的证明。
已知:O为△ABC的外心,H为垂心,OM是弦心距。
求证:AH=2OM。
证明:如图添出辅助线,易证AG∥CF,CG∥AD,所以四边形AHCG是平行四边形,所以AH=CG=2OM。
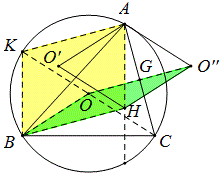
解法4:
设圆O的半径为R,
如图作辅助线,易证四边形AKBH为平行四边形(理由同上)。
所以BH=AK=2OG=OO”,所以BH∥OO”,所以OBHO”是平行四边形,所以O”H=OB=R=AO”,
即四边形AO’HO”是菱形。
还发现,
(1)当∠BAC=45°时,菱形变成正方形。
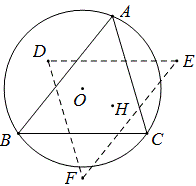
如图画O的三个对称点D,E,F,那么还有这样的一些结论:
(2)三角形DEF与三角形ABC全等;
(3)O是三角形DEF的垂心,H是三角形DEF的外心