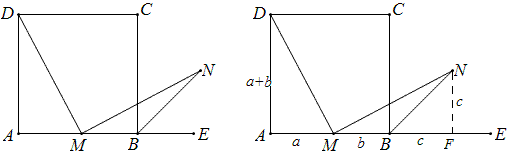前面已经有很多学生妙解的例子了(共32题),具体的见:
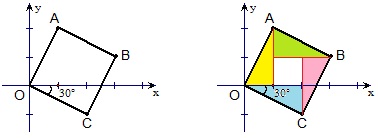
例33 下图中,正方形的边长是4,写出A、B、C的坐标。
如图作弦图,则B到y轴的距离是2\sqrt{3}+2,B到x轴的距离是2\sqrt{3}-2,
故B点的坐标是(2\sqrt{3}+2,2\sqrt{3}-2)。
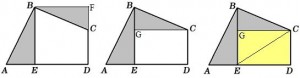
例34 已知Rt△ABC中,∠ACB=90°,AC=6,BC=8。
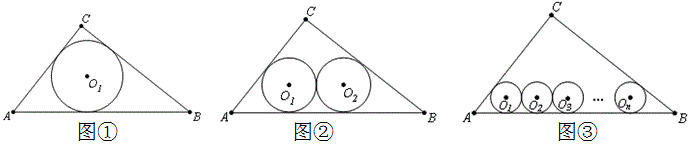
(Ⅰ)如图①,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
(Ⅱ)如图②,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2;
(Ⅲ)如图③,当n大于2的正整数时,若半径rn的n个等圆⊙O1、⊙O2、…、⊙On
依次外切,且⊙O1与AC、BC相切,⊙On与BC、AB相切,⊙O1、⊙O2、⊙O3、…、⊙On-1均与AB边相切,求rn.
2012届初三周洁的解答:
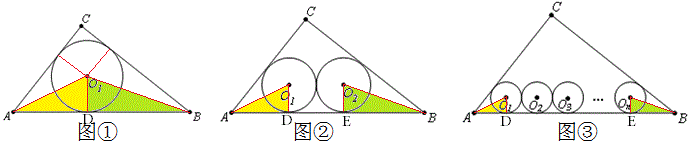
如图,在图1中可以算出O1D=2,AD=4,DB=6,所以\frac{O_1D}{AD}=\frac{1}{2},\frac{O_1D}{DB}=\frac{1}{3},于是可以在图2、图3中可以证明所有黄色的三角形相似,所有绿色的三角形相似,那么设O_1D=r,在图1中就有AD=2r,DE=2r,EB=3r. 2r+2r+3r=10,r=\frac{10}{7}。
同理,在如3中AD=2r,DE=2(n-1)r,EB=3r. 2r+2(n-1)r+3r=10,r=\frac{10}{2n+3}。
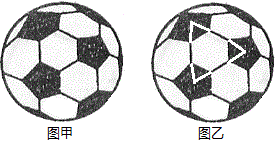
例35 有一种足球是由32块黑白相间的牛皮缝制而成的(如图甲),黑皮可看做正五边形,白皮可看做正六边形,求出白皮、黑皮各多少块?
小学2012届六年级袁祎铭解答:
如图乙,将每一个六边形与3个\frac{1}{5}的五边形组合在一起,这就说明1个六边形对应着\frac{3}{5}个五边形,故六边形的个数与五边形的个数之比是5:3,所以白皮块数=32÷(3+5)×5=20,黑皮块数=32÷(3+5)×3=12.
例36 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x1,0),且1<x1<2,与y轴的正半轴的交点在点(0,2)的下方,则下列结论①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1>0中正确的是____________。(写出序号)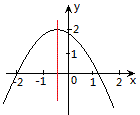
1012届初三洪骋娴解答:
①显然a<0,b<0,由图可知对称轴在-\frac{1}{2}的右边,故-\frac{b}{2a}>-\frac{1}{2},解之a<b;
②将(-2,0)代入解析式得4a-2b+c=0,4a+c=2b>2a,故2a+c>0;
③将(-2,0)代入解析式得4a-2b+c=0,4a+c=2b<0;
④将(-2,0)代入解析式得4a-2b+c=0,2a-b=-\frac{1}{2}c,
∵0<c<2,∴2a-b=-\frac{1}{2}c>-1,即2a-b+1>0.
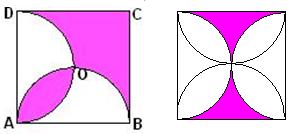
例37 如图,正方形ABCD的边长为8cm,分别以AB、AD为直径画半圆,求图中两个紫色部分面积的差的绝对值。
老师的解法:
设小的紫色部分为S1,大的紫色部分为S2.
设想将两张半圆纸片放于桌上,这是白色部分一层纸,S1有2层纸,S2有0层纸。再揭掉正方形部分纸片,这样白色部分0层纸,S1有1层纸,S2有-1层纸,即为S1-S2.
∴│S1-S2│=│2S半圆-S正方形│=64-16π.
2013届初二毛向宇解答:
两个紫色部分面积的差的绝对值,即为第二个图中的紫色部分面积。
例38 如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE等于_____。
常规的解法:
如图1,旋转△ABE至△BCF,将四边形ABCD转化为正方形BEDF.
13届初二8班周喆旻的解法:
如图2,作CG⊥BE于G,可得两个灰色的三角形全等,设AE=BG=y,BE=CG=ED=x,则x(x-y)+xy=8,解得x=2\sqrt{2}.
2013届初二史梦倩解答:
如图3,作CG⊥BE于G,连EC,则两个灰色的三角形全等,两个黄色的三角形全等,
于是△BEC的面积为四边形ABCD面积的一半,即BE×CG÷2=8÷2,BE2=8,x=2\sqrt{2}.
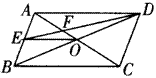
例39 如图,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点 F, 若S□ABCD=24,则S△DOE的值为多少。
老师解法:∵四边形ABCD是平行四边形,∴O是BD的中点,
又∵E为AB的中点,∴OE∥AD,∴S△DEO=S△AEO=\frac{1}{8}S□ABCD=3.
2013届初二8班孙一如解答:
∵四边形ABCD是平行四边形,∴O是BD的中点,
又∵E为AB的中点,∴S△DEB=\frac{1}{2}S△ABD,
S△DOB=\frac{1}{2}S△DEB,∴S△DB=\frac{1}{4}S△ABD=3.
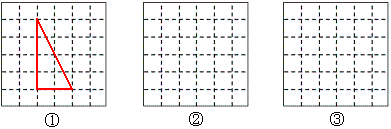
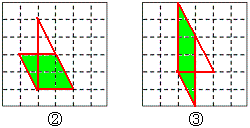
例40 如图所示,在6×6 的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图①中的三角形是格点三角形.
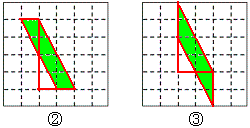
请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两种格点平行四边形(非矩形),画在图②,图③,中。
老师的解法:
2013届初二8班周喆旻提出歧义:
这不符合“画一条直线将格点三角形分割成两部分,将这两部分重新拼成两种格点平行四边形”,这两种拼法分割线不一样了,应该是同一条分割线,拼成两种不同的平行四边形。
2013届初二张朝欣解答:
例41 如图,正方形ABCD中,M是AB上一点,E是AB延长线上一点,MN⊥DM交∠CBE的角平分线于N,求证:MD=MN.
老师的方法:
在AD上取一点G使AG=AM,再证△DGM≌△MBN。
2013届8班陶心的解法:
如图作NF⊥AB于F,设AM=a,BM=b,BF=NF=c,
由△DAM∽△MFN,得\frac{a+b}{b+c}=\frac{a}{c}
可求出a=c,∴△DAM≌△MFN,故MD=MN.
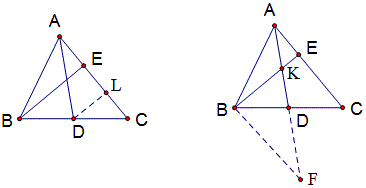
例42 如图△ABC中,点D、E分别在BC、AC上,BE⊥AC,BD=DC,∠DAC=30°,求证:AD=BE。
老师的证法:
作EC的中点L,连结DL,由Rt△中30°的性质知AD=2DL,又由中位线性质知BE=2DL,故AD=BE.
2013届初三沈超群的解法:
延长AD至F,使DF=AD,由∠DAC=∠F=30°及BE⊥AC、BF⊥BE知AK=2KE,KF=2BK,故AF=2BE,又AF=2AD,所以AD=BE。
例43 若二次函数y = ax2 + bx + c(a ≠0)的图象过点(0,1)和(–1,0)且顶点在第一象限,则S = a + b + c的值的变化范围是 ( )
A、0<S <1 B、0 <S <2 C、1 <S <2 D、–1< S< 2
2013届初三郑晨扬的解法:
S = a + b + c是x=1时函数的值,从下图可以看出,S的值介于0与2之间,所以选B.