前面已经有很多学生妙解的例子了(共23题),具体的见:
自从我留心学生巧妙的解法,财富有了明显的积累,累累硕果被永久保存。当我向同行展示这些妙解时,无不为之震撼—-学生太聪明了,老师弯腰了。
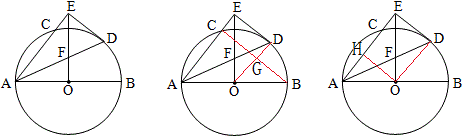
例24 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.⑴求证:DE是⊙O的切线;⑵若\frac{AC}{AB}=\frac{3}{5},求\frac{AF}{DF}的值。
对于第(2)题有2个同学提供了自己的解法。
2011届初三6班桑晨的解法:
如图,连BC和OD,设AC=3,AB=5,则易证四边形ECGD是矩形,易算GD=1,故AE=4,由△AEF∽△DOF得\frac{AF}{DF}=\frac{AE}{OD}=\frac{4}{2.5}=\frac{8}{5}.
2011届初三蒋晨微的解法:
如图,连OD,作弦心距OH,先证明EH=OD,算出AE=4,其余与上法相同.
例25 已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线O-A-B-D的路线移动,移动的时间为t秒.设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围.
学生有4种不同的方法.
方法1:作PQ⊥AB于Q.
S=S_{OABC}-S_{\triangle{OCD}}-S_{\triangle{BPQ}}-S_{PQAO}.
方法2:过P、D作y轴的垂线段,垂足为E、F,
S=S_{\triangle{OPC}}-S_{\triangle{ODC}}.
方法3:作OH⊥CB,垂足为H,
S=\frac{1}{2}PD\times{OH}.
方法4(由1011届刘泽汉提供):由方法3可知,S是t的一次函数,设为y=kx+b,
当P与B重合时,容易算出此时t=18,S=8,当P与D重合时,容易算出此时t=23,S=0,将这两对对应值代入后,用待定系数法即可。
例26 如图O是正三角形ABC内任意一点,过O点作三边的垂线,垂足分别为D、E、F,求证:S_{\triangle{AOD}}+S_{\triangle{BOE}}+S_{\triangle{COF}}=\frac{1}{2}S_{\triangle{ABC}}。
2011届初三李嘉毅解法:
如图,过O点作三边的平行线,则图中出现6对面积相等的三角形,故原来黄色三角形面积=白色三角形面积。
例27 如图O是等腰梯形ABCD的上底AD上一点,OE垂直BC,求证:阴影部分的面积是梯形面积的一半。
2011届初三李嘉毅解法:
如图,补上两个直角三角形,得到一个矩形,设其面积为S。
则有m+n+b=\frac{1}{2}S,即m+n=\frac{1}{2}(S-2b),
也即,阴影部分的面积是梯形面积的一半。
例28 如图矩形OABC,O为坐标原点,A在x轴上,C的y轴上,B点坐标为(9,6),D在BC上,沿OD将△OCD折叠,C落在E。根据下列条件求出D点的坐标。
(1)E在AC上;(2)E在直线y=2x-6上。
(1)由C,E关于OD对称,得OD⊥AC,∴△OCD∽△CBA,∴CD=6÷9×6=4,∴D(4,6).
(2)易知F(0,-6),G(6,6),故OC=OF=OE,∠OEF=∠OFE,
∵∠OEF+∠DEG=90°,∠OFE+∠DGE=90°,∴∠DEG=∠DGE,∴DE=DG=DC,∴CD=3,∴D(3,6).
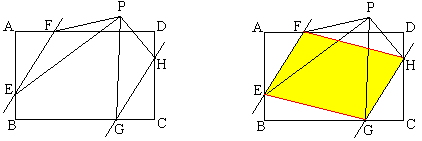
例29 如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别边上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,则△PEF和△PGH的面积和等于 。
2011届2班黄沁雨的解答:
用矩形面积减去四个直角三角形的面积,算出黄色部分的平行四边形面积为11,而△PEF和△PGH的面积和等于平行四边形的一半,所以答案是5.5
例30 (重庆2010年)含有同种果蔬但浓度不同的A、B两种饮料,A种饮料重40千克,B种饮料重60千克现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同,那么从每种饮料中倒出的相同的重量是______千克。
2011届2班王宁静的解答:
设倒出的质量为xkg,则得\dfrac{x}{60-x}=\dfrac{40-x}{x},
解得:x=24.
(在这里,\dfrac{x}{60-x}和\dfrac{40-x}{x}都表示A饮料和B饮料的质量比,如不管原来A饮料和B饮料的浓度如何,A饮料取1kg、B饮料取2kg混合与A饮料取3kg、B饮料取6kg混合所得的饮料浓度相同)
例31 某商厦进货员预测一种应季衬衫能畅销,就购进了8万元这种衬衫,面市后果然供不应求。于是商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批的2倍,但每件单价贵了4元。商厦销售这种衬衫的单价为58元,最后剩下150件按8折销售,很快售完。商厦第二批进的衬衫多少件?
1308班(初一)姜楠忆的解法:
假如第一批买了16万元,则数量和第二批相等,这样一共贵了17.6-2×8=1.6万元,因为每件贵了4元,所以第二批的件数是1.6÷4=0.4万件。
说明:这题多数人是用分式方程解的,该生用这么简单的算式就搞定了,不可小视啊。
例32 为加快西部大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程。如果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则刚好如期完成。问原来规定修好这条公路需多长时间?
1308班(初一)陶心的解法:
“现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则刚好如期完成。”
这句话说明:乙做规定时间+甲做4月=1
“乙工程队单独施工就要超过6个月才能完成”
这句话说明:乙做规定时间+乙做6月=1
这说明:甲做4月=乙做6月,所以做同样的工作量,甲时间:乙时间=4:6=2:3
又因为:乙做规定时间+乙做6月=1=甲做规定时间
所以做同样的工作量甲乙时间相差6月,故单位时间=6÷(3-2)=6(月)
规定时间=甲做的时间=6×2=12(月)
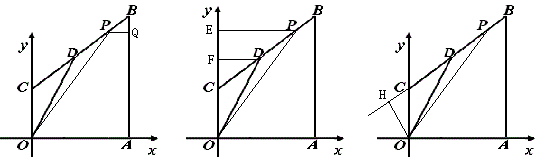
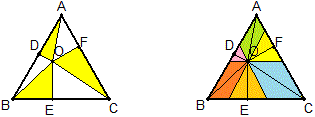
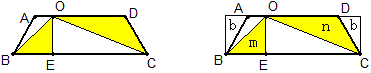
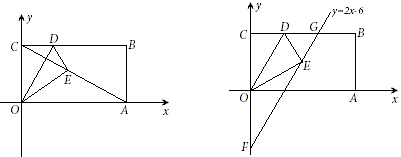
现在学生真的越来越聪明了,呵呵。希望您以后多多上传精彩题目的学生巧解。