极端原理在解题中的应用

在代数和几何里常有求一个变量的取值范围，通常都用不等式解之。我发现好多时候可以用极端原理来解，所谓极端原理就是取一个变量变化范围的两个极端，一个是极大端，一个是极小端，从而解决问题的方法。下面举例说明。

例1  一次函数y=2x-3，已知x的取值范围是-2<x<2，求y的取值范围。

分析：x的取值有两个极端，大的极端是2，小的极端是-2，将它们分别代入解析式得到y的两个极端1和-7，所以-7<y<1。

而一般的解法是先变形成x=\frac{y+3}{2}，再列不等式-2<\frac{y+3}{2}<2，这样计算量就大了。

例2  已知抛物线y=ax^2-2ax-1+a(a>0)与直线x＝2，直线x＝3，直线y＝1，直线y＝2围成的正方形有公共点，则a的取值范围是______．（注：直线y＝1即为过（0,1）点平行于x轴的直线）．

分析：画出草图如图。当a>0时，抛物线过C点是最低位置（其中的一个极端），此时C(3,1)代入得，9a-6a-1+a=1，a=\frac{1}{2}.  抛物线过A点是最高位置（其中的另一个极端），此时A(2,2)代入得，4a-4a-1+a=2，a=3.  抛物线位置上的两个极端必定是a的值的两个极端，故a的取值范围是\frac{1}{2}\le{a}\le{3}.   当a<0时，无解.

另外，我们可以从解析式看出，不论a取什么非零实数，抛物线的对称轴总是直线x=1，总是过（1，-1）点，这点是抛物线的顶点。所以当a变化时，抛物线不会左右平移，也不会上下平移，而是在顶点不变的情况下，改变开口的大小和方向。可见这个图形画得不对，但a的变化会使抛物线过两个极端是对的。

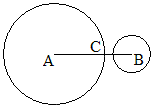例3  ⊙A和⊙B相交，⊙A的半径为5，AB=8，那么⊙B的半径r的取值范围是          。

分析：一般的解法是，解不等式│5-r│<8<5+r，这个很麻烦，况且还带着绝对值。我的方法是，先考虑r的极小端，此时两圆外切（如图1），r=3；再考虑r的极大端，此时两圆内切（如图2），r=13. 故3<r<13。

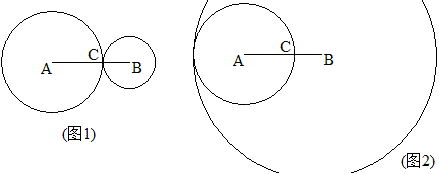
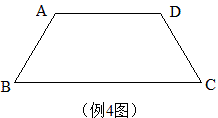例4  如图等腰梯形ABCD的周长为24cm，∠B=∠C=60°，设AB=xcm，等腰梯形ABCD的面积为ycm。求y关于x的函数解析式及自变量x的取值范围。

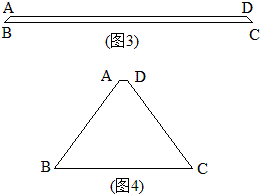分析：我们就求x的取值范围加以分析。常规方法就不说了，我的方法是用“极端原理”。AB的极小情况是图3，这时x可以很接近于0，AB的极大情况是图4，这时梯形接近于等边三角形了，x接近周长的\frac{1}{3}了，即x接近于8.

所以x的取值范围是0<x<8.

我们还可以从这两个图中知道BC的取值范围是8<BC<12.

例5  如图四边形ABCD中，AB=4，BC=7，CD=2，AD=x，求x的取值范围。

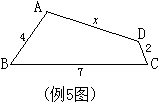分析：极端原理就是考虑x最大大到什么程度，最小小到什么程度，图5和图6就是这两个极端，极大端是x=13（当然我们这里说的极大端是指x可以无限接近13），极小端是x=1（当然我们这里说的极小端是指x可以无限接近1）。于是，x的取值范围是1<x<13.

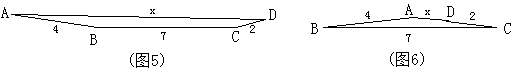
许多人解这道题时都连对角线，转化为三角形的三边关系，列出不等式组，结果很少有人成功。所以可以这样说，几何中的取值范围的问题绝大多数都可以用极端原理来解，千万不要先考虑不等式。

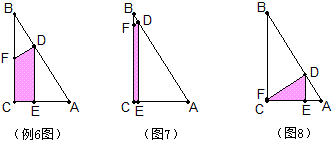
例6  如图Rt⊿ABC中，∠C=90°，AC=6，BC=8，点D在AB上，DE⊥AC交AC于E，DF⊥AB交BC于F，设AD=x，四边形CEDF的面积为y。求y关于x的函数解析式及自变量x的取值范围。

分析：我们就求x的取值范围加以分析。用极端原理先画出两个极端情况的图形，图7是x的极大端，此时x无限接近10，图8是极小端，此时x无限接近3.6，所以3.6<x<10.

看了以上解法，你基本了解了极端原理是如何在求变量的取值范围中运用的，无非就是抓住两个极端，画出两个极端情况的图形，求出两个极端时候变量的值。怎么样？是不是比列不等式容易多了？

如果你认为极端原理只能用在求变量的取值范围的话，那你就错了。下面这道题就是例证。

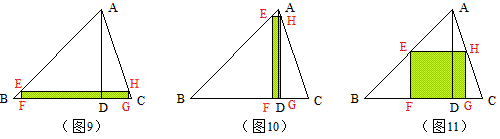
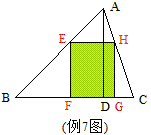例7  如图，△ABC中，BC=8，高AD=6，矩形EFGH的顶点在三角形的边上，则矩形EFGH的面积最大值是                     。

分析：考虑E点的两个极端位置，一个是靠近B点直至与B重合，此时矩形面积为0（如图9），另一个是靠近A点直至与A重合，此时矩形面积也为0（如图10）。可以预见到，这是一个二次函数的问题，两个极端正是二次函数图象的两个对称点。所以最大值就出现在这两个对称点的中间，也就是E在AB中点时达到最大值（如图11）。

最大面积=8÷2×6÷2=12.

我常对学生说：“几何里的取值范围问题，我们一般用极端原理来解”，我不敢将“一般”换成“一定”。今天终于找到了一题，发现很难用运极端原理，倒比较适合用运不等式。特追加下例：

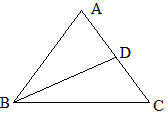例8  如图△ABC中，AB=AC，D在AC上，BD=AB，求∠A的取值范围。

解：设∠A=α，那么∠ADB=α，∠C=\frac{180-\alpha}{2}，因为∠ADB>∠C，∠A+∠ADB<180，所以

\left\{\begin{matrix} \alpha>\frac{180-\alpha}{2}\\2\alpha<180 \end{matrix}\right.，

得出60<\alpha<90，

这个结论是极端原理较难考虑的，因为极端位置不好寻找。