一段数学探究活动纪实

今天给学生讲解一道很平常的几何题：

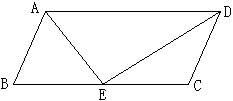
如图，平行四边形ABCD中，AD=2AB，E是BC的中点，求证：∠AED=90°.

解完后，我对同学们说：

我经常告诫大家，解题后要留有思考余地，本题我们能思考什么呢？

大家讲了一些可以思考的问题，但没有讲到我希望的内容，我只好直截了当抛出了问题：

难道我们不可以想想，除了BC的中点可以使∠AED=90°，BC上就没有其它点也有这个结论了？

我于是画出如下图形。

其实抛出这个问题的时候，自己心里也没底。

这时，大家就活跃开了。有些说没有了，有些说应该还有一点，还有些说好像还有几点。

我也和学生一起思索着……，相似，圆，方程，勾股定理，这些念头一一闪过。

我知道，当四边形ABCD为矩形时，这样的点只有中点。但现在条件是平行四边形，难道也只有一点吗？

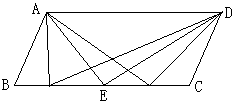
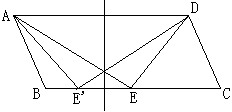
此时学生还没有结论。我突然想到了轴对称变换。

如图，将△AED沿着AD的中垂线反射得△AE’D，岂不是找到了第二个点了吗？

我将这个图形画出来后，学生都看明白了，似乎问题已经解决。但我意识到这个E’点有可能会跑到BC的延长线上，可是学生没有想到。于是，再问：

同学们，难道说任何情况下，BC上总有两个E点使∠AED=90°？

这一问，有学生反应过来了，有人说有可能E’点会在BC的延长线上。

我乘机再问：

那么BC上有2个还是1个这样的点，与平行四边形的什么有关？

这次大家都想到了，与∠B的大小有关！

我就顺水推舟：

大家继续探究，当∠B在什么取值范围时BC上有2个这样的点？

我发现学生似乎有点困难，就启发道：

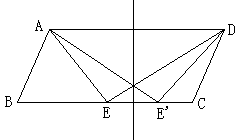
我们运用“极端原理”试一试，即当E与C重合时∠B是几度？

有学生很顺利地画出如下图形。

推导出此时∠B=60°.

一位学生说：我有答案了，∠B<60°

另一位反驳：错了，应该是∠B>60°

经过一段时间的酝酿，大家都同意后一位的观点。

我反问：当∠B=90°如何呢？

学生又有想法了，慢慢地大家将答案统一成60°<∠B<90°.

在这期间，我始终是一位参与者、合作者和引领者，自己也是在摸着石子过河，没想到一个不经意的问题引发了这么多的思考，挺有成就感的。但我的脑子里依然想象着∠B的动态过程，忽然一个念头出来了，∠B为钝角时也有2个点E位置的可能！

于是就追问：你们肯定60°<∠B<90°这个答案了吗？

学生当然说肯定。

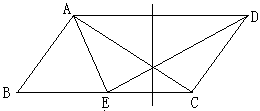
我只好提醒：当∠B为钝角时呢？

因为学生想象有困难，我画出了如下的图形：

又一次来到了高潮，有学生不以为然说：这只是前面情况反过来（反射），不需考虑了。

也有学生给出了更完整的答案：60°<∠B<120°且∠B≠90°.

似乎圆满了。忽然一位学生又发言了，60°和120°都能取到。是啊，怎么就没想到线段BC上的点可以取在端点上？这是许多学生的想法。

经过这么一番探究，最终获得了一个崭新的命题：

平行四边形ABCD中，AD=2AB，E是线段BC上的点，∠AED=90°，为使E有两个不同的位置，∠B的取值范围是60°≤∠B≤120°且∠B≠90°.

 

多么有意义的一节课，我和学生们一起经历了提出问题、探究问题和解决问题的过程，编出了一道前所未有的几何题，我的学生再一次尝到了数学探究的甜头，双赢啊。

这样的数学课我经历得不多，记得有过几次，还写了一篇博客，有兴趣可以看看《学生的能力不可低估》，我很珍惜这样的机会，恐会遗忘，故撰斯文。