职评中的说课

不论是中评还是高评，都有评说课的，分数占30%以上，但从我担任4次评委来看，大多数参评老师说课都打不到高分。究其原因，有以下几方面。

1. 没有按要求内容说课。现在职评说课一般都说一节课的片段，如只说新课引入，或者概念教学，或者例题教学等。不要去说教学目标、重点难点、教材地位、学生现状等。
2. 说课无新意。按书本顺序、书本情景、书本例题、书本解决问题的方法来说课，毫无新意可言。
3. 重点内容漏讲或不清。一些基本概念的教学，没有讲深讲透，有些模糊不清，甚至漏下没讲。
4. 说课中有错误。笔误、口误的发生，甚至是科学性的错误，会使说课的质量大打折扣。
5. 引入不得当。引入的情景有失偏颇，不能起到画龙点睛的作用。
6. 没有预见到学生的困惑。学生在什么样的内容上会发生困难，教师应在说课中加以点明。
7. 没有学生活动。学生是课堂教学的主题，所以学生的学习活动显得尤其重要，如果都是教师的讲解，没有学生的活动，学生只是一个听客，这样的课绝对不是好课，于是说课的质量也就不高了。
8. 回答评委的提问质量低下。说课20分钟里包含了5分钟的提问和回答。这个环节最能体现教师的基本功，许多老师因为平时缺少对教学的研究和思考，应对评委的提问慌不择手，答非所问。

成功的说课标准只有一个，那就是让人听得出，按你说课里说的方法去上课，一定是一节好课。下面以《锐角三角函数》为例，谈谈2009年江东区中级说课评比中出现的问题。

说课题目：请你说说初中数学九上《锐角三角函数》的概念教学，并说一说你是怎样突破教学难点的。

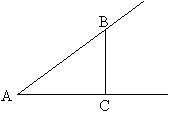
提问题目：书上“合作学习”1中：作一个30°的∠A（如图），在角的边上任意取一点B，作BC⊥AC于点C，计算\frac{BC}{AB}、\frac{AC}{AB}、\frac{BC}{AC}的值，并将所得的结果与你的同伴所得的结果作比较。有什么不利于教学的问题？

11个参评人员中有7人滔滔不绝地讲教学目标、重点难点、教法学法、教学理念。8人用斜坡、电梯作为引入，有些还问学生累不累的问题，这与三角函数没有多大关系。只有1人的讲法与函数有关，但还是没有讲清为什么角度与比值之间有函数关系，只有1人回答问题正确（这2人都得到高分）。只有4人让学生动手操作。有3人出现科学性错误，只有5人用相似三角形说明比值不变。还有一些小问题没有讲的人特别多，如“统称三角函数”、为什么是三个比而不是四个比、sin α不是sin与α相乘、∠的记号什么时候可以省略等等。

如果完全按教材的方法讲课，也是有问题的，因为教材也没有把函数关系讲清楚，教材中的节前语和引入都是不贴切的。但完全按教材顺序和内容说课的老师反而得分不低，这不能不说明这次参评的教师的基本功存在问题。

在面试回答问题时，评委希望参评老师能这样回答：因为Rt△ABC在书本上已经画出，学生都会度量书上图形的边长，所得数据是一个定值，这不利于说明比值\frac{BC}{AB}、\frac{AC}{AB}、\frac{BC}{AC}与边长的大小无关，只与∠A的大小有关。改进的方法是，在书本上只出现30°的∠A，不出现BC，让学生自行选取B点。

而我们的参评人员的回答，让人啼笑皆非。

• 老师1：30°量的话会近似，学生的答案会不相等。
• 老师2：三个比值一起出现学生会混淆。
• 老师3：30°太特殊，与函数没有类比。
• 老师4：学生会比较茫然，不知为什么求比值。
• 老师5：30°是一个定值，学生理解会偏差。
• 老师6：角的内部要作两条垂线。

这节课究竟怎样说课比较好呢？那就先解决怎样上好这节课的问题。下面就这节课谈谈我的设计思路，这样有助于说课的老师把握说课的内容。

• 思路1：先讲清sin α概念，cos α和tan α的概念顺水推出。
• 思路2：引入时不用斜坡或电梯的例子，就说：我们已经学习了几种函数，今天我们再来学习一种新的函数，这种函数的自变量是角度，应变量是两条线段的比值。顺便回顾函数的两个基本特点。
• 思路3：在黑板上画出三个角，度数分别是30°、45°、60°，分别构成直角三角形，求对边与斜边之比。可以发现，角度不一样，比值也不一样，同一个角，比值也唯一。
• 思路4：让每生在纸上画50°的∠A，再在以边上取点B，过点B向角的另一边作垂线，垂足为C，度量BC和AB，再算出\frac{BC}{AB}（精确到0.1）。问：大家的BC和AB值不一致，而比值为什么一样？利用相似三角形作解释。
• 思路5：由思路3和4可知，α与\frac{BC}{AB}存在函数关系，这种关系的表达式不好写，于是就用符号sin α来表示，即sin α=\frac{BC}{AB}，正像用根号表示平方根一样。
• 思路6：讲读法（有中文和英文之分），什么时候可以省略“∠”，什么时候不能省略，sin α不能理解成sin•α，正像\sqrt a不能理解成\sqrt{\quad}•a一样。
• 思路7：求sin30°、sin45°、sin60°、sin50°（用计算器）的值，说明sin60°≠sin30°+ sin30°，正像\sqrt{4+4}\neq2+2一样。
• 思路8：再讲余弦和正切的概念，方法与思路5一样，并说明还有3个比也有函数关系，这些初中以后学，讲正弦、余弦和正切统称三角函数，以及在直角三角形中的三角函数的关系。