解题的习惯有两种,一种是为了解题而解题,解完后不作任何思考,很快遗忘。另一种解题后有思考:本题的条件可以如何改造,结论可否拓展,图形可否改变,与以前的问题有何联系,解题方法带有哪些一般规律,等等。
两种不同的的习惯,反映了两种不同的价值取向。前者对数学不感兴趣,学习效率低下,后者对数学有强烈的好奇心,学习效益逐渐显露。我把解题后能进行思考的现象叫做“解题留余地”,留思考的空间,留拓展的余地。这个习惯很难养成,因为这需要很好的数学基础作支持。作为一名教师,这是专业能力和敬业精神的体现。
我坚持着“解题留余地”。逐渐地,想到问题深入了,得到结论深刻了,看到现象全面了,我能想到而别人想不到的时候多了。我经常思考些什么呢?下面以具体问题为例,来一一说明。
一、得出一般性结论
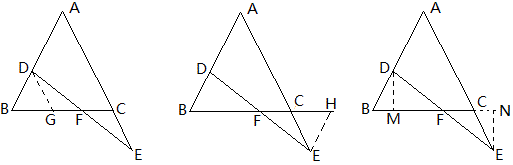
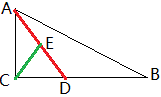
例1 如图,正三角形ABC中,D、E分别在BC、AC上,AE=CD=6,AD=9,求E到AD的距离。
分析:先证△ABD≌△BCE,后证△APE∽△BAE,还有∠APE=60°,再由AE^2=EP\times{EB}算出EP的长,即可知道EH的长。
思考:
1、从上题的图形中分离出一个基本图形(如下),图中的两个三角形△APE和△BAE,有公共角∠E和公共边AE,并且∠PAE=∠B,于是△APE∽△BAE,从而有结论AE^2=EP\times{EB}和\frac{AP}{AB}=\frac{AE}{BE}。这个图形我喜欢称为“两个公共”。
我们可以归纳出这样一个一般的结论:
如图,如果有两个公共的两个三角形相似,那么公共边是同一直线上的两边的比例中项,公共角所对的边之比等于相似比。(关于这个结论的应用,请见下一篇文章“几何中的基本模式”)
2、若正三角形ABC中,D、E分别在BC、AC上,AE=CD,则除了上面结论外,还有以下结论:
①有2对全等三角形;②有6对相似三角形;③∠APE=60°
二、归纳一般性方法
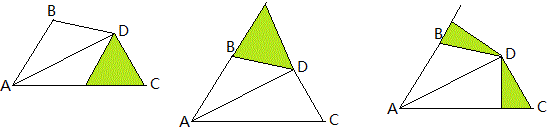
例2 如图,△ABC中,AB=AC,D在AB上,E在AC延长线上,BD=CE,DE交BC于F,求证:DF=EF。
分析:如下图1,作DG=DB,则可证△DFG≌△EFC。
思考:
△BDF和△EFC中,有BD=CE,∠DFB=∠CFE,DF=EF(虽然要证,但一定相等),可是这两个三角形却不全等。为什么有三对元素相等了,两个三角形还不全等呢?这是因为“边边角”的缘故。
我们发现,凡是“边边角”的两个三角形不全等的话,一定相差一个等腰三角形。所以本题的证明实际上是割掉一个等腰三角形。
也可以像图2那样补上一个等腰三角形,或者像图3那样割掉且补上半个等腰三角形(直角三角形)。
这样的解题方法再举一例。
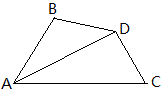
例3 如图四边形ABCD中,AD平分∠BAC,∠B+∠C=180°,求证:BD=CD。
和例2一样,两个三角形有三对元素相等,但却不全等,这是因为“边边角”的缘故。于是可以用割补法,添出如下图的辅助线。
三、问题深入和拓展
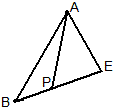
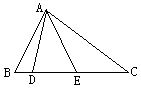
例4 如图△ABC中,D、E在BC上,AB=BE,CD=CA,当∠BAC=90°时,求∠DAE的度数。
这是一道极为普通的题目,计算结果为∠DAE=45°.我们可以思考些什么呢?
(1)结果的45°是条件90°的一半。难道当∠BAC=x°时,∠DAE=\frac{1}{2}x?
其实这个猜想是错误的,正确的结果是∠DAE=90-\frac{1}{2}x。
(2)当∠BAC变化时,∠DAE的有没有最大值?是多少?
当∠DAE=∠BAC时,∠DAE取得最大值,这时x=90-\frac{1}{2}x,x=60°.
(3)当∠BAC变化时,∠DAE的变化范围是什么呢?
答:0°<x≤60°.
前面我写过《一段数学探究活动纪实》也属于这个内容。
例5 如图,有不同形状的五个三角形,都已知了两个角的度数。请你分别在每个三角形中画一条分割线,将每个三角形分割成两个等腰三角形,并标出等腰三角形两个底角的度数。
解:分割线见下图。
解题后思考如下:
思考1:直角三角形一定可以分成两个等腰三角形吗(如1,2两个图)?答:可以,斜边上中线就是分割线。
思考2:一个角是另一个角2倍的三角形(简称“2倍角三角形”)一定可以分成两个等腰三角形吗(如3,4两个图)?
答:一般可以,但像二个角是50°和100°的三角形不能分。
思考3:2倍角三角形满足什么条件时一定可以分成两个等腰三角形?
答:设两个角分别为x和2x,则有x<180-x-2x,得x<45.
思考4:不满足x<45的两倍角三角形一定不能分成两个等腰三角形吗?
答:不是,如x=45时可以分。
思考5:如果两倍角三角形满足x>45,一定不能分成两个等腰三角形吗?
答:当三个角分别为x,2x,\dfrac{1}{2}x时,可以分的。这时可以算出x=\dfrac{360}{7}>45。
思考6:3倍角三角形一定可以分成两个等腰三角形吗(如图5)?
答:一定可以。
思考7:分成2个等腰三角形思考的差不多了,分成3个等腰三角形又如何呢?先考虑直角三角形吧。
思考8:锐角三角形是否一定可以将它分成三个等腰三角形?
答:可以,沿着三角形两边中垂线的交点和顶点的连线剪开即可。
思考9:钝角三角形一定可以分成三个等腰三角形吗?
正在茫然中……
四、变化图形的形状
例6 正方形ABCD中,CF平分外角,E在BC上,EF⊥AE交CF于F,求证:AE=EF。
证明时过E作等腰直角三角形BEG,可证△AGE≌△ECF。
思考1:正方形变成正三角形如何呢?
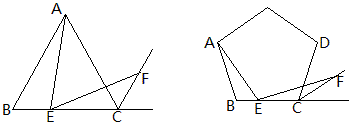
答:正三角形ABC中,CF平分外角,E在BC上,∠AEF=60°交CF于F,求证:AE=EF。
思考2:正方形变成正五边形如何呢?
答:正五边形中,CF平分外角,E在BC上,∠AEF=108°交CF于F,求证:AE=EF。
思考3:正方形变成其它正多边形如何呢?
答:……
五、与其它题的联系
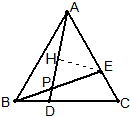
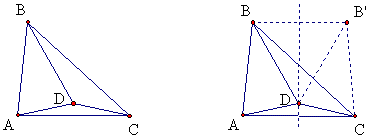
例7 如图,△ABC中,∠BAC=2∠BCA,D在三角形内,DA=DC,BD=BA,求证:∠ABC=3∠DBC。
证明:
如图,作B的对称点B’,则BC平分∠B’CA,
∵BB’∥AC,∴∠B’BC=∠BCA=∠BCB’,
∴BB’=B’C=AB=BD,故△BB’D为正三角形。
设∠BCA=∠B’BC=α,则∠DBC=60-α,∠ABC=180-3α,
故∠ABC=3∠DBC。
思考:
1、本题是下面这道题的拓展
已知△ABC是等腰直角三角形,∠BAC=90°,D在三角形内,DA=DC,BD=BA,求∠DBC的度数。
解题方法是补全一个正方形。
2、本题还有一个结论:∠BCD=30°。
3、点D不一定在三角形内,也可以在AC的下方,结论依然成立。
六、问题的反思与联想
例8 求x^2+\frac{1}{x^2}的最小值。
分析:我们将原式变形得:
x^2+\frac{1}{x^2}=(x+\frac{1}{x})^2-2,或x^2+\frac{1}{x^2}=(x-\frac{1}{x})^2+2.
那到底最小值是2还是-2?很多学生说取更小的一个-2.
反思1、x^2+\frac{1}{x^2}是一个非负数,不可能等于-2!
反思2、(x+\frac{1}{x})^2-2要取得最小值,必须x+\frac{1}{x}=0,这是不可能的,所以最小值不会等于-2.
反思3、既然x^2+\frac{1}{x^2}的最小值是2,那么由于x^2+\frac{1}{x^2}=(x+\frac{1}{x})^2-2,那么(x+\frac{1}{x})^2的最小值是4.
反思4、│x+\frac{1}{x}│的最小值是2.
七、其它的突发奇想
例9 已知a∥b,b∥c,求证:a∥c
上述结论和“若a=b,b=c,则a=c”有点类似,这种现象称为“传递性”,在数学中,传递性的关系还有哪些呢?
有传递性的关系用符号可以表示的有“∥”,“=”,“>”,“<”,“≥”,“≤”,“≌”,“∽”,
没有传递性的关系有“⊥”,“≠”,“倒数”,……
例10 如图已知AB∥DE,AC∥DF,求证:∠A=∠D。
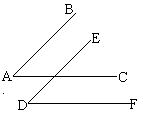
余地1:“如果两个角有两边分别平行,那么这两个角相等”是个假命题。
余地2:如果两个角有两边分别平行,那么这两个角相等或互补。
余地3:若角的两边都同向(或反向)平行,这两个角就相等;若角的两边一对同向一对反向平行,这两个角就互补。
余地4:如果同向平行记作“+”,反向平行记作“-”,相等记作“+”,互补记作“-”,那么本命题满足“符号法则”,即“正正得正,负负得正,正负得负,负正得负”。
余地5:数学中还有什么现象符合符号法则呢?
答:在繁分数中分母的分母是分子;平行为正,垂直为负,则负负得正;
余地6:在实际问题中,有什么现象符合符号法则呢?
答:敌人的敌人是朋友;反面的反面是正面。
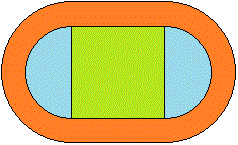
例11 体育场的跑道400米(内圈),跑道由2条直道和2条半圆形弯道组成,当直道长为─────米时,中间矩形场地(绿色)的面积最大。
分析:
设直道长为xm,矩形场地(绿色)的面积为ycm2,则
y=\frac{-2x^2+400}{\pi}.
当x=100时,y取得最大值。
思考:哦!原来100米直道不仅仅是比赛的需要,还能使矩形场地的面积最大。这个结论是偶然的?还是古人早就知道?否则为什么直道都是100米呢?
例12 下列图形中不可以折成正方体的是( )
这是一道在平常不过的题了,我想到了很多有意义的问题。
思考1:正方体表面展开图一共有几种?答11种。
思考2:这11种正方体表面展开图,是否都可以放入3×4的正方形网格中?答:有唯一的一个图放不下3×4的正方形网格中。
思考3:如图,我们可以在面积为3×4的矩形中画出多种棱长为1的正方体的表面展开图。我们还可以设计一种面积比3×4更小的矩形,使得我们能在其中画出棱长也为1的正方体的表面展开图。
这个设计图就是如下的图形。
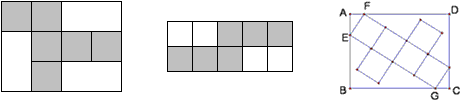
思考4:在同样的面积为3×4的矩形中,我可否在其中画出棱长大于1的正方体的表面展开图?
答:经过试验画出如下的图形:
通过计算得出正方形的边长是\dfrac{\sqrt{233}}{15}>1.
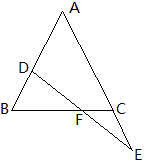






《解题留余地───浅谈数学题的拓展与思考》有一个想法