上接“初中数学题的编制方法”
7、根据解题方法编题
想知道自己讲过的解题方法学生掌握了没有,可以编几道题考考。
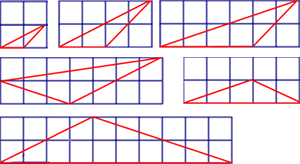
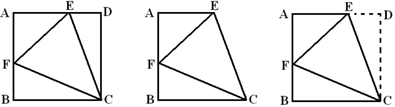
如学习平行线时,我们多次接触到如下图形。
把它们串到一起编一道题,效果不错。
例26 已知两条线段AB∥CD,点E不在AB、CD所在的直线上。∠ABE=α,∠CDE=β,∠BED=γ。请你就E点的不同位置尽可能多的画出各种图形,写出该图形中α、β、γ的关系,现在解法1已经给出,其余解法只给出α、β、γ的关系,请你在方框内画出每种解法相应的图形。
解法1:如果所画的图形是如图所示的图形的话,那么有γ=α+β
解法2:如果所画的图形是如图所示的图形的话,那么有α+β+γ=360°
解法3:如果所画的图形是如图所示的图形的话,那么有β=α+γ
解法4:如果所画的图形是如图所示的图形的话,那么有α+β+γ=180°
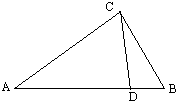 学习了相似三角形后,我们比较重视有“两个公共”的两个相似三角形,即如图D在△ABC的边AB上,且∠ACD=∠B,那么△ACD∽△ABC。这两个三角形有公共边AC和公共角∠A,所以称为“两个公共”的相似模式,它还有进一步的结论:AC^2=AB\times{AD}(公共边的平方等于同一直线上两边的积),CD:BD=相似比(公共角所对的两边之比等于相似比)。学生对这个方法掌握如何?编题如下:
学习了相似三角形后,我们比较重视有“两个公共”的两个相似三角形,即如图D在△ABC的边AB上,且∠ACD=∠B,那么△ACD∽△ABC。这两个三角形有公共边AC和公共角∠A,所以称为“两个公共”的相似模式,它还有进一步的结论:AC^2=AB\times{AD}(公共边的平方等于同一直线上两边的积),CD:BD=相似比(公共角所对的两边之比等于相似比)。学生对这个方法掌握如何?编题如下: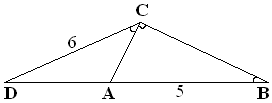
例27 △ABC中∠ACB=90°,AB=5,D是BA延长线上一点,∠DCA=∠B,DC=6,则tan∠DCA的值等于( )
A、\frac{3}{4} B、\frac{2}{3} C、\frac{3}{5} D、\frac{4}{5}
8、为了打破学生定势编题
学生解题往往会受到习惯定势所影响,这里的“习惯定势”指的是受解过的题影响,思维习惯等,也就是禁锢的思维,不够开放、不够发散。
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,D在AB上,作DE⊥AC于E,DF⊥BC于F,当D从A点向B点移动的过程中矩形DECF的最大值是多少?
本题中矩形DECF的变化情况是:先增大后减小,为了打破学生定势,我编题如下:
例28 如图Rt△ABC中,∠C=90°,AC=8,BC=6,D在AB上,作DE⊥AC于E,DF⊥BC于F,当D从A点向B点移动的过程中,矩形DECF的周长变化情况是 ( )
A、逐渐变大 B、逐渐变小 C、先变大后变小 D、先变小后变大。
又有一题,学生都是按常规的方法解的,即先建立以O为原点的坐标系,求出第一象限内的解析式,再求出B的坐标。
如图,某公园要建造一个圆形喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8米,水流在各个方向上沿形状相同的抛物线路径落下(如图),水流最高点距离水面1.8米,距离柱子水平距离1米。如果不计其它因素,那么为了喷出的水都落在池内,水池的直径至少为 ( )A、 米 B、 米 C、4米 D、3.8米
为了改变学生这种解题习惯,我编题如下:
例29 小张和小李同做如下一道题:(题目如上)
小张说:“我先建立以O为原点的坐标系,求出第一象限内的解析式,再求出B的坐标。” 小李说:“我不需要建立坐标系,也不求解析式,但我可以看出答案是哪个。” 请你先按照小张的说法写出解题过程, 选出正确答案;再按照小李的说法写 出思考的过程。
9、对已有的题目进行改造
例30 原题:如图,4×5的正方形网格中有一个△ABC,请你在此网格中画出2个三角形与△ABC相似,且彼此都不全等,使它们的顶点都落在小正方形的顶点上。
新题:如图,由边长为1cm的20个小正方形组成的正方形网格中有一个△ABC,请你在此网格中画出四个三角形与△ABC相似,且彼此都不全等,使它们的顶点都落在小正方形的顶点上。
别小看4×5换成2×10只是数据的变化,带来的是方法的变化,必须要从计算入手:
| 原三角形的边长 | \sqrt{2} | 2 | \sqrt{10} |
|---|---|---|---|
| 缩小\sqrt{2} | 1 | \sqrt{2} | \sqrt{5} |
| 扩大\sqrt{2} | 2 | 2\sqrt{2} | 2\sqrt{5} |
| 扩大2 | 2\sqrt{2} | 4 | 2\sqrt{10} |
| 扩大\sqrt{5} | \sqrt{10} | 2\sqrt{5} | 5\sqrt{2} |
| 先缩小\sqrt{2},再扩大\sqrt{5} | \sqrt{5} | \sqrt{10} | 5 |
| 先缩小\sqrt{2},再扩大2\sqrt{5} | 2\sqrt{5} | 2\sqrt{10} | 10 |
计算后可以画出如下6种图形:
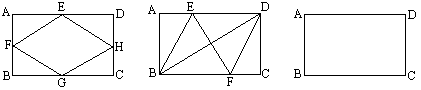
例31 原题1:如图,矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,求证:四边形EFGH是菱形。
原题2: 如图,矩形ABCD中,AB=4,BC=6,E、F分别是AD、BC上的点,四边形EBFD是菱形,求菱形的面积。
新题1:如图,矩形纸片ABCD中,AB=4,BC=6,从纸片上剪下一个菱形,使它的面积大于矩形的一半。
新题2: 如图,矩形ABCD中,AB=4,BC=6。(1)在图1中,E、F、G、H分别是AD、AB、BC、CD的中点,求菱形EFGH的面积;(2)在图2中画出一个比(1)中的菱形面积更大的菱形;(3)在图3中画出一个比(2)中的菱形面积更大的菱形,并计算所画菱形的面积。
解:(2)剪下一个正方形即可。(3)如原题2这样即可。
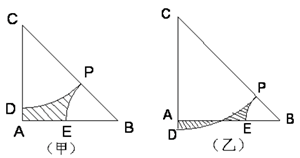
例32 原题: 如图甲,等腰直角三角形ABC中,AB=AC=\sqrt{2}cm,P在BC上,以C为圆心、PC为半径画弧交边AC于D,以B为圆心、PB为半径画弧交边AB于E,设PB=xcm,图中阴影部分的面积为ycm(π取3)。(1)求y关于x的函数解析式;(2)写出自变量x的取值范围;(3)当P在什么位置时,y有 最大值?最大值是多少?
新题: (4)如果我们取消D一定落在三角形边上的条件,也就是说D点可以落在CA的延长线上(如图乙),请问当x为何值时,两个阴影部分的面积相等?(保留两位小数)
例33 原题:将抛物线y=-2x^2+x-1向上平移几个单位,能使抛物线与坐标轴的三个交点构成直角三角形?
新题:将抛物线y=-2x^2-1向上平移几个单位,能使抛物线与坐标轴的三个交点构成直角三角形?
说明:原题的解答要用到抛物线与x轴交点的距离公式AB=\frac{\sqrt{\Delta}}{|a|},已经超出了目前的要求,而新题避免了这个问题。我们设抛物线y=-2x^2-1向上平移后为y=-2x^2+c,与y轴交于(0,c),与x轴交于(c,0),代入得0=-2c^2+c,解得c=\frac{1}{2},常数项由-1变到\frac{1}{2}向上平移了\frac{3}{2}个单位。
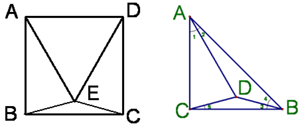
例34 原题:如图,正方形ABCD和正三角形ADE,求∠EBC的度数。
新题1、如图,等腰直角△ABC中,∠ACB=90度,∠1:∠2=2:1,∠4:∠3=2:1,∠5=∠3.求证:AD=AC.
新题2、如上题图,Rt△ABC中,∠ACB=90°,AC=BC,D在△ABC内,且AD=AC,∠CAD=30°,则∠DBC的度数是 。
两道新题都采用了“擦图”的手段编题。做题时要“补图”。
例35 原题:如图,正方形ABCD中,E、F在AD、AB上,∠ECF=45°,求证:BF+DE=EF。
新题:如图,梯形ABCE中,AB=BC=12,F在AB上,EF=10,∠ECF=45°, 求BF的长。
编题的方法同例34一样,新题解的方法是设BF=x,则AF=12-x,AE=12-(10-x)=2+x,在△AEF中用勾股定理列方程即可。
10、有新的发现而编题
当你对一些数学问题有自己独特的见解时,你就有了编题的思路,也许一道好题就这样诞生了。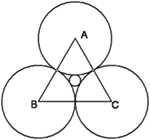
例36 大家一定见过这样的图形,三个等圆里面有一个小圆,我发现这四个圆是两两外切的。于是,就有下面这题:
已知有4个圆两两外切,其中3个圆的半径为6,(1)画出图形;(2)求第4个圆的半径。
例37 我在教三角形全等时,发现“边边角”有个有趣的现象:满足SSA的两个三角形如果不全等,那么这两个三角形的面积就相差一个等腰三角形的面积。
于是一道新题就诞生了: 已知\triangle{ABC}和\triangle{{A^\prime}{B^\prime}{C^\prime}}中,AB={A^\prime}{B^\prime}=8cm,BC={B^\prime}{C^\prime}=5cm,\angle{A}=\angle{A^\prime}=30°, 如果\triangle{ABC}和\triangle{{A^\prime}{B^\prime}{C^\prime}}不全等,则它们的面积之差是 cm^2.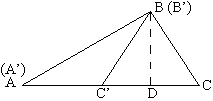
解法是:先画出图形,将两个三角形叠放在一起,作高BD,则可以算出BD=4,CC’=6,所以面积相差4×6÷2=12.
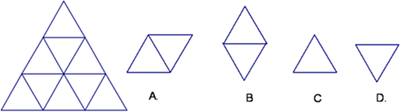
例38 我在用“画图”软件三角形网格时,先画一个三角形,然后进行“复制–粘贴–平移”共5次,一个3×3的三角形网格就形成了。于是就有了下题:
如图是一个由基本图形经过若干次平移后得到的图形,这个基本图形可以是( )
答案是C,但很多人想不到啊。
例39 发现一道错题,也许就发现了一道好题。下面的题就是错题改编的:
对于任意正整数n,(4n+5)^2-9一定可以被整数a整除,则a的值是 ( )
A、2 B、4 C、8 D、16
这是一道有问题的单项选择题,在不改变代数式和选择支的前提下,请你修改本题,使其成为一道无误的单项选择题.
答案:将“a的值是”改为“a的最大值是”。
例40 常见这样的题,已知方程组\left\{\begin{matrix}7x+3y=5\\3x-y=1\end{matrix}\right.,求x+y的值。
我们常用“整体思想”来解,即 (1)-(2),得4x+4y=4,所以x+y=1.
但是,若要求5x-y的值,整体思想就不好用了,有什么方法还能继续运用整体思想呢?后来我发现了方法。于是一道自己非常满意的代数题诞生了:
有这样一个数学问题: 已知x、y满足\left\{\begin{matrix}7x+3y=5\\3x-y=1\end{matrix}\right.,求x+y的值.我们可以用整体思想来解决这道题,由(1)-(2),得4x+4y=4,所以x+y=1.现在有一位同学想用同样的方法求5x-y的值,但他想不出上述两个方程如何运算的,请你写出获得运算过程的方法,帮助这位同学得到正确的解答.
平时我一旦有了编题的灵感,就会马上记录先来,现在我的收获颇丰,很多题在重大考试中采用,以上这些题贡献出来和大家分享,但是还有很多题从来没有公开过,就暂时保密了。
请参见我的另一篇博文“初中数学命题原则”。



《初中数学题的编制方法(续)》有一个想法