经典数学难题集锦

在这里，我会陆续展示一些平时收集的难题，供大家参考。我的解答可能不是最好的，请你指点。这些题目也不一定是难题，也不一定很经典，只能说这些题是我较喜欢的，喜欢的原因是我很佩服命题者。说不定今天你看到的这篇文章，已经比上次新增了几题。

例1

如图所示，一长方形被分割成9个互不交叠的正方形，如果该长方形的长与宽为互质的非零自然数，那么此长方形的周长为                      。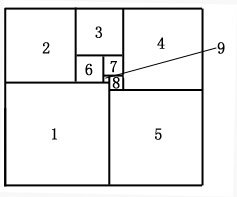

解：如图，设正方形6的边长为x，正方形7的边长为y，那么
正方形3的边长为x+y，
正方形2的边长为x+x+y=2x+y，
正方形9的边长为x-y，
正方形8的边长为y-(x-y)=2y-x，
正方形4的边长为(x+y)+y+(2y-x)=4y，
正方形1的边长为(2x+y)+x+(x-y)=4x，
正方形5的边长为(2y-x)+4y=6y-x或(2x+y)+4x-4y=6x-3y，
∴6y-x=6x-3y，y=\frac{7}{9}x，
∴长方形的两边长分别是(2x+y)+4x=6x+y=\frac{61}{9}x，4x+6y-x=3x+6y=\frac{23}{3}x，
为了使\frac{61}{9}x和\frac{23}{3}x互质，只能取x=9，这时边长为61和69，周长为260。

 

  例2

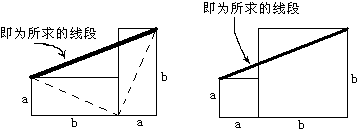
已知有一组邻边长为a，b的长方形两个，利用这两个长方形画出长为\sqrt{2a^2+2b^2}的线段。若已知的是边长分别为a，b的两正方形呢？

解：见下图。

 例3

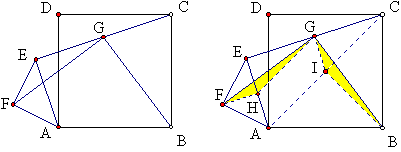
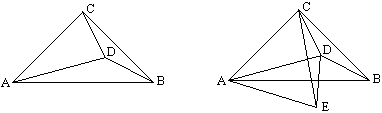
如图，正方形ABCD，△AEF是等腰直角三角形，∠EFA=90°，EC的中点是G，求证：GF=GB，GF⊥GB。

 

证明：如图，取AE、AC的中点H、I，则易证△FHG≌△GIB，所以GF=GB。证明GF⊥GB时，只要找到直线FH和GI的交点即可。

例4

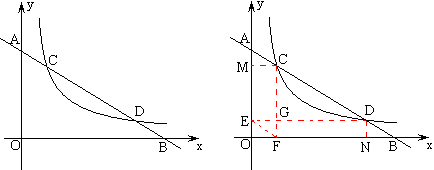
如图，一直线交y轴于A，交x轴于B，交双曲线于C、D，求证：AC=BD。

证明：如图，作矩形OEDN及矩形OFCA，DE和CF交于G，那么有

矩形CMEG的面积=矩形DNFG的面积，即有DG×GF=CG×GE，

也即\frac{DG}{GE}=\frac{CG}{GF}，这就说明AB∥EF，

所以四边形AEFC和四边形DEFB均为平行四边形，∴AC=EF=DB。

我们还可以将本题进行拓展，直线MC、直线ND、x轴、y轴围成一个矩形，这个矩形的一条对角线（即MN）平行于AB，另一条对角线必过点G。

例5

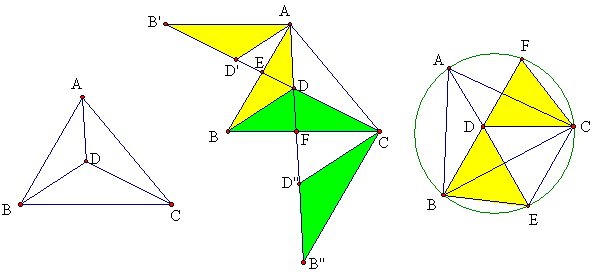
如图，点D是锐角△ABC的费马点，∠ABC=60°，AD=3，DC=4，求BD的长。

 

解：将黄色三角形绕A逆时针旋转60°至黄色位置，绿色也转60°至绿色位置，
所以AB’∥BC，AD’∥BD，B”C∥AB，D”C∥BD，
于是AB’:BC=AE:BE=AD’:BD，AB:B”C=BF:FC=BD:D”C，
即3：BD=BD：4，∴BD=2\sqrt{3}。

后来有一位同事解得较为简单：

如图，延长AD和BD，交△ABC的外接圆于E、F，则∠DEC=∠ABC=60°，∠EDC=60°，∴△DEC为正三角形，∵∠FDC=∠DCE=60°，∴BF∥EC，∴∠F=∠FBE，∵∠BDE=∠CDF=60°，∴黄色三角形全等，设BD=FD=x，由相交弦定理知x^2=3\times4，∴BD=2\sqrt{3}。

又后来我的徒弟说：这么简单的题，还需这么麻烦的方法？只要证明△ABD∽△BCD即可。

晕！我怎么了？原来，以前类似的图形是旋转的，这次掉进阴沟里了。

例6

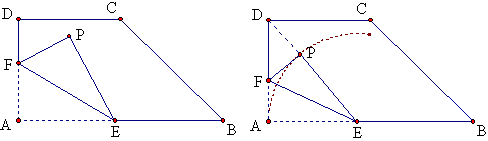
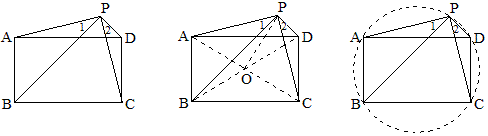
如图，直角梯形纸片ABCD，AD⊥AB，AB=6，AD=CD=3，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A落在P处。求PD的最小值。

解：先固定E点不动，则可知PE的长度不变（不论F点如何移动），所以P在以E为圆心AE为半径的弧上。这时当且仅当D,P,E三点共线时，DP最小。

设AE=x，DP=y，∵DP=DE-PE，∴y=\sqrt{9+x^2}-x，

变形得y=\frac{1}{\sqrt{9+x^2}+x}，

可见，当x越大时y就越小，∵x最大值是6，∴DP最小值是3\sqrt{5}-6。

例7

如图，四边形ABCD内接于圆，点M在AC上，∠1=∠2，∠3=∠4，求证：M是AC的中点。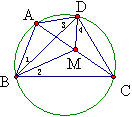

证明：∵∠1=∠ACD=∠2，∠3=∠ACB=∠4，∴△BMC∽△CMD，∴MC^2=BM{\times}MD，不难证明∠DMA=∠BMA，∠DAM=∠ABM，∴△ABM∽△DAM，∴AM^2=BM{\times}MD，∴M是AC的中点。

反思：

是不是任意圆内接四边形ABCD中，取AC中点M就会出现∠1=∠2，∠3=∠4？回答是否定是。这个图怎样画得？我的方法是：先画△ABC，再取中点M，连BM得∠2，作∠1使∠1=∠2得D点，即成。

于是就得到一个副产品：由上述作图可以证明∠3=∠4。但我没有深入思考如何证明。

例8

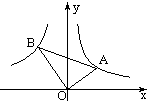
如图，点A在反比例函数\frac{\sqrt{3}}{x}的图象上，点B在反比例函数\frac{k}{x}的图象上，∠AOB=Rt∠，OA=2,OB=4，求k的值。

解：如图，过A,B作x轴的垂线，垂足分别为D,C，则△AOD∽△OBC，所以△AOD的面积：△OBC的面积=1：4，因为△AOD的面积=\frac{\sqrt{3}}{2}，∴△OBC的面积=2\sqrt{3}，∴k=-4\sqrt{3}.

 

例9

如图，等腰直角△ABC中，∠ACB=90°，D在三角形内，∠DCB=∠DBC=15°，求∠CAD的度数。

解：如图，沿CD将△CDB翻折B与E重合，连EC，易证△ACE是正三角形。又因为△ACD≌△AED，所以∠CAD=30°.

例10

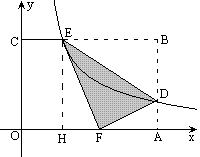
已知任意△ABC及三角形外一点P，过P点画一条直线，使这条直线平分三角形的面积。

如果你和我一样以前从未见过这题，恐怕很难想到用相似旋转变换来解决它。我们先来欣赏一下这不可思议的几何妙招：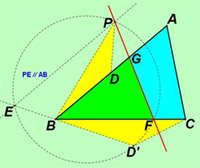

取AB的中点D，将△PBD绕点B进行相似旋转变换，得到△CBD’，过P作AB的平行线交D’B的延长线于E，过P、E、D’三点作圆，交BC于F，直线PF即为所求。

作为一个数学爱好者，看到论坛里这样精彩的讨论，怎能不心潮涌动、跃跃欲试呢？可惜我没能拥有这精彩的创造，但我又怎能失去一份解读它的荣耀？

如下图，让我们反过来分析，既然△GBF是△ABC面积的一半，可见它与△DBC等面积。去除公共部分不考虑，则△GDF与△CDF等面积，可见两个三角形同底等高，故GC∥DF。看来只要GC∥DF成立，证明便可完成。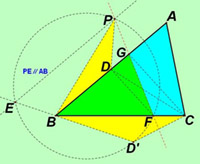

用什么方法来证明平行呢？试想，既然用到相似，当然用比例来证，就是说如果BD:BG=BF:BC成立，平行也就成立了。

看下图进一步我们的探究。

比例源于相似，我们肯定要研究两个黄色的相似三角形可以给我们提供什么比例式：BD:BD’=BP:BC。

观察比较一下我们需要的比例式可以发现什么？——两个比例式的外项是相同的！这就是说只要证到两个比例式中的内项积相等，即：BG·BF=BD’·BP，便大功告成！显然这个等积式是由比例式BG:BP=BD’:BF变来的，那这个比例式又该从何处来呢？

不难发现，它可由两个红色的三角形相似得来。换句话说只要你能证明红色三角形相似，你就可以揭晓谜底！

当我们看清了红色三角形为什么相似之后，我们才明白了那条平行线的精彩！那个圆的绝妙！！我们更看清了作图者的智慧，也更加领略到了数学世界的秀丽风光！

例11

一辆小车的前胎能跑500千米，后胎能跑300千米，问：在跑多少千米时换轮胎的行驶路程最长？

解：

方法一：设跑了x千米换轮胎，为使路程最长只要换了轮胎以后轮胎同时磨损完毕。又设汽车每个轮胎总磨损量为单位1。则有(1-\frac{x}{500})\div\frac{1}{300}=(1-\frac{x}{300})\div\frac{1}{500}，或1-\frac{x}{500}=\frac{x}{300}（两种方程含义不一样的，后一个方程要考虑到换轮胎前后的路程一样长，这是没有得到证明的），解得：x=187.5.

方法二：与方法一设一样的元，则得方程\frac{500-x}{500}\times{300}=\frac{300-x}{300}\times{500}，解得：x=187.5.

方法三：用小学的方法。设每一个轮胎总磨损量为单位1，那么不管换不换轮胎，前、后各一个轮胎跑1千米的磨损量为\frac{1}{500}+\frac{1}{300}，而前、后各一个轮胎总磨损量为单位2，所以一共可以跑2\div(\frac{1}{500}+\frac{1}{300})=375（千米），又换轮胎时已经开的路程为全程的一半（这是没有得到证明的），所以375÷2=187.5。有些人直接列式是：1\div(\frac{1}{500}+\frac{1}{300})=187.5（千米）。我始终不理解。

方法四：设每一个轮胎总磨损量为单位1，那么不管换不换轮胎，前、后各二个轮胎跑1千米的磨损量为\frac{2}{500}+\frac{2}{300}，所以4个轮胎一共可以跑4\div(\frac{2}{500}+\frac{2}{300})=375（千米），下面用“鸡兔同笼”来解。

假设375千米的行程都不换轮胎，则后轮多磨损了\frac{375}{300}-1，每1千米后轮换成前轮，可以少磨损\frac{1}{300}-\frac{1}{500}，

(\frac{375}{300}-1)\div(\frac{1}{300}-\frac{1}{500})=187.5（千米）。

例12

如图，P是矩形ABCD外一点，∠BPD=90°，连结AP、CP，求证：∠1=∠2.

解法1：连结AC、BD交于O，连PO。那么PO=\frac{1}{2}BD=\frac{1}{2}AC，∴∠APC=90°，∴∠1=∠2.

解法2：作矩形的外接圆，因为∠BPD=90°，所以P在圆上，∴∠1=∠2.

例13

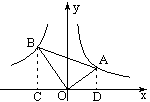
如图，矩形OABC中，点B（4，3），A、C在坐标轴上，双曲线y=\frac{k}{x}，交AB于D交BC于E，沿DE折叠，B落在x轴上一点F。求k的值。

解：容易求得AD=\frac{k}{4}，CE=\frac{k}{3}，

∴DF=DB=3-\frac{k}{4}，EF=EB=4-\frac{k}{3}.

为了列出方程，我们作EH⊥x轴于H，构造△EHF∽△FAD，∴\frac{EH}{FA}=\frac{EF}{FD}，即\frac{3}{\sqrt{(3-\frac{k}{4})^2-(\frac{k}{4})^2}}=\frac{4-\frac{k}{3}}{3-\frac{k}{4}}，运气不错，右边可以约简成\frac{4}{3}，最后解出k=\frac{21}{8}.

例14

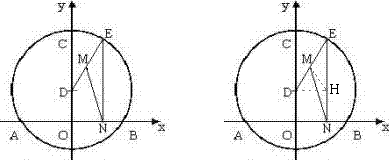
如图，在平面直角坐标系中，⊙D与坐标轴分别相交于A（-\sqrt{3}，0）B（\sqrt{3}，0），C（0，3）三点，E为优弧AB上一动点（不与A，B，C三点重合），EN⊥x轴于点N，M为半径DE的中点，连接MN，当∠DMN＝45°时，求E点的坐标。

解：作DH⊥EN于H，连接MH。容易计算圆的半径为2，则MH=DM=EM=1，HN=OD=1，∠MEN=∠MHE=2∠MNH=30°。因为DE=2，所以DH=1，EH=\sqrt{3}，∴E（1，1+\sqrt{3}），另一点是E（-1，1+\sqrt{3}）。

例15

已知a、b、c满足a^2+b^2+c^2=9，求(a-b)^2+(b-c)^2+(c-a)^2的最大值。

解：(a-b)^2+(b-c)^2+(a-c)^2 =a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2

=18-(2ab+2bc+2ac)=27-(a^2+b^2+c^2)-(2ab+2bc+2ac) =27-(a^2+b^2+c^2+2ab+2bc+2ac)=27-(a+b+c)^2

要取得最大值，只要(a+b+c)^2=0 就可以了。(如：a=0,b=-c)
所以这个最大值是27。

例16

如图，AB是\bigodot{O}的直径，CB切\bigodot{O}于B，CB=AB，CO交\bigodot{O}于E，直线AE交CB于D。求证：CE=DB。

解法1：连EB，由△CDE∽△CEB得，\frac{CE}{CB}=\frac{ED}{EB}，由△DEB∽△DBA得，\frac{DB}{AB}=\frac{ED}{EB}，又CB=AB，所以CE=DB。

解法2：延长EO交\bigodot{O}于F，连BF，

由△CEB∽△CBF得，\frac{CE}{CB}=\frac{CB}{CF}，

即CB^2=CE\times{CF}=CE\times(CE+EF)=CE\times(CE+CB)=CE^2+CE\times{CB}

由△CDE∽△CEB得，\frac{CE}{CB}=\frac{CD}{CE}，

即CE^2=CD\times{CB}

∴CB^2=CD\times{CB}+CE\times{CB}=CB\times(CD+CE)

即CB=CD+CE，∴CE=DB。

解法3：在AE上取一点F，使BF=BD，易证∠CBE=∠FAB，∠BEC=∠AFB，又CB=AB，∴△AFB≌△BEC，∴BF=CE，即CE=DB。

例17

计算\frac{1}{1\times3}+\frac{2^2}{3\times5}+\frac{3^2}{5\times7}+\cdots\cdots+\frac{1004^2}{2007\times2009}.

解：因为分子乘以4均比分母大1，

所以原式=\frac{1}{4}(1+\frac{1}{1\times3}+1+\frac{1}{3\times5}+1+\frac{1}{5\times7}+\cdots\cdots+1+\frac{1}{2007\times2009})

=\frac{1}{4}[1004+\frac{1}{2}(1-\frac{1}{2009})]=251\frac{251}{2009}.

例18

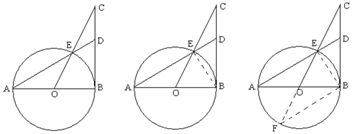
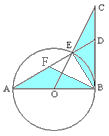
如图，半圆直径AB=2，CD⊥AB于D，CD=2，CB交半圆于E，AE交CD于H，求OH+HD。

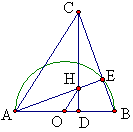
解：设OD=x，则AD=1+x，DB=1-x，由△AHD∽△CBD得：

HD=\frac{1-x^2}{2}，HO=\frac{1+x^2}{2}，

所以OH+HD=1.