在《经典数学难题集锦1》里已经收集了18道难题,现在再给大家展示几题,一起共享。
例19
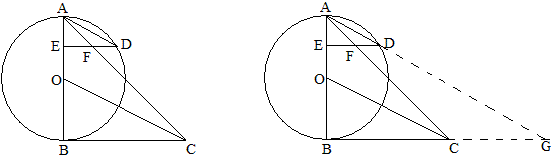
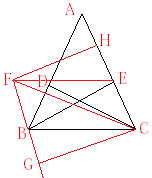
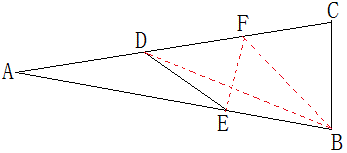
如图,AB是⊙O的直径,C在圆外,D在圆上,AD∥CO,CB⊥AB,DE⊥AB于E,AC交DE于F,求证:EF=FD。
解:如图,延长AD、BC交于G,易证OC是△ABG的中位线,所以BC=CG,因为ED∥BG,由比例线段可以证明EF=ED。
例20
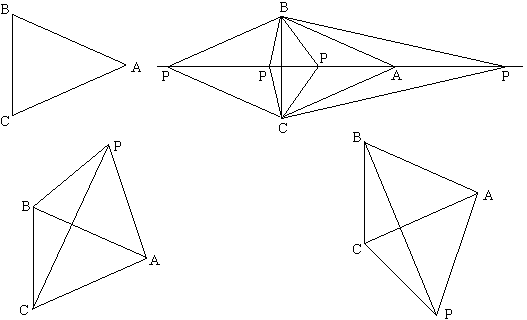
如图,等腰三角形ABC中,AB=AC,∠A是锐角,找一点P,使△PAB、△PAC、△PBC均为等腰三角形,这样的点P共有几种不同的位置?
解:如图,一共有6种。
例21
如图,\triangle{ABC}\sim\triangle{AEF},其中∠BAC=∠FAC,∠BCA=∠AFE。求证:AB×CF=AC×BE。
解:由已知,得\frac{AB}{AC}=\frac{AE}{AF},加上条件∠BAC=∠FAC,得\triangle{ABE}\sim\triangle{ACF},所以\frac{BE}{CF}=\frac{AE}{AF},等量代换后得\frac{AB}{AC}=\frac{BE}{CF},即AB×CF=AC×BE。
例22
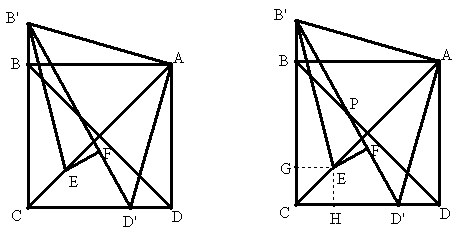
如图正方形ABCD中,∠B'AD'=90°,交正方形的边或延长线于B',D',∠CB'D'的平分线交AC于E,EF⊥B'D'于F,求证:BC-EF=\frac{1}{2}B'D'.
解:如图,作EG⊥BC于G,EH⊥CD于H,易证BB'=DD',EG=EH=EF,B'G=B'F,D'F=D'H,所以2BC=BC+DC=B'C+D'C=B'D'+2CH=B'D'+2EF,
故2BC-2EF=B'D',即BC-EF=\frac{1}{2}B'D'.
顺便一提:我们还能证明P是B'D'的中点,BG=B'P。
例23
已知实数a、b、c满足a+b+c=0,且a>b>c,求\frac{a}{c}的取值范围。
解:由已知a>0,c<0.对b进行分类讨论。
当b>0时,设a=nb(n>1),则\frac{a}{c}=\frac{-b-c}{c}=-\frac{b}{c}-1
因为-c=a+b=(n+1)b,所以\frac{a}{c}=\frac{1}{n+1}-1
因为n>1,故-1<\frac{a}{c}<-\frac{1}{2}.
当b<0时,设c=nb(n>1),则\frac{a}{c}=-\frac{b}{c}-1=-\frac{1}{n}-1
因为n>1,故-2<\frac{a}{c}<-1.
当b=0时,a=-c,故\frac{a}{c}=-1.
综上所述:-2<\frac{a}{c}<-\frac{1}{2}.
另一种方法:
设\frac{a}{c}=k,则a=ck,b=-(k+1)c,代入已知得ck>-(k+1)c>c,注意到c<0,
可解得-2<k<-\frac{1}{2},即-2<\frac{a}{c}<-\frac{1}{2}.
例24
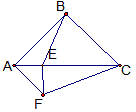
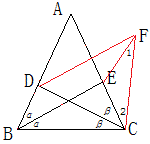
设△ABC中,CD、BE分别是角平分线,CD=BE,证明:△ABC是等腰三角形。
证明: 作∠BEF=∠BCD;并使EF=BC,
∵BE=DC,∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF,
设∠ABE=∠EBC=α,∠ACD=∠DCB=β,
∴∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);
∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);
∴∠FBC=∠CEF,
∵2α+2β<180°,∴α+β<90°,∴∠FBC=∠CEF>90°,
∴过C点作FB的垂线和过F点作CE的垂线必都在FB和CE的延长线上.
设垂足分别为G、H;∠HEF=∠CBG;
∵BC=E,∴Rt△CGB≌Rt△FHE,∴CG=FH,BG=HE,连接CF
∵CF=FC,FH=CG,∴Rt△CGF≌△FHC,
∴FG=CH,∴BF=CE,∴CE=BD,
∵BD=CE,BC=CB,∴△BDC≌△CEB,∴∠ABC=∠ACB,∴AB=AC。
解法二:
如图,作平行四边形DBEF,连FC,用反证法如下:
假设AB<AC,∠ABE=∠EBC=∠DFE=α,∠ACD=∠DCB=β,则α>β,
∵DF=DC,∴∠DFC=∠DCF,∴∠1<∠2,∴BD=EF>EC,
另一方面,在△BCD和△CDE中,有两边对应相等,则夹角大的对边也大,
可知EC>BD,这与BD>EC矛盾,∴AB<AC错误,同理AB>AC也错误。故AB=AC。
例25
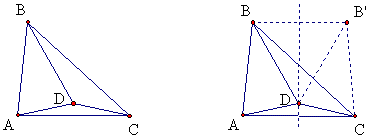
如图,△ABC中,∠BAC=2∠BCA,D在三角形内,DA=DC,BD=BA,求证:∠ABC=3∠DBC。
证明:
如图,作B的对称点B’,则BC平分∠B’CA,
∵BB’∥AC,∴∠B’BC=∠BCA=∠BCB’,
∴BB’=B’C=AB=BD,故△BB’D为正三角形。
设∠BCA=∠B’BC=α,则∠DBC=60-α,∠ABC=180-3α,
故∠ABC=3∠DBC。
备注:
1、本题是下面这道题的拓展
已知△ABC是等腰直角三角形,∠BAC=90°,D在三角形内,DA=DC,BD=BA,求∠DBC的度数。
解题方法是补全一个正方形。
2、本题还有一个结论:∠BCD=30°。
3、点D不一定在三角形内,也可以在AC的下方,结论依然成立。
例26
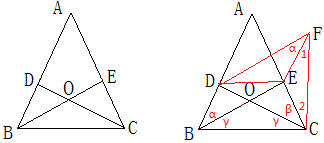
如图,△ABC中,O是形内一点,OB=OC,射线CO,BO分别交AB,AC于D,E,且AD=AE。求证:△ABE≌△ACD。
证明:
如图,作平行四边形DBEF,连FC、DE,为了证明AB=AC,用反证法如下:
假设AB<AC,∠ABE=∠DFE=α,∠ACD=β,∠OBC=∠OCB=γ,则α+γ>β+γ,α>β,
∵AD=AE,∴EF=BD<EC,∴∠1>∠2,∴∠DFC>∠DCF,∴DC>DF=BE,
故OD>OE,∠OED>∠ODE,即∠OEA>∠ODA,
∵∠OEA=β+2γ,∠ODA=α+2γ,∴β+2γ>α+2γ,即β>α,这与α>β矛盾,其余不难证明。
例27
如图,△ABC中,AB=AC,D、E在AC、AB上,且AD=DE=EB=BC,求∠A的度数。
解:作∠ABC的角平分线BF,连EF、BD,易证△BCF≌△BEF,设∠A=∠AED=x度,则∠EDC=2x,∠EDB=∠EBD=x/2,
于是可证∠FEB=∠C=∠FED=90-x/2,∴△DEF≌△BEF,∴∠DFE=60度,故∠A=20度。
例28
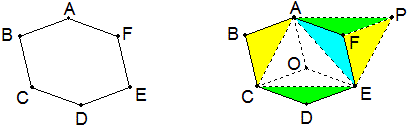
如图,六边形ABCDEF中,6条边均相等,∠A+∠C+∠E=∠B+∠D+∠F,求证:∠B=∠E。
证明:
将黄色三角形、绿色三角形和蓝色三角形拼到一起,组成△AEP,易证F是△AEP的外心,且△ACE≌△EPA。
设O是△ACE的外心,则得三个菱形AOCB,COED,EOAF,这样就不难证明∠B=∠E。