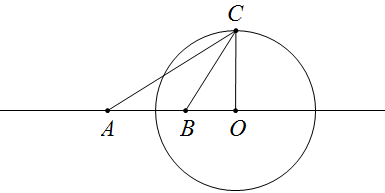
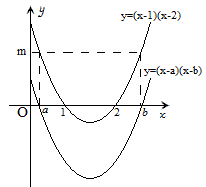又称阿波罗尼斯圆,已知平面上两点A、B,则所有满足PA/PB=k且不等于1的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆。
分类: 解题技巧
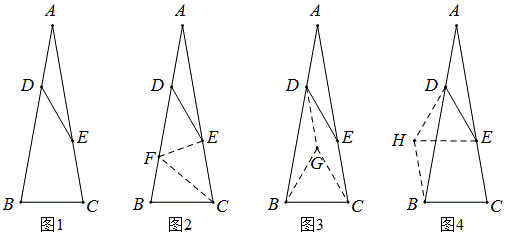
三角形中的角格点问题
如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都是10的倍数,我们称这样的点为三角形中的格点.求解三角形中的格点问题,常可利用对称点.利用对称点求解三角形中的格点问题,方法简单易行,解法简洁巧妙,题面新颖有趣,是学生巩固知识,培养能力,陶冶情操,提高素质的宝贵资料.
证明角格点的方法是作轴对称图形,即构造轴对称的全等三角形。
不一样的解法,不一样的效果
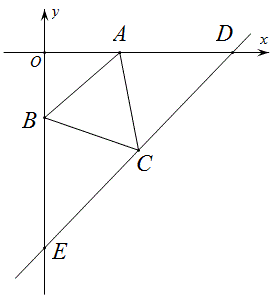
问题:如图,正三角形ABC中,A(4,0),B(0,-2\sqrt{3}),D(10,0),求直线DC的解析式。
请看下面四种解法,各有巧妙不同,运算量大小不一,你更喜欢哪种?
老封研究过的几何题
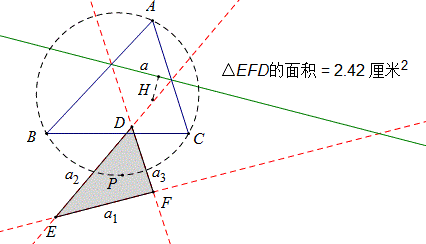
叶中豪提出了如下几何问题:
如图,H是△ABC的垂心,直线a是任意的一条直线,直线a_1、a_2、a_3是直线a关于BC、AC、AB轴对称直线。三条对称直线围成△DEF。
(1)何时D、E、F共点?实验发现直线a过H时共点。
(2)△DEF的面积由H到a的距离决定。
(3)△DEF的内心P在△ABC的外接圆上。
(4)当直线a位置变化时,△DEF的形状不变。
几个互逆命题的证明
一、原命题
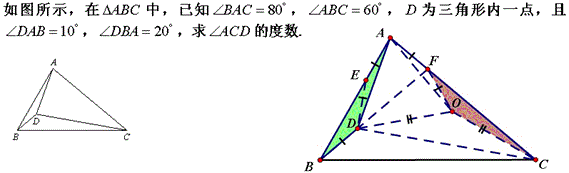
如图,△ABC中,AB=AC,∠A=100°,BD为角平分线,求证:BC=BD+AD.
解:将点A 沿BD反射至BC上的E点,在BC作BF=BD,那么易证DE=DF=CF,
所以BC=BD+AD.
一道几何题的多种证明方法
问题:如图1,△ABC中,AB=AC,D,E分别在AB,AC上,且AD=DE=EC=BC,求证:∠A=20°.
解法1:如图2
作∠ACB的角平分线CF,连EF,那么△BCF≌△ECF,设∠A=x°,于是∠B=∠FEC=90-\frac{1}{2}x,
∠DEF=180-x-(90-\frac{1}{2}x)=90-\frac{1}{2}x=∠FEC.
∴△DEF≌△CEF,∴∠BFC=∠EFC=∠EFD=60°,
在△BFC中,∵一个角为60°,另两个角是2倍关系,∴∠B=80°,∴∠A=20°.
几何中的基本模式(续)
四、四边形中的基本模式
1、正方形
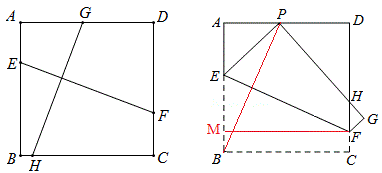
(1)正方形中的垂直线段
如图,在正方形ABCD中,EF⊥GH,那么EF=GH,反之亦然
例16 如图所示,现有一张边长为7的正方形纸片ABCD,点P为正方形AD边上的一点,AP=3,将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,求FG的长。
解:连BP,作FM⊥AB于M,由上模式,因为BP⊥EF,所以△ABP≌△MFE,所以ME=AP=3,
设GF=CF=MB=x,那么EP=EB=3+x,AE=4-x,由△AEP中的勾股定理得,(3+x)^2=(4-x)^2+3^2,
解得x=\frac{8}{7}。
注:连结PF利用两个直角三角形的公共斜边,解法更为简单。
几何中的基本模式(待续)
想加快解几何题的速度,就要牢记常见的几何命题的图形、条件和结论。我把它叫做“几何基本模式”。
“基本模式”虽然不是定理,虽然不能在证明过程中直接应用,但其作用不亚于定理,至少我们可以在填空题、选择题中加以应用,还可以运用它进行问题的分析,作为推理的依据,看清解题思路,加快思维速度。几何基本模式就是我们解题的经验,模式记得越多经验就越多。下面举例一一加以说明。
利用函数图象解决数学问题
有许多数学问题,用函数图象解决优于其它方法, 而这恰恰是许多人想不到的。究其原因是缺乏函数思想和数形结合思想。
我相信,当你看完以下题目的解答后,一定会收到启发,利用函数图象解决问题的方法便会成为你有力的工具。
一、函数图象解决方程问题
例1 已知关于x的一元二次方程(x-1)(x-2)=m(m>0)的两个解分别是a和b,那么关于x的一元二次方程(x-a)(x-b)+m=0的两个解是什么?
解:构造三个函数如下:
y_1=(x-1)(x-2),y_2=(x-a)(x-b),y_3=(x-a)(x-b)+m,前两个函数图象如下:
由图可知,函数y_2=(x-a)(x-b)的图象可以看作是函数y_1=(x-1)(x-2)图象向下平移m个单位得到的。
再将函数y_2=(x-a)(x-b)的图象向上平移m个单位就得到y_3=(x-a)(x-b)+m,也就是y_1=(x-1)(x-2),
所以一元二次方程(x-a)(x-b)+m=0的解就是(x-1)(x-2)=0 的解,即解为x_1=1,x_2=2.
数学群问题讨论汇总5
前面已有4篇汇总:
问题42
黄冈朱老师的解答:
延长BD交AC于F,作A关于BF的对称点O,AD的垂直平分线交AB于E点。