寻找全等三角形对应关系的方法–204班周涛

我们已经学习了全等三角形，全等三角形最重要的是找对应关系，如果图形还简单的话，那就容易找，如果遇到较复杂的图形就很会看错，找对应位置就很会出错。要是你看了以下几种方法，肯定会使你熟练地找到对应关系，能找对应关系后才可以正确地判断全等三角形，因此找对应关系十分重要。我现在为大家提供几种方法，以供参考。

1、由已知的对应位置找对应关系

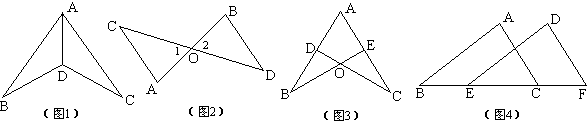
这是指如果两个三角形全等，如图1△ABD≌△ACD，所以就可以按字母的对应位置来找对应边和对应角，如A和A都排在第一位，B和C都排在第二位，D和D都排在第三位，那就可以得出∠ADB和∠ADC对应，其它的角和边也这样对应。

2、相等的角是对应角，相等的边是对应边

如图1，AD是公共边，就一定是对应边。如图2，∠1和∠2是对顶角，就一定是对应角。一般的，对顶角、公共角、公共边、平行线的同位角等都是对应元素。

3、由已知的对应元素找其它对应元素

对应边的对角是对应角，对应角的对边是对应边，两个对应角的夹边是对应边，两个对应边的夹角是对应角。

如图2，△AOC≌△BOD，AC∥BD，则∠A=∠B是对应角，它们的对边CO和DO就是对应边。如图3，△ABE≌△BCD，∠B=∠C，那么∠A、∠B的夹边AB和∠A、∠C的夹边AC是对应边。

4、由图形变换找对应关系

将一个三角形通过运动与另一个三角形重合，从而找到对应关系。有三种变换方法。

（1）旋转

这就是一个三角形绕某点旋转一定角度后与另一个三角形重合，如图2，△BOD可以绕点O旋转180°，与△AOC 重合，于是重合的元素就是对应元素。

（2）翻折

如图1和3，都可以经过翻折使两个三角形重合。

（3）平移

如图4中的两个三角形经过平移可以重合，重叠的角、边就是对应角、对应边。

上述所介绍的都是一些比较常用的找对应关系的方法，其中以变换方法最为重要。实际上我们遇到的图形比这里展示的图形复杂得多，想象把一个图形挖出来，通过“转”、“翻”、“移”等方法放到另一个三角形上去，这种方法能起到很好的作用。希望大家能利用这些方法，使我们熟练找到对应关系，为全等三角形的学习，也为相似三角形的学习打好基础。