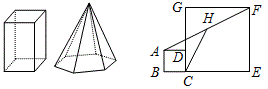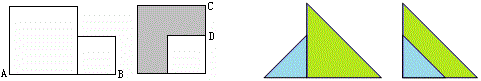今年中考前,许多老师纷纷研究我的命题习惯、思路和理念,有人还整理出比较系统的一整套资料。企图从中猜题,结果都失望了。
命题,尤其是中考命题,我们往往有如下的命题理念。
1、送分到家;2、新颖;3、应用性;4、考查核心知识;5、考查能力;6、问题要有鲜活的背景;7、让搞题海战术的人占不了便宜;8、多年不考的核心知识必考。
如果要说有什么原则,我比较关注的原则有:
科学性;新颖性(赋予问题背景);适应性(难度系数,课标要求,学生实际);时代性(分类,新定义,综合性,操作题);特色性(地方特色,社会热点);学科性(思维,能力,PISA,数学思想和方法);公平性(多一点新面孔,让题海战术失灵)
一、新颖性
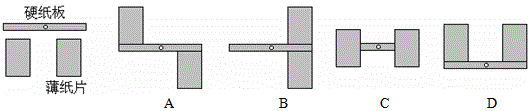
例1 (14年中考宁波第3题)用矩形纸片折出直角的平分线,下列折法正确的是
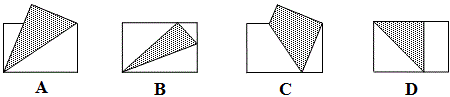
按照许多命题者的习惯,中考卷中都会放一道考对称性的选择题,给出4个图形,如各种各样的标志、图标、logo。
像上面第3题,虽然也是4个图形,但却来自于平时学生的错误,接地气啊。同样的试题我还编过如下一题:
例2 风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是
二、考查核心知识
核心知识很多,但有些会被遗漏,而且会连续很多年被遗忘,如反例、配方在宁波就这样。
例3 (14年中考宁波第9题)已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是
A.b=-1 B.b=2 C.b=-2 D.b=0
举反例说明一个命题是假命题,这是一种能力(推理),全国各地中考试卷从没有涉及,为什么命题人这么不重视反例呢?关于反例还可以这样命题:
例4 说明命题“如果是△ABC的三边,那么长为的三条线段能构成三角形”是假命题的反例可以是
A.a=2,b=2,c=3 B.a=2,b=2,c=2
C.a=2,b=2,c=4 D.a=3,b=4,c=5
例5 (14年中考宁波第12题)已知点A(a-2b,2-4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点的坐标为
A.(-3,7) B.(-1,7) C.(-4,10) D. (0,10)
配方法是初中及其重要的方法,但10年来宁波都没有考到,关于配方我曾命过如下题目:
例6 已知二次函数的图象过(0,-6)、(1,0)和(-2,-6)三点.
(1)求二次函数解析式;
(2)求二次函数图象的顶点坐标;
(3)若点A(m-2n,-8mn-10)在此二次函数图象上,求m、n的值.
例7 已知a,b是实数,且满足a²+b²=2a-2b-2=k,则k= 。
三、公平性
中考卷中新面孔要多,但不是新面孔就难,公平性就体现在大家都没有见过,让靠题海得分的人失效,这是中考命题的理念。
例8 (14年中考宁波第10题)如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
例9 (14年中考宁波第11题)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
A.2.5 B. C. D.2
例8源自我的发现:n棱柱有3n条棱,n棱锥有2n条棱。
例9的编题过程是这样的:
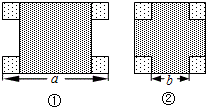
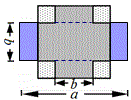
例10 (14年中考宁波第16题)一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 ▲ (用a,b的代数式表示).
因式分解都是送分题,但我想改变这个习惯,因式分解为什么一定要送分呢?用几何背景出因式分解的题是一种尝试。本题至少有3种方法,入口宽。
解法1:设大正方形边长为x,小的为y,那么x+2y=a,x-2y=b,算出两种正方形的边长,再求x2-4y2即可。
解法2:几何方法—-割补
解法3:因式分解法
设大正方形边长为x,小的为y,那么x+2y=a,x-2y=b,则S=x2-4y2=(x+2y)(x-2y)=ab.
本题还可以这样改编:
四、应用性
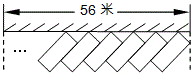
例11 (14年中考宁波第17题)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 个这样的停车位.(\sqrt{2}≈1.4)
解析:停车难是当今社会热点问题。所谓强调背景,这就是背景。56这个数据讨论许久,能被1.4整除,计算量小了。本题可以这样解:
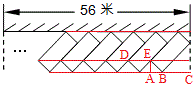
如图,按中间一条红色辅助线来计算,结果正确:
车位数=\dfrac{56-AB-BC}{DE}+1=\dfrac{56-1.1\sqrt{2}}{2.2\sqrt{2}}+1≈17.54≈17(\sqrt{2}≈1.4).
按上面红色辅助线来计算,结果错误:
车位数=\dfrac{56-1.1\sqrt{2}}{2.2\sqrt{2}}+1≈18.68≈18(\sqrt{2}≈1.4).
按下面红色辅助线来计算,结果错误:
车位数=\dfrac{56-2.5\sqrt{2}}{2.2\sqrt{2}}+1≈18.05≈18(\sqrt{2}≈1.4).
停车位问题如果设想这样画图,将更难。
五、旧貌变新颜
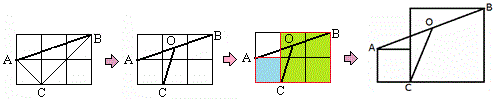
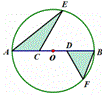
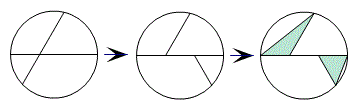
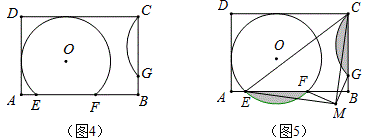
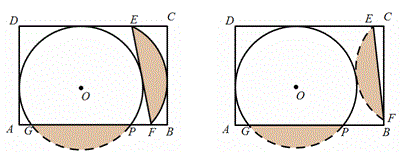
例12 (14年中考宁波第18题)如图,半径为6的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF.则图中两个阴影部分的面积和为 .
本题的编题过程如上图所示。将下方的三角形DBF反射到△ACE下方,那么就可以利用三角形面积公式进行计算。
六、书本题改编
教材中有这么一道题:
用白铁皮做盒子,每张铁皮可裁剪12个盒身,或18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
该题有问题,一是存在性,每张铁皮可裁剪12个盒身或18个盒盖,存在这样的裁剪方法吗?二是“盒身”概念不明确。但这题的背景可以利用,于是就有了下面一题:
例13 (14年中考宁波第24题)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
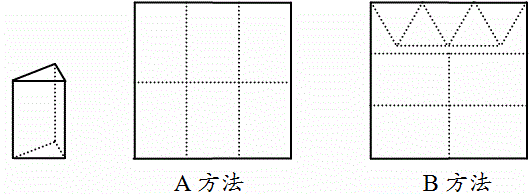
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
本题叙述清楚,概念明白,操作性强,解题方法简单。过去常用的行程问题、工程问题、调配问题等应用题已经渐渐退出历史舞台,取而代之的是有新颖背景的、实实在在可操作的应用题。书本中无盖盒子的应用题开创了这类应用题的先河。
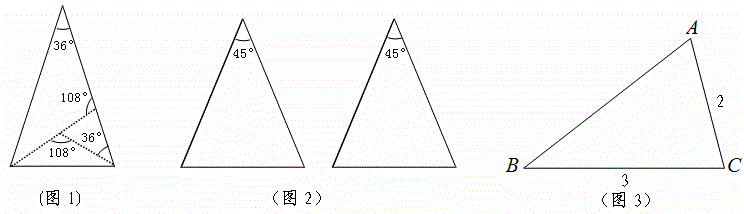
例14 (14年中考宁波第25题)课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.你能办到吗?请画示意图说明剪法.
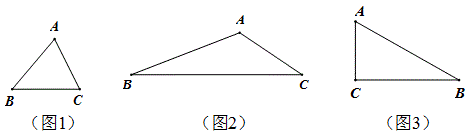
我们有多种剪法,图1是其中的一种方法:
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
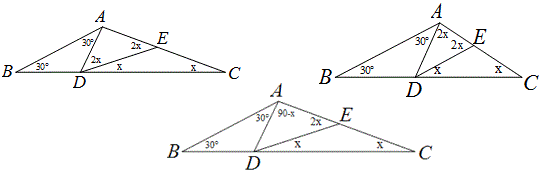
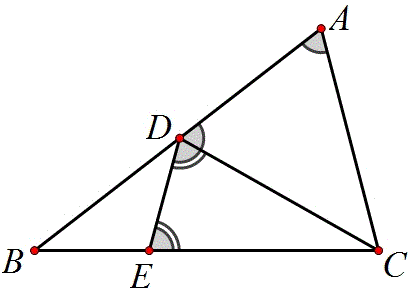
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在边BC上,点E在边AC上,且AD=BD,DE=CE.设∠C=x°,试画出示意图,并求出x所有可能的值;
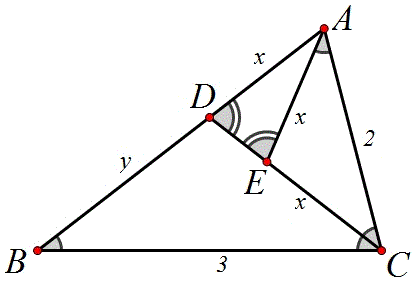
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的一种三分线,并求出三分线的长.
自定义题是近年来宁波中考数学的传统,结合书本题目出题是受到好评的。
25(2)试题中要不要给出图形,有过一番争论。但最终没有给出图形,难度上去不少。这题的解答要分3类讨论,分类讨论是初中数学的重要数学方法,每年中考必考。
当AE=AD时,得2×30°+180-4x+x=180,解之x=20°,
当AD=DE时,得2×30°+2x+x=180,解之x=40°,
当DE=AE时,得2×30°+90-x+x=180,无解。
25(3)有3种画法,命题意图只要求画出一种,并求出三分线的长度。
方法一:
如上图,作角平分线CD作AE=AD,则由△ADC∽△ACB,得22=x(x+y),又△AEC∽△ADC,得x:y=2:3,解之x=\frac{2}{5}\sqrt{10},y=\frac{3}{5}\sqrt{10}.
方法二:
如上图,作CD=CA=CE,易证EB=ED,故CD=3,DE=1.
方法三:作角平分线AE,
本题也可以这样设计:
例15 如果一组线段将一个三角形分割成n(n为大于1的整数)个等腰三角形,我们称这组线段为这个三角形的n分线.如等边三角形的三条中位线是它的4分线.
(1)直角三角形斜边上的什么线是它的2分线?
(2)如图1,△ABC是锐角三角形,在三角形内找一点P,使PA、PB、PC是它的3分线,并指出P是△ABC的什么点;
(3)①如图2,△ABC中,∠C=α度,∠B=(90-2α)度,0<α<45,请画出△ABC的3分线;
②如图3,△ABC中,∠ACB=90°,BC >AC,请画出△ABC的3分线.
还可以这样出题:判断下列命题是否正确(都是真命题哦)
(1)直角三角形一定有n分线(n≥2,n为整数)
(2)锐角三角形一定有n分线(n≥3,n为整数)
(1)钝角三角形一定有n分线(n≥4,n为整数)
七、夺人眼球的压轴题
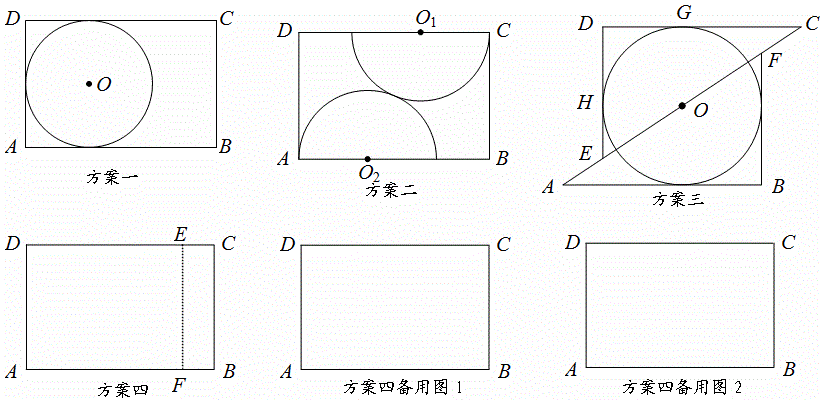
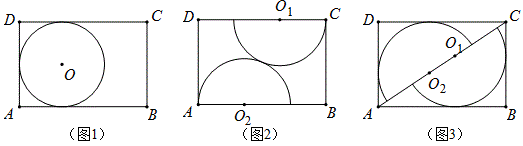
例16 (14年中考宁波第26题)木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面.他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1,O2在AB,CD上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
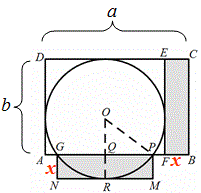
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的整圆.
(1)写出方案一中圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.
压轴题不考函数图象在去年各地中考命题中已经发出一个信号。
13年的安徽、哈尔滨、大庆考四边形,厦门考一元二次方程,广东考三角形重叠面积,河北、无锡考棱柱,常德、娄底、南京考三角形,长春、青岛考动点,连云港考面积最值……
13年浙江:杭州正方形,台州“好玩三角形”,宁波圆+坐标系,温州平行四边形+坐标系,丽水三角形+坐标系。
14年各地中考数学卷的压轴题:
安徽:正六边形; 大庆:圆内接梯形; 哈尔滨:四边形; 长春:矩形;
广州:梯形; 广东:等腰三角形; 佛山:三角函数; 河北:正方形+行程问题;
咸宁:正方形+坐标系; 娄底:直角三角形; 常德:正方形; 常州:圆+坐标系;
连云港:正方形+动点; 南京:SSA; 宿迁:三角形+坐标系; 扬州:矩形;
徐州:矩形+圆; 青岛:菱形+动点; 淄博:圆+坐标系。
14年浙江各地:湖州:圆+坐标系;绍兴:三角形+坐标系;温州:平行四边形+坐标系;台州:等角六边形;宁波:矩形和圆(生活实际问题)。
离开坐标系的压轴题必经少数,却是一个方向。结合生活实际的压轴题几乎没有。我要为世人证明实实在在的生活实际问题也可以作为压轴题,只不过这需要生活和数学的多年积淀。
我是木匠出身,做过圆台面,一块三夹板如何做圆台面呢?我曾经设计过本题提到的4种方案,并用方案3的方法用一张三夹板(宽122cm,长244cm)为老妈做了一张能坐12人的圆台面。但方案4的方法只是看见别人这样做过,心里总是困惑:到底是方案3的半径大?还是方案4的半径达?悬而未决的困惑留在心里近40年,直到今年中考前,为了命制本题,在几何画板中进行了探究:
第(3)题的解答是这样的:
其实当x=\frac{1}{2}时最大的圆是否能画是要检验的。如图r=\frac{5}{4},OP^2=OQ^2+OP^2=(\frac{5}{4}-\frac{1}{2})^2+1^2=\frac{25}{16}=r^2,说明圆经过P点。
探究一下一般情形:矩形一边a,一边b(a>b),割下的宽为x,
那么a-x=b+x,x=\frac{a-b}{2},r=\frac{b+x}{2}=\frac{a+b}{4},
OP^2=OQ^2+OP^2=r^2,(\frac{a+b}{4}-\frac{a-b}{2})^2+(\frac{b}{2})^2=(\frac{a-b}{2})^2,
化简得a:b=3:2.
本题初稿是这样的,后因篇幅过长进行了修改。
情景展现
黄木匠用长AB=3,宽BC=2的矩形木板做一个圆台面.他想如果直接锯下一个完整的圆,直径只有2(如图1).如果锯下两个半圆拼成一个圆,直径会大一些.于是他设计了两种方案:
方案1:如图2,圆心O1、O2在AB、CD上,半径分别是O1C、O2A,画两个外切的半圆;
方案2:如图3,沿对角线AC将矩形木板分成两个直角三角形,在每一个三角形内画出最大的半圆.
问题解决
(1)方案1中圆的半径长是 ;方案2中圆的半径长是 .
深入探究
黄木匠又想,如果锯下两个弓形拼成一个圆,情况又如何呢?于是又他设计了一个方案.
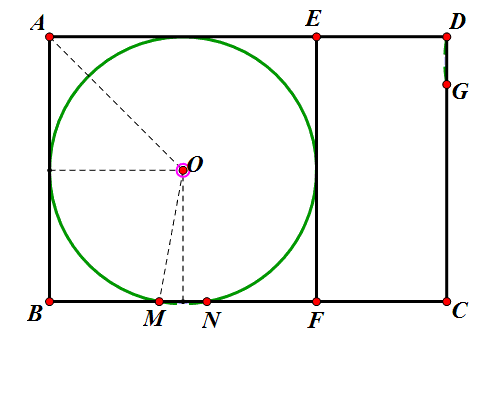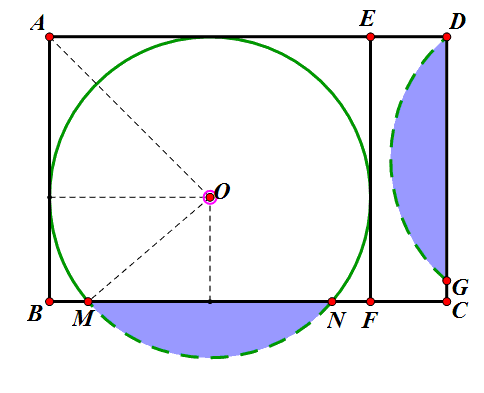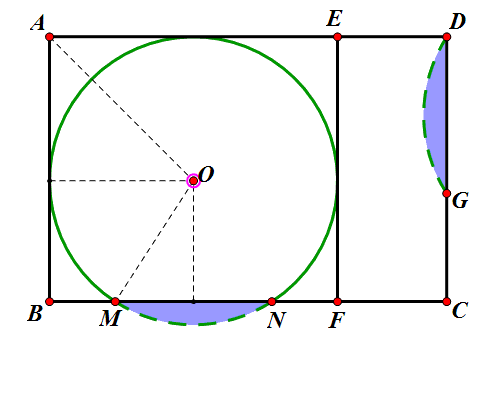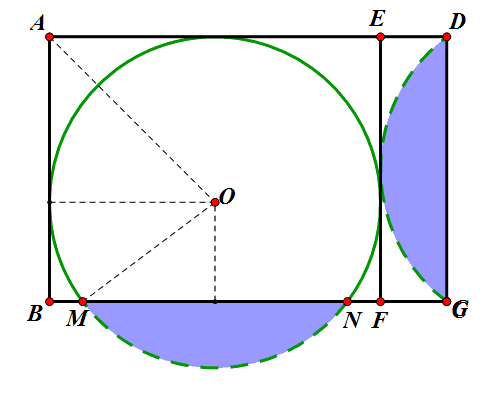
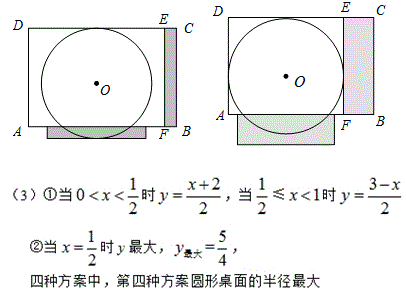
方案3:如图4,画一个比半圆大的弓形(称为优弓形),分别与AD、DC相切,圆心为O,弦EF在AB上.再在矩形剩余部分画一个比半圆小的弓形(称为劣弓形),弦CG在CB上,优弓形和劣弓形正好能拼成一个圆.
如何画出劣弓形呢?如图5,以EC为斜边作等腰直角△CEM,以M为旋转中心,顺时针旋转90°,矩形外的劣弓形就被变换至矩形内了,这是为什么呢?问题归结为下面的证明.
(2)求证:FM=GM,FM⊥GM.
最后结论
(3)设方案3中优弓形的半径为x,GB=y,
①写出y关于x的函数解析式;
②显然当y=0时圆的半径最大,那么三个方案中圆台面半径哪个最大?
本题还可以再探究:如果劣弓形画成如图的位置,情况又如何呢?
2014年《中学数学教学参考》第9期的中考频道栏目刊出了一篇文章,题目是
《情境朴实 知识关联 推理严谨》–宁波卷第26题分析,作者是台州命题专家李梦虎。他对本题进行了细致的剖析,指出本题的亮点,可谓我的知音。