遵循学生认知规律，提高课堂教学效益

心理学的研究表明，学生在学习知识、技能的过程中遵循一定的认知规律。遵循学生的认知规律，让学生在符合自身认知规律的教学活动中成长，这样的教学才会变得更有效。

某些学校某些老师，不是设身处地为学生着想，遵循他们的认知规律，而是“二节新课一节上，没有学过先要考，个个来做竞赛题，学生都把神仙当”。尤其是一些重点中学，许多好学生就这样厌学了，身心受到极大的创伤，这种效应还波及到父母。大多数教师没有这样离谱，但还是有人对学生认知规律把握不准，教学难度、广度、深度、梯度模糊不清，教学方法、教学模式选择有误，课堂结构安排不合理，使得学生学习困难。如果我们每一个教师能转换角色，常常想一个问题：“我要是作为学生，听自己的课，哪里会有困难？”那么他一定是个好教师。

可以这样说，我的成功离不开这个想法。我读初一的时候，数学老师上课上得我云里雾里，为什么要学有理数？为什么要叫有理数？为什么要这样算有理数？种种困惑使我对数学失去学习的兴趣。我当老师的第一个承诺是：“我绝不做我初一的数学老师。” 如何遵循学生的认知规律，我的做法供大家参考。

1、讲授概念通俗易懂

初中生的心理特征和认知规律告诉我们，他们的形象思维比抽象思维更完善，抽象思维还有待于继续发展，抽象程度还不能太高。所以教师常常需要借助图形、图象、类比、举例、枚举、特殊到一般等方法进行教学，这就是为什么要在初中阶段提倡轻概念重能力的原因。

例如：

（1）直线和圆的位置关系

本课可以用类比方法来进行教学，教师先画出如下表格（右边的内容暂不列出）进行复习：

名称	三角形的外接圆	三角形的内切圆
定义	经过三角形三个顶点的圆叫做三角形的外接圆	和三角形三边都相切的圆叫做三角形的内切圆
圆心的名称	外心	内心
圆心的产生	两边中垂线的交点	两条角平分线的交点
性质	外心到三角形的三个顶点距离相等	内心到三角形的三边距离相等

然后用类比的方法逐条添加表格右边的内容。

（2）一次函数的图象

传统的引入是描点法，这样总有一些学生在作业里也用描点法。而且许多老师主张讲授完备性和纯粹性。我的方法是：

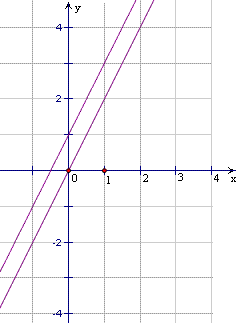
师：如图的直线上的任意一点(x,y)，x、y满足什么关系？

生：y=2x

师：对！这就是它的解析式。如果直线向上平移1个单位后x、y又满足什么关系？

生：y=2x+1

师：这是平移后的解析式。由此可见，直线的解析式都是一次函数，反之也然。

（3）勾股定理的引入

先让学生依次计算如图网格中绿色、蓝色、黄色正方形的面积。

绿色正方形面积= $(2+2)^2-4\times\frac{1}{2}\times2\times2$ ；

蓝色正方形面积= $(3+4)^2-4\times\frac{1}{2}\times3\times4$ ;

黄色正方形面积= $(1+3)^2-4\times\frac{1}{2}\times1\times3$ 。

如图设灰色直角三角形直角边分别为a、b，斜边为c，请学生利用上述计算方法推导出a、b、c的关系。

结果是： $c^2= (a+b)^2-4\times\frac{1}{2}\times{a}\times{b}$ 。

（4）轴对称图形与轴对称变换

剪“双喜”引入“轴对称图形”。纸张对折，中间放入复写纸，画一个图形后展开，由此引入“轴对称变换”。这两个概念的最大区别是，前者是一个图形，后者是两个图形。

2、教学方法因材而异

教学方法是教师和学生为了实现共同的教学目标和教学任务，在教学过程中运用的方式与手段的总称。它规定了教学参与者在教学任务中的角色、不同角色之间的相互关系以及每一角色的具体任务。教学方法有发现（探索）式、启发式、灌输式、自学指导法、尝试教学法、分层教学法、成功体验法等。教学模式，又称教学结构，是在一定的教育思想指导下建立的比较典型的、稳定的教学程序或框架。教学过程是分阶段的，在每个教学阶段都有其明确的教学目的和教学任务，因此需要采用不同的教学方法。教学过程的各个教学阶段是相互联系的，他们的排列顺序都有一定的逻辑性和科学性。教师在各教学阶段所采用的不同教学方法，也有着内在联系的，构成了一个严密的系统，这就是教学模式。

我们不谈深奥的理论，也不分什么“式”、什么“法”。到底是教学模式还是教学方法？干脆统称为“教学策略”吧。教学方法的运用要因学生、教材而异，不能说哪一种更好，优秀的教师就善于选择合理的教法，一堂课中会用多种教法。

如有理数加法法则、幂的运算法则、全等三角形判定等可以用发现式教学
勾股定理、相似三角形的判定等可以用启发式教学
三角函数、概率的意义、点的坐标等可以用灌输式教学

3、课堂练习多花时间

一节课中，新课、例题、练习时间之比通常为1∶1∶2，让绝大多数学生参与到学习中来，是教师的最重要的教学任务，参与的时间、形式、要求、实效是必须及时考虑的问题。学生课堂练习时，教师要及时发现学习问题，多展示学生问题比讲“怎么做”好得多。要关注学生的参与量，督促未及时参与的学生尽快进入角色。以个别练习为主，小组交流为辅。不要以为“合作交流”是“新理念”，是课堂教学的主流，不要作秀，不要流于形式。

4、解题方法思想领先

解题的策略要引导，数学思想要渗透、数学方法要多介绍。策略、思想、方法三者的关系如何？我认为数学思想指导下产生数学方法，而解题策略是数学思想和数学方法的统称。

关于数学思想和方法的关系，钟善基教授有过精辟的论述：数学思想是由知识转化为能力的结晶核。它将会把大量的有助于数学思想发展的素材吸附在它的周围，大大地加速概括的进程，并增强对材料的理解。因此可以把数学思想看成是一个对数学素材具强烈吸引力的“洞”。另一方面在数学思想的指导下，学生会积极开展新的探索活动，发现或创造出使用该思想的新例证、新方法，产生广泛的迁移。因此数学思想又可以看作一个“源”，大量的课题、方法和技巧，都可以从源中涌出。

初中阶段的学生，大多还处在模仿阶段，要求他们自己归纳出方法和思想是不切实际的。他们只有依靠教师的帮助，逐渐建立起数学思想，掌握数学方法，增加对数学策略的理解。下面举例说明。

在网格里画相似三角形要先计算还是先画图？这就是解题策略。一部分人是先画三角形，看看像不像；一部分人是先画三角形，再验证边长是否成比例；少数策略较好的人是先计算将已有的三角形边长乘以 $\sqrt{2}$ 、2、 $\sqrt{5}$ 、 $\sqrt{10}$ 等，这正是我们教师要引导的。
解决几何问题时要顺想思维还是逆向思维？这就是思考方法。有些几何题要顺着想，称为顺想思维，即从已知条件出发考虑问题的方法。有些几何题要倒着想，称为逆向思维，即从结论出发考虑如何解决。还有些要把两种方法结合起来运用。这个问题我会在专题文章里详述。
几何中求线段的取值范围要画图，可以用“极端原理”来解决，这就是解题方法。
5个数中选3个有几种选法要从反面考虑问题。
几何中的计数问题可以从数的规律入手，也可以从形的规律入手……，这既是策略也是方法。
平面直角坐标系中研究对称点的坐标，平移后像的坐标，平行线段的中点坐标等的坐标计算用画图的方法可以避免许多错误。如果一下子要学生记住规律和公式，恐怕一些学生会遇到困难。
有些问题还需考虑动手实验。另外还有列表、枚举、算式等都是我们常常选用的解题策略。
至于数学思想，以转化思想最为重要，要多渗透。

5、教师多讲未必好事

反对教师多讲，提倡少讲、精讲是人人皆知的理念，但能做到的教师不多。许多教师“好心”地给学生多讲一点，哪怕是学生在做题时也不放过，但收效甚少。我认为教师该讲的讲，该放的放，有些可以先讲后做，有些可以先做后讲，有些可以让学生看书自学，不要讲了。滔滔不绝的讲解很有可能引发学生的厌烦，好的同学他一讲就懂了；中等同学虽然讲了还不太理解，但多讲未必能记住；差的同学再讲也不懂。学生是做会的，而不是听会的。我曾经尝试着让学生自学课文，然后提几个问题就做练习，效果一点没有比教师讲授形式差，学生自学的科目有：

七上2.8《计算器的使用》
七上3.3《立方根》、3.4《用计算器进行数的开方》
七上4.3《代数式的值》
七上6.4《扇形统计图》
八上1.4《平行线之间的距离》
八上2.1《等腰三角形》
八上3.1《认识直棱柱》
八上6.3《坐标平面内的图形变换》
八下4.2《证明》
八下5.2《平行四边形》
九上3.1《圆》
九上4.4《相似三角形的性质及其应用2》
九下1.2《有关三角函数的计算2》
九下1.3《解直角三角形3》
九下2.3《概率的简单应用》

6、看书预习不利教学

有许多老师要求学生回家复习和预习，我个人认为复习要的，预习就要分析一下利弊得失了。有些课带有探索性和研究性，教师要设置一些悬念，如果学生预习了课文的内容，探索、研究、悬念就无从入手了。而且有些课为了需要，上课时不让学生翻阅课本。对于老师的提问，有些学生习惯于从书里找答案，他们懒于思考，不善分析，这对培养学习能力是不利的。

7、听懂会做两码事情

我常常纳闷，为什么我讲得这样生动，学生听得如此专心，作业也会做了，都听明白了，可是考试就是不行。究其原因是作业不是独立完成，概念没有真正理解，方法没有牢固掌握。

下面摘录一位科学老师对“听懂而不会做”的现象分析，相当精辟。

日常教学中，常听到一些老师抱怨：“我已经告诉他多少遍了，可是他就是听不进去，一错再错，真是不可救药 ”在一次又一次地“告诉”不见效果后，有的老师干脆放弃了对“这些一错再错的学生”的辅导与帮助。

也有老师这样说：“每次上完课后，我都要问这些学生听懂没有，他们都说听懂了。可是一做练习题，他们就束手无策。哎，我真没办法教他们了。” 看看说这些话的老师，个个都辛苦得很。教初三毕业班的责任重，压力大呀！他们整天在忙着批改作业，忙着精心备课，忙着如何把知识讲清楚，忙着精选习题出考卷，忙得不可开交。

说这些老师不负责，真是冤枉他们。既然如此，为什么还会有“听懂而不会做”，“说了一遍又一遍，仍然一错再错”的现象出现呢？

其实，这些老师给学生的是知识的精华───“高营养”的知识。然而，学生没有吸收这些营养的“根”───学习的能力。因此，教师就必须在促使学生“根”的发育与生长上做文章，即在培养学生的学习能力上作研究。

我们是否可以反思一下自己的教学，反思一下自己的课堂教学的方法，想一想在教学过程中学生是否有进行独立思考的时间与机会？教师是否在学习方法给予学生切实的指导？在现实中，一些老师乐于把知识灌输给学生，一切问题都先帮学生解决，不用学生动脑思考。他们习惯于让学生把板书记下来，然后叫学生去死记硬背！这好比是植物进行光合作用一样，有了二氧化碳和水这些原料（就当是老师上课讲的知识），有了叶绿体（就比作是学生的大脑），可是，没有光（反应的条件───比作是学习的能力与学习方法），光合作用也是反应不起来啊！怎样来培育学生的学习能力？关键在于老师是否给学生“光”，也就是给学生学习的方法，培养其学习能力。

8、螺旋上升反复记忆

既然学生的理解、记忆符合一定规律，我们教师就要给足理解、记忆的时间，要反复，要螺旋上升，要时常帮学生回忆知识。学几何时做做代数，学代数时做做几何，学二次函数时做做一次函数。

一位学生在论坛里请教数学问题：我觉得有些压轴题在课上听懂了，过几天重新做又不会了，老师说是练少了，但是我觉得每天完成了那么多作业之后也就没有时间来看这些题了，而且准备个错题本也很不实际，因为完成那么多作业还来不及呢！请教大侠有什么好方法？

一位大侠回复道：我以前上学的时候也有这种感觉，现在想想，感觉是因为自己本来没做过这些题，老师讲了他的解题思路，当时听懂了，可是那个思路自己总是不经常想到或者就不会那么想这个问题，我觉得还是因为基础知识不扎实吧。还有就是大脑每天接受到的信息量太多，遗忘很多信息也是自然，常常是学过的东西就忘了或者过段时间不看就忘了，不是有个记忆曲线吗，所以我建议老师讲完的题你可以当天晚上抽出5分钟时间（5分钟总是有的吧，上厕所看也行）看一遍，回忆一下解题思路，然后隔两三天再看一遍，一周后再看一遍，应该就记住拉。