关于sinα+cosα最大值的解答征集

为了提高本博客的互动性，我在上篇文章《征求解答》中提出了一个初中数学问题：

如果 $\alpha$ 为锐角，那么 $sin{\alpha}+cos{\alpha}$ 的最大值为 $\sqrt{2}$ 。

请你将证明过程在下面评论里给出，证明的依据不能超过初中知识。

本问题的结论是我很早时候自己发现的，我想一定会引起更多老师的兴趣。结果征集到五位老师的四种解答（有些解答在QQ中交流），公布如下。

解法一：

设直角三角形锐角 $\alpha$ 的对边、邻边和斜边分别是a、b、c，则有

$sin{\alpha}=\frac{a}{c}$ ， $cos{\alpha}=\frac{b}{c}$ ，

(sin{\alpha}+cos{\alpha})^2=(\frac{a+b}{c})^2=1+\frac{2ab}{a^2+b^2}=1+\frac{2}{(\sqrt{\frac{b}{a}}-\sqrt{\frac{a}{b}})^2+2}

当a=b时，

原式的最大值=1+1=2，所以 $sin{\alpha}+cos{\alpha}$ 的最大值是 $\sqrt{2}$ 。

设直角三角形锐角 $\alpha$ 的对边、邻边和斜边分别是a、b、c，则有

$sin{\alpha}=\frac{a}{c}$ ， $cos{\alpha}=\frac{b}{c}$ ，

$(sin{\alpha}+cos{\alpha})^2=(sin{\alpha})^2+(cos{\alpha})^2+2sin{\alpha}cos{\alpha}=1+\frac{2ab}{a^2+b^2}$ ,

因为 $a^2+b^2\geq2ab$ ,

所以，原式 $\leq{1+1=2}$ ,

因为 $sin{\alpha}+cos{\alpha}\geq0$ ，

所以 $sin{\alpha}+cos{\alpha}\leq\sqrt{2}$ 。

如图，在单位圆里画任意的内接△ABC，使AB为直径。

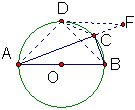
$sin{\alpha}+cos{\alpha}=sinA+sinB=\frac{AC+BC}{AB}$ ，取上半圆的中点D，我们可以证明AC+BC≤AD+BD。

在AC延长线上取CF=CB，∵∠DCB=180°-∠DAB=135°，

∠DCF=180°-∠DCA=135°，∴∠DCB=∠DCF，∴△DBC≌△DFC，∴DF=DB，

∵AD+DF≤AF，∴AC+BC≤AD+BD。

于是 $sinA+sinB=\frac{AC+BC}{AB}$ ≤ $\frac{AD+BD}{AB}$ = $\sqrt{2}$ .

用高中两角和公式推导，虽然不符合要求，但确实是一个最简单的方法。

$sin{\alpha}+cos{\alpha}=\sqrt{2}(\frac{\sqrt{2}}{2}sin{\alpha}+\frac{\sqrt{2}}{2}cos{\alpha})=\sqrt{2}sin(45^{\circ}+\alpha)$ ，

可见，当 $\alpha=45^{\circ}$ 时， $sin{\alpha}+cos{\alpha}$ 的最大值是 $\sqrt{2}$ 。

老师们，当我编出新的数学题时，我们再来一次如何？是否喜欢这种互动形式呢？请在评论里发表你的看法。谢谢。

今又收到一位学生（2011届徐铿）的解答：

设 $sin\alpha=x$ ，因为 $sin^2\alpha+cos^2\alpha=1$ ，所以 $cos\alpha=\sqrt{1-x^2}$ ，

要证明 $sin\alpha+cos\alpha\leq\sqrt{2}$ ，

只要证明 $x+\sqrt{1-x^2}\leq\sqrt{2}$ ，

即 $\sqrt{1-x^2}\leq\sqrt{2}-x$ ，

两边平方后并变形得 $(\sqrt{2}x-1)^2\geq0$ ，这显然成立。

（2010年12月19更新）