学生的信
黄老师好,我是十九中15届2班的仵少辉,是您曾经的学生。因为春节将至,也早已打算给老师你在春节前说些话,所以在这个时候用这种方式完成我这个打算已久的准备。
老师你可能很好奇为什么我通过这种方式,来给你说我的这些话。那就听我慢慢解释吧。
去年中考结束后,因为成绩的原因不得不回老家读书了。那时候心里难过至极,觉得自己什么都没有似的。就这样从七月份开始,离开了自己生活了九年的宁波。那整个暑假一直生活在乡下的舅舅家。那段时间,自己的心逐渐平和,开始能体会一些这世间的真诚的不虚假的道理。每晚都望着星星,一步步的与自己交流。而我感动的是母亲一直在为了我的学业问题四处奔波。好的消息是九月份我进了市第二的一所高中(因为留有几个外地转回生的名额)。我曾经在初中和同学说过,初中我被压抑的所有,要在高中全释放出来。虽然中考失利,让我迷茫过,但我认为那是我青春的一站充满雨雾的风景,而我用微笑的表情去面对它,便觉得也是一种美。
在高中的一切总的来说还算不错,更多的是心里充满了一股劲。也担任了文学社的副社长、器乐社吉他组的组长和下学期辩论赛的总负责人。当然在高中有乐也有苦,高一的科目与功课多了,对思维的要求高了,每晚的休息时间少了,自己钻研的时间也少了。或许是对高中科目找到了比初中更加好的习惯和态度,自己的兴趣也越来越高。最终期末考试的全校名次定格在67/800(数学单科21/800)。的确是这学期最好的一次,很开心。但我依旧想朝着远方的道路走。做好自己。
本想写封信给老师,但由于不知道老师现在在那里教学,并且因为我要准备期末考,很难抽出时间去写,所以打算放到寒假写,但怕寄到的时候我父亲找不到你(我与母亲回老家了,父亲依旧留在宁波工作),就只好用这样的方式了。
说实话,黄老师你其实是对我影响最深的一位老师。现在回想起初中关于老师你的故事,都会觉得很幸运很美妙。记得你是初二开始教我们的,两年发生了太多,我还记得你说从圆规的使用就可以看一个人的数学水平,你说圆规的铅笔头要磨扁平,这个习惯我一直用着,并且觉得很好。我记得你教我们教室地面上的污垢要用鞋底摩擦才好弄干净。记得你当堂在投影幕布后垫一本书,银幕就能放下;记得你罚我去你办公室倒垃圾的那次;记得你刚教我们时推荐的“传送门”这款游戏;记得你介绍你的博客――“你不会忘记”;记得你鲜活的课。你说的习惯决定一切和要从反面考虑问题我一直记在心里。记得曾经一段时间每天晚上钻在被窝里翻着你的博客;记得初三下学期每晚《甬真集》作到十一、十二点;记得那次自己用几何画板发现了新东西兴奋的睡不着觉,白天又兴冲冲的去找你的心情。如今你的博客依旧在我的收藏夹中,那两本《甬真集》依旧还留着,它是属于我青春的回忆。对于你在我心中片段有很多很多。是你让我对数学有了极大的兴趣和自信;是你让我懂得站在更高的角度看待问题;是你让我体会到面对生活的态度。你对我的影响有很多,对你的话语我永远记在心中。
如今我在陕西宝鸡继续我的学业,您在甬城继续你的教学期望。大年在即,祝愿老师身体安康,老当益壮。祝愿老师的殷切希望终会实现。望老师全家幸福,明天吃一顿完美的年夜饭。
您是我永远绽放的烟花,我坚信我们一定会再见面的。
你的学生――仵少辉
2016年2月6日
我的点评:
这封信最终是通过QQ传给我的。
仵少辉,初二接班时是一个内向、腼腆的男孩,数学成绩很一般。与众不同的是他不抄作业,愿意自己钻研。这年头,不抄作业是一件新鲜事儿。
没想到他会将我的话记得这么牢,把我传授的方法用得这么好,在高中担任了众多职务,看来他的各方面的能力优于一般人,真的在初中没有显露。
记得初三下学期,他研究数学的劲头十足,常有新的问题产生,跑到办公室和我分享成功的次数就达3次。下图是2015年6月5日他给我看的草稿,内容是推导任意三角形内心与外心的距离公式。
2015年4月13日他那着几何画板文件(他几何画板玩的很好),给我看的问题是:
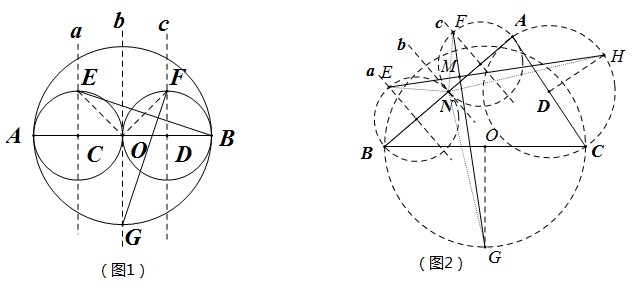
问题1 如图1,已知AB是圆O的直径,直线a,b,c垂直且四等分AB,以AO,BO为直径的圆交直线a,c于E,F,直线b交圆O于G,求证:EB与FG垂直且相等。
问题2 已知△ABC中,BC是圆O的直径,直线a,b,c垂直且四等分AB,以AN,BN为直径的圆交直线a,c于E,F,BC的中垂线交圆O于G,AC的中垂线交以AC为直径的圆于H,求证:EH与FG垂直且相等.
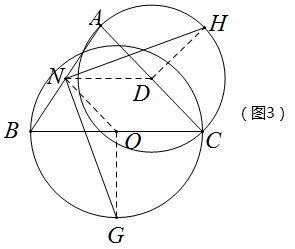
他自己备注说:问题2的关键就是求证NG与NH垂直且相等,如图3.
2015年5月12日他又兴冲冲跑到办公室分享了研究成果.
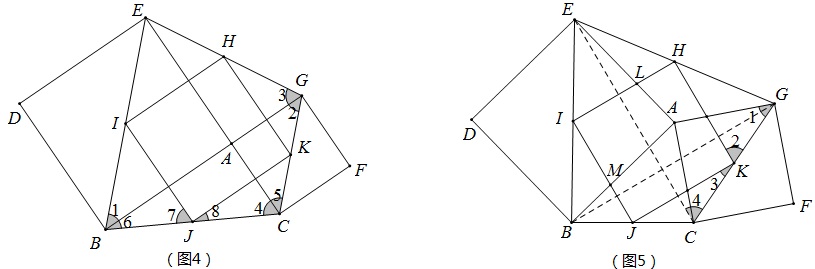
问题3 如图4,已知:RT△ABC,分别以AB、AC为边向三角形外作正方形ABDE、正方形ACFG,连结EB、EG、GC并取其中点I、H、K,取BC中点J,连结 IH、HK、KJ、JI。求证:四边形IHKJ是正方形.
问题3证明:
∵RT△ABC、正方形ABDE、正方形ACFG,
∴∠1=∠2=∠5 、AE=AB、AG=AC ∠EAB=∠BAC=∠CAG=90°,
∴EB∥GC、∠EAG=360°-4×90°=90°,
∴梯形EBCG、∠BAC=∠EAG,
∴△ABC≅△AEG(SAS),
∴∠3=∠4,∴∠2+∠3=∠4+∠5,即∠EGC=∠BCG,∴等腰梯形EBCG,
∴BG=EC,∵I、H、K、J为中点 ,∴菱形IHKJ,∴BG∥JK、EC∥IJ,
∴∠6=∠8、∠4=∠7,∵∠6+∠4=90°,∴∠7+∠8=90°,
∴∠IJK=90°,∴正方形IHKJ.
问题4 如图5, 对于任意△ABC,其他条件如问题4,求证:四边形IHJK是正方形.
问题4的证明:
证明:连结BG、EC,
∵正方形ABDE、正方形ACFG,∴∠EAB=∠GAC=90°、AE=AB、AG=AC,
∴∠EAB+∠BAC=∠GAC+∠BAC,即∠EAC=∠GAB,
∴△EAC≅△BAG(SAS),∴BG=EC、∠AGB=∠ACE,
∵IHKJ为中点,∴菱形IHKJ ,∴BG∥JK、EC∥HK,∴∠1=∠3、∠ECG=∠2,
∵ ∠4+∠1+∠AGB=90°,∴∠4+∠1+∠ACE=90°,即∠1+∠ECG=90°,
∴∠3+∠2=90°,∴∠HKJ=90°,∴正方形IHKJ.
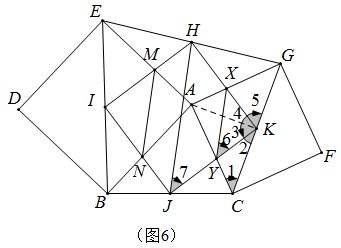
问题5 如图6,其他条件如问题4,连结MN、HJ、XY,证:IM=IN、MH=NJ、HX=JY、XK=YK.
问题5的证明:
连结AK,∵等腰RT△AGC、K为中点,∴AK=CK 、∠CAK=∠GAK、∠2+∠3=90°,
∴∠CAK=∠1,∴∠GAK=∠1,∵等腰RT△JHK,
∴∠3+∠4=90°,∴∠2=∠4,∴△CKY≅△AKX(ASA),∴YK=XK,
∴等腰RT△XYK,∴∠6=45°,∵∠7=45°,∴∠6=∠7,
∴HJ∥XY,∴HX/JY=XK/YK,∴HX=JY
同理:IM=IN、MH=NJ.
最后一次让我看的问题有点超过了初中的要求。
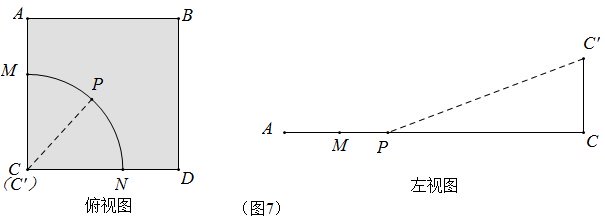
问题6 如图7,一片边长为40km的正方形海域,在点C处有一座高为20m的灯塔,为使灯塔所能照射到的的面积是海域的一半,那么光线的长度范围为多少?
仵少辉自解:可以根据左视图的提示,求出CP最大值的长,再用勾股定理求出C’P,其长度范围也为0∼C’P最大值。
由已知 ,
, ,
,
 ,
,
C’P最大值= .
.
点评:点光源的光线方向是四射的,最短的光线长是左视图中的CC’=20m,最大的是俯视图中的CP,所以四射的光长有个取值范围.
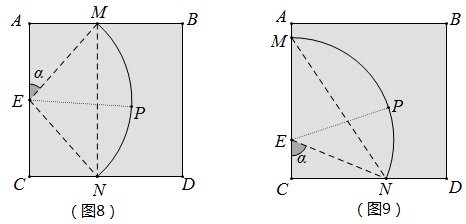
问题7 如图8,其他条件不变,当灯塔E在AC中点E时,求光线的长度最大值多少?
仵少辉自解:问题的关键在于俯视图中的圆弧半径,所以在此只求EP(r)。
 ,
, ,
, ,
,
 .
.
点评:解这个关于r的方程有点麻烦.
问题8 如图9, 其他条件不变,当灯塔E在AC四等分点时,求光线的长度最大值多少.
仵少辉自解:
 ,
, ,
, ,
,
 .
.
仵少辉自评:
根据判断两方程的解不同,说明当所照海域位置变化时,要使灯塔所照面积为海域面积一半时,其光线的长度范围是变化的,那么如何使其为定量?
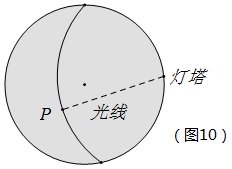
问题9 如图10,发现当海域为圆形时,光线的长度范围不随所照海域的位置改变而改变,若海域半径为20km,那么光线的长度最大值为多少?
一个初中学生研究数学能到如此地步,是我从教以来第一人,更难能可贵的是几何画板玩得比数学老师都好。我珍惜这样的人才,也希望仵少辉在高中继续研究。分数高低不能评判一个人的能力,事实说明兴趣是第一老师,也许正因为这样的兴趣,使一个人最终走向成功,我期待着。


老师,学生都让人动容。
老师是孩子人生的领路人!
今天一翻开看到这篇博客,觉得老师之于学生真的很重要,一辈子能碰到你这样的好老师是学生的幸运!我以江东有你这样的老师为荣!
黄老师的修养和为人成就了这个孩子,成绩并不代表一切,能力才是关键。能钻研能思考能提问能悟道的孩子肯定会有一番大作为,说不定是下一个黄sir,哈哈