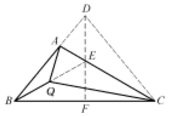
如果三角形的三个角的度数都是10的整数倍,三角形内一点与三角形的三个顶点分别连结后,得到的所有的角也都是10的倍数,我们称这样的点为三角形中的格点.求解三角形中的格点问题,常可利用对称点.利用对称点求解三角形中的格点问题,方法简单易行,解法简洁巧妙,题面新颖有趣,是学生巩固知识,培养能力,陶冶情操,提高素质的宝贵资料.
证明角格点的方法是作轴对称图形,即构造轴对称的全等三角形。
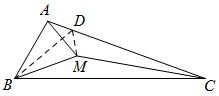
例1 在△ABC中,∠ABC=60°,∠ACB=20°,M为∠ACB的平分线上一点,∠MBC=20°.求∠MAB的度数.
解:如图,设∠MBA的平分线交AC于D,连DM.显然,BM平分∠DBC,而CM平分∠DCB,即M为△DBC的内心.可知∠MDB=∠MDC=60°.有∠ADB=60°=∠MDB.故点A与点M关于BD对称.则∠MAB=90°-∠DBA=70°.
这里证得“点A与点M关于BD对称”是问题的关键。
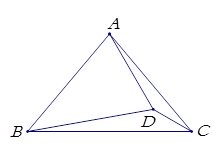
例2 如图, 已知△ABC中,AB=AC,∠BAC=80,点D是△ABC内一点,且∠CBD=10°,∠ADC=20°,求∠ADB的度数.
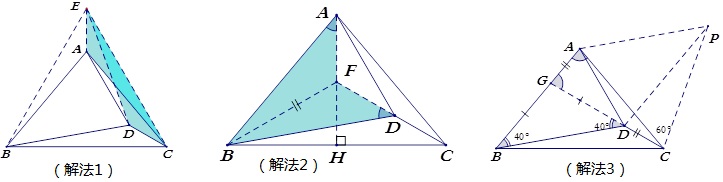
解法1:把△BDC沿直线CD作轴对称变换至△EDC.则∠ECB=2∠BCD=60°,EC=BC,∴△BCE是正三角形,又∵ AB=AC,∴直线AE是△EBC、△ABC的对称轴,∴∠AEC=∠AEB=30°=∠ECD,∴易证△AEC≌△DCE,即四边形ADCE为等腰梯形,∴∠ADC=150°,又∠BDC=140°,∴∠ADB=70°.
解法2:作BC边的高AH,延长CD交AH于点F,连结BF.∵ AB=AC,∴AH是△ABC的对称轴,∴FB=FC,∵∠BCF=30°=∠FBC,∴∠BFD=120°=∠BFA,∠BDF=40°=∠BAF,BF=BF,∴△AFB≌△DFB,∴FA=FD,∠ADF=30°,∴∠ADB=70°.
解法3:延长CD交AB于G.由题知∠CGA=∠CAG=80°,∠GBD=∠GDB=40°,∴CG=CA=AB,GD=GB,∴CD=AG,以CD为底边构造等腰△PCD,使PC=PD=AC,且P、A在直线CD同侧,∴∠PCD=∠PDC=80°,∠CPD=∠ACG=20°,∴∠PCA=60°,△PAC是等边三角形,∠APD=40°,∠PDA=70°,∴∠ADC=150°,∠ADP=70°=∠ADB.
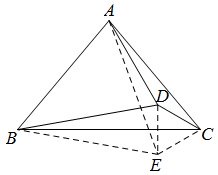
解法4:如图,作正三角形ABE连结EC,ED,易证BD=BE=AB,故∠ADB=(180-40)÷2=70°。
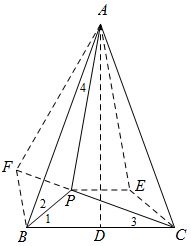
例3 如图,△ABC中,AB=AC,点P是三角形内一点,∠1=40°,∠2=30°,∠3=20°,
(1)求∠4的度数;
(2)求证:AP=BP+CP。
解:(1)作高AD,作点P关于AD的轴对称点E,作点P关于AB轴对称点F,易证PE=CE=PB,△PBF为正三角形,F,P,C共线,△AFP≌△APE,∴以A为顶点的每个最小的角都为10°,即∠4=10°;
(2)显然∠FAC=∠FCA=50°,AP=FA=FC=FP+CP=BP+CP.
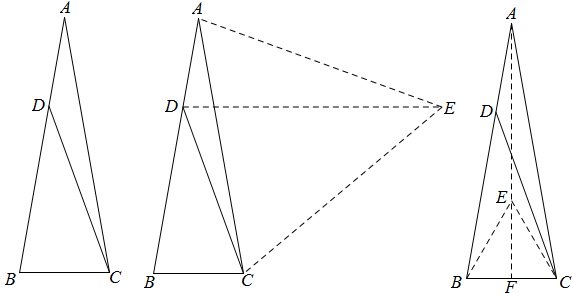
例4 如图,AB=AC,∠A=20°,点D在AB上,AD=BC,求∠BDC的度数。
解法1:作正三角形ACE,连DE,这样△ADE≌△ABC,于是△ADE和△DCE均为等腰三角形,且顶角为20°和40°,于是不难求出∠BDC=30°.
解法2:作正三角形BCE,不难证明△CEA≌△ADC,于是不难求出∠BDC=30°.
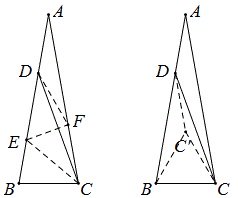
解法3:作△ABC的角平分线CE,在AC上取点F使CF=CB,在AB上取点D’使D’F=FC,不难证明AD’=BC=AD,即D’与D重合,从而可以计算∠BDC=30°.
解法4:作正三角形BCC’,连DC’,不难证明四边形ADC’C是等腰梯形,所以C’D=C’B=C’C,即C’是△DBC的外心,所以∠BDC=∠BC’C÷2=30°.
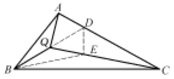
例5 在△ABC中,∠ABC=50°,∠ACB=30°,Q为形内一点,∠QBA=∠QCA=20°.求∠QAB的度数.
解:如图,设BQ交AC于D,过点D作BC的垂线交QC于E.连BE.
由∠QBC=30°=∠ACB,可知DE为BC的中垂线.由∠QCB=10°,可知∠EBC=10°,∠QBE=20°=∠QBA.
由∠EDB=60°=∠EDC,可知∠BDA=60°=∠BDE.有点A与点E关于BD对称. 则∠QAB=∠QEB =∠EBC+∠ECB=20°.
这里注意到BQ是∠AQC的平分线,故想到在QC上取点E,使∠EQB=∠ABQ,则点E为点A关于BQ的对称点.为此想到满足条件的点E,恰为BC中垂线与QC的交点。又由∠QBC=30°=∠ACB,想到BQ与AC的交点D应为BC中垂线上的另一点.于是,我们选择了如上的方法找到点A关于BQ的对称点E.
例6 在△ABC中,∠ABC=50°,∠ACB=30°,Q为形内一点,∠QCA=∠QAB=20°.求∠QBC的度数.
解:如图,设BC的中垂线分别交BA、AC于D、E,F为垂足.连QE、BE、DC.
由∠ACD=20°=∠ACQ,∠DAC=80°=∠QAC,可知点D与点Q关于AC对称.有 ∠AEQ=∠AED=∠FEC=60°.
由∠BEF=∠FEC=60°,可知∠AEB=60°=∠AEQ.有B、Q、E三点共线. 则∠QBC=∠EBC=30°.
这里注意到AC是△AQB的∠QAB的外角平分线(这一点并不引人注目),在BA延长线上取一点D,使DA=QA,则点D为点Q关于AC的对称点.为此我们通过BC的中垂线,把∠ABC“翻折”到∠DCB的位置,是非常恰当的.
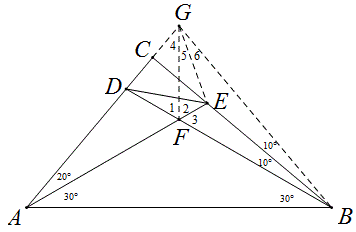
例7 如图△ABC中,∠C=90°,D,E分别在AC,BC上,∠CAE=20°,∠EAB=30°,∠CBD=10°,求∠DEA的度数。
解:沿BC反射△BCD,得到△BCG,连结GE,GF,
易证GF平分∠AGB,∴∠1=∠2=∠3=60°,∠4=2∠5=2∠6=40°,
则E为△BFG的内心,∴△DEG为正三角形,
∴∠CED=30°,∵∠CEA=70°,∴∠DEA=40°。