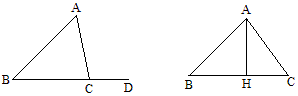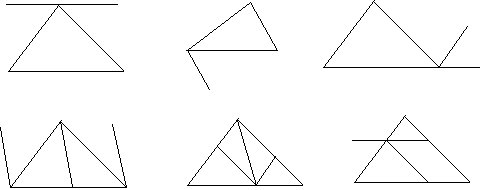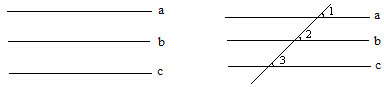在初二下《命题与证明》中,有证明“三角形内角和等于180°”的学习内容。
上课一开始,我说:这个定理我们早在初一甚至小学就用了,就是没有证明,最多只是用实验的方法加以验证。今天请大家证明一下。
学生的证明方法有:
方法1:延长BC至D,∵∠ACD=∠A+∠B,∠ACD+∠ACB=180°,∴∠A+∠B+∠ACB=180°.
方法2:作高AH,∴∠BAH+∠B=90°,∠CAH+∠C=90°,那么∠A+∠BAC+∠C=180°.
见了学生的解法,我说:老师也提供一种证法。
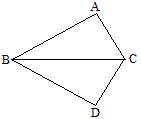
方法3:如图,反射△ABC得△ABD,∵四边形ABDC的内角和为360°,故∠A+∠ABC+∠ACB=180°.
我问:这个方法好吗?学生齐答:好!
我因势利导,问:你们知道以上三种方法的证明中用到的依据是什么?学生答:
三角形的一个外角等于和它不相邻的两个内角的和.
直角三角形的两个锐角互余.
四边形的内角和等于360°.
再问:这三个定理是靠什么证明的?学生:这…….想不起来了.
我告诉学生:这三个定理无一例外地都是用三角形内角和定理证明的,你们知道这有什么不妥吗?学生摇摇头.
我举了一个例子,假如有一种字典,解释“清”的含义说:“洁也,请见第×页”,翻到“洁”后解释是:“清也,见第×页”.大家纷纷说:这算什么字典,它等于什么也没解释.
我说:对啊,那我们用三角形内角和定理证明三角形外角定理,又用三角形外角定理证明三角形内角和定理,这不也是什么都没证吗?
这下学生明白了,上面的三种方法都是错误的.我明确地告诉学生:“这叫循环论证”.
接下来学生的证明方法五花八门,所用的方法无一不是用平行线的.(见下图)
过了2天,课题是《4.4 反证法》,要证明的定理有2个:
定理1:在同一平面内,如果一条直线和两条平行线中的一条相交,那么和另一条也相交.
定理2:在同一平面内,如果两条直线都和第三条直线平行,那么着两条直线也互相平行.
书上是用一个公理“经过直线外一点,有且只有一条直线平行于已知直线”来证明定理1的.
我用如下方法.
已知:a∥b,c与b交于P,求证:c与a也相交.
证明:假如c∥a,∵a∥b,∴c∥b,这与“c与b交于P”矛盾,∴c与a也相交.
接下来我请大家证明定理2,学生的方法有2种.
已知:a∥b,c∥b,求证:c∥a.
方法1:假设c与a相交.∵a∥b,∴c与b相交,这与“c∥b”矛盾,∴c∥a.
方法2:作第4条直线与a,b,c都相交,∵a∥b,c∥b,∴∠1=∠2,∠2=∠3,
∴∠1=∠3,∴c∥a.
证完后我问:当这2个定理的如上证明方法出现在同一块黑板上,你们认为有什么问题吗?
学生没发现问题,再问:定理1的证明中用到了什么?定理2的证明方法1中又用到了什么?这下学生有反应了:哇!是循环论证.
那么方法2可以吗?齐答:可以.
其实方法2中的辅助线是第4条直线与a相交,那么为什么也会和b相交呢?这是定理1的缘故,所以依然是循环论证.
最后师生达成一个共识,这2个定理的证明至少有一个要用公理来证.