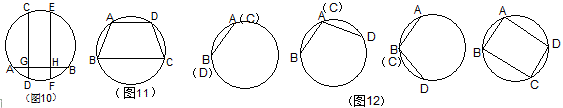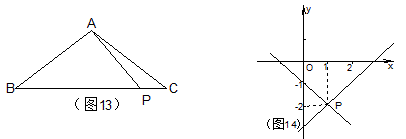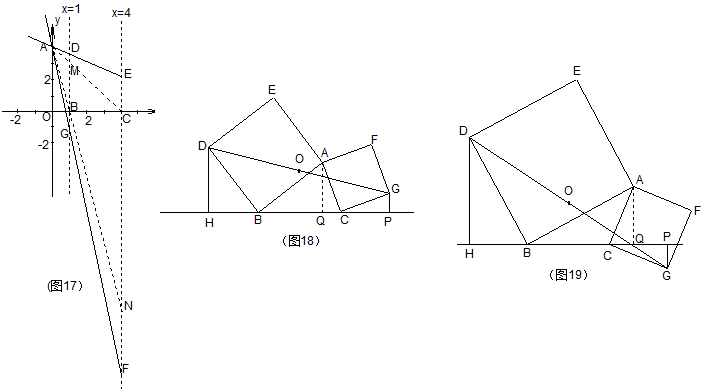万物都是运动的,自然界的许多客观规律是通过运动方式显示出来的,运动使世界变得丰富多彩。小至电子电荷,大至宇宙空间,所有运动的物体无一不可以看作点线面体的几何元素,所有的运动无一不可以看作几何图形的位置变化。所以用运动思想研究几何图形,用运动的方法讨论数学问题,是我们数学教学的重要任务。
然而使我们担忧的是现在的很多学生缺乏运动思想,在他们看来画在纸上的图形都是“死”的,都是一成不变的,解决问题时根本没想到对某些元素进行运动变化,结果图形之间的内在联系发现不了,一些变化规律无法显示出来,于是问题就难以得到解决。
一次在初三总复习中有这样一道练习题:
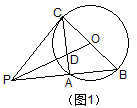
例1 如图1,⊙O的半径为1,P在⊙O外,PO=\sqrt{5},PAB为割线,BC为直径,设PA=x,PB=y。(1)求y关于x的函数解析式,并求自变量x的取值范围。(2)当PA=AB时求CD的长。
很多学生不会求自变量的取值范围,他们不知如何列出不等式(学生们习惯于列不等式求自变量的取值范围),于是无从下手。
事实上将BC看作定圆O中的定直径,而P是动点。因PO=\sqrt{5},故P只能在以O为圆心、\sqrt{5}为半径的圆上运动,割线PAB的位置随着P点的移动而变化。当PAB为切线时PA=2,所以x<2。当PAB通过圆心O时PA=\sqrt{5}-1,所以x≥\sqrt{5}-1。
于是x的取值范围是\sqrt{5}-1≤x<2。
当我把这个运用运动思想解决问题的方法介绍给学生后,学生们对这种思想方法很感兴趣。但我却忧心忡忡,这种思想平时教学中灌输得不少,为何学生总是想不到呢?后来分析其原因有这么几点:
1、缺乏运动观念,难以形成运动思想
改变这种状况的关键是让学生比较系统地接受这方面的训练,在初三总复习时这种训练是可行的。让学生比较用运动方法解题与列不等式解题的优劣,从而更新思维方式,更新数学观念,强化数学思想。
2、虽有运动思想,但难以确定动元素和定元素
这实际上与审题大有关系。教师平时教学中多强调动元素与定元素是很有帮助的。如上例中我们还可以将P看成定圆O外的一定点,而直径BC看成是动线段,问题也可以得到解决。
3、运动时元素间的关系难以想象
这是缺乏空间想象能力的表现。要将画在纸上的“死” 图“活”起来,要有较强的想象能力。锻炼这种能力的方法有两种,其一利用几何画板软件制作成多媒体课件。如上例中的图形若放在几何画板中,则运动自如,PA的长度变化规律显而易见。经常让学生观察“活”的图形,能使他们面对“死”的图形展开想象的翅膀。其二是建模,这里的“建模”与通常说的建模思想中的“建模”不同。如上例中可以想象有这么一个模型:用铁丝做成的⊙O中有一条固定的直径BC(BO=1),用长\sqrt{5}的铁丝做成PO(能绕O转动),PC、PB是用橡皮筋做的,当转动PO时,想象PB与⊙O的交点A与P的距离的变化情况。这种把几何问题想象成一个实物模型的过程便是建模。
下面通过分类讲述来谈谈运动思想是怎样帮助我们解决数学问题的,我们应该如何在教学中渗透这种思想。
一、定值探求
不少数学问题是在诸多变量存在情况下,探求定值或求定值的大小。我们可以运动其中的动点到不同的位置,观察其变化情况,也可以运动至最特殊的位置来求定值的大小。
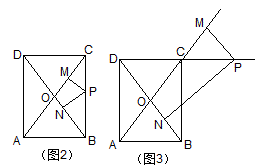
例2 如图2,矩形ABCD中,AB=15,BC=20,表示点P到AC、BD的距离的线段是PM、PN。(1)若P在BC上移动,则PM+PN的大小是否改变?(2)若P在矩形边界上移动时PM+PN的大小也不变吗?(3)若P在DC的延长线移动,PM+PN还不变吗?
分析:(1)将P点移动至C、B及BC的中点,发现PM+PN都等于C到BD的距离12。于是我们有理由猜想PM+PN是定值,且这个定值等于12。
(2)仿(1)。
(3)当P在DC延长线移动越来越远离C点时,PM与PN都越来越大(如图3),故回答是否定的。如果更深入研究可发现,PN–PM是定值。
二、最值问题
许多最值问题往往可以用二次函数来解决。但如果考虑运动思想,可以收到事半功倍的效果。
例3 如图4,Rt△ABC中,∠C=Rt∠,AC=8,BC=6,D在AB上,DE⊥AC于E,DF⊥BC于F。问矩形DECF的面积是否有最大值或最小值?如果有的话,D在何处?面积为多少?
分析:设想D在AB上由A点开始向B点移动(A、B两点虽不能到达,但暂且当作极端点),矩形的面积随之由0逐渐变大,以后又逐渐变小,最后又变为0。我们不难猜想矩形的面积是某一变量的二次函数(在初中阶段只有二次函数才具有这样性质),而且有最大值,根据二次函数图象的对称性,当D在AB中点时面积最大。因为此时DE、DF为中位线,故最大面积为12。
例4 如图5,正方形ABCD中AD=2,E在AD上,F在AB上,G在DC上,且AF=ED,DG=AE,问五边形EFBCG的面积是否有最大值或最小值?如果有的话,此时E在AD何处?面积是多少?
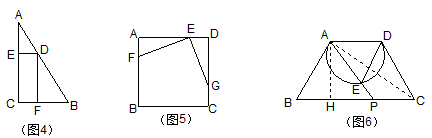
分析:仿照上例,让E自A向D移动,发现五边形的面积从大变小,再由小变大。可估计当E在AD中点时面积最小,最小面积为2×2-1×1÷2×2=3。
三、取值范围
由于一点运动而产生许多变量,其中得到的函数问题称为动点函数(如例1)。这类问题中求自变量取值范围时,许多学生常用不等式来解决。其实运动思想是解决这类问题的首选思想。
例5 如图6,等腰梯形ABCD中,∠B=∠C=60°,AD=6,AB=10,优弧AD与两腰分别切于A、D,P在BC上,AP=x,DE=y。
(1)求y关于x的函数关系式;(2)求x的取值范围;
(3)求y的最大值。
分析:(1)可由⊿ABP∽⊿DEA,得y=\frac{60}{x}。
(2)将P点由B点运动至C点,把AP想象成橡皮筋(梯形及弧用铁丝做成),运动时可发现AP与AH重合时橡皮筋最松(AP最小);AP与AC重合时橡皮筋最紧(AP最大)。而经验不足的学生会说AP与AB重合时最小。
∴AH≤x≤AC,经计算AH=5\sqrt{3},AC=14,∴5\sqrt{3}≤X≤14。
(3)当AP⊥AD时DE为直径,圆中的弦以直径为最大,
故当x=5\sqrt{3}时,y最大值=\frac{60}{5\sqrt{3}}=4\sqrt{3}。
如果将(3)的问题改为求弧所在的圆的直径的话,可能做得出的学生就更少了。
四、动点轨迹
求点的轨迹(运动时留下的痕迹)常有两种方法。一种是发现动点满足的条件,并判断这个条件符合哪个轨迹定理,从而求得点的轨迹。另一种是在很难判断符合哪个轨迹定理的情况下,将动点按题设条件进行运动,然后观察其形成的轨迹进行猜想(当然最后还得证明)。
例6 已知△ABC,一动圆O与AB、AC都相切,且⊙O上各点都不在△ABC外,则点O的轨迹(运动时留下的痕迹)是___________。
我测试过许多学生,对解决本题都感到困难。但有运动思想的学生会通过对动圆的运动(如图7),不难判断点O的轨迹是△ABC的内心与点A的连线(A点除外)。
我们说现在的学生缺乏创新思维的理由就在这里。他们会做熟悉的题,但不会做陌生的题。所以我们培养学生的运动思想,实际上就是培养他们的创新能力,使他们掌握更多的分析问题和解决问题的方法,从题海中跳出来。
五、判断错误
不少选择题用排除法来解会显得简捷。但要排除错误才能选择正确的答案。有不少学生得出了错误结论自己浑然不知,这是因为缺乏判断错误的能力。用动态方法来判断错误是一种较为精妙的方法。
例7 如图8,用半径为r的两根钢棒嵌在大型工件的两侧,以测量大型工件的半径R。量得两钢棒的圆心距为2d。则R等于 ( )
A、\frac{d^2}{4r} B、\frac{d^2}{4r^2} C、\frac{d^2}{r+d} D、\frac{r^2}{r+d}
这道题用直接解法来寻找正确答案也不难。但使用排除法会收到意想不到的效果。
首先排除B,因为B是无单位的量。再来考虑C,从图上看,当d为定值,r逐渐变小时,大型工件的半径会越来越大(无限变大)。但从式子 来看,当r变小时其值不会无限变大(最大才等于d)。故排除C。同样当r为定值,d逐渐变小时R应无限变小。而D的答案不具备这个特点,应排除D。所以选A。
d或r变小的过程,实际上就是一个动态的过程,就是一个运动的过程。没有一定想象能力的人是做不到的。所以用运动思想考虑问题一定会更有效地培养人的想象能力。
例8 如图9,P在直径AB上,∠1=∠2,试判断哪些线段相等?
对大多数同学来说,是不会发生什么错误的。但少数同学容易得出AP=GB的错误,因为他们判断线段相不相等,不是从本质上去判断,而是从图形的外观上去判断,看上去像相等那就一定相等了。
教师只要用运动思想启发学生,将直径AB及AB上点P看作定元素,使弦EF、CD绕P转动(保持∠1=∠2),那么AP为定长,而BG却是变量。于是在一般情况下AP≠BG(特殊情况时也可能刚巧相等)。
例9 如图10,弦CD、EF均垂直弦AB,且三等分AB,则 ( )
A、\stackrel\frown{AD}=\stackrel\frown{DF}=\stackrel\frown{FB} B、\stackrel\frown{AD}=\stackrel\frown{FB}<\stackrel\frown{DF} C、\stackrel\frown{AD}=\stackrel\frown{BF}>\stackrel\frown{DF} D、以上均不对
分析:从眼前的图形来看,A、B、C都有点像。但用运动方法将AB向上平移时,AD、BF迅速增加,而DF增加速度不大(AB运动时CD、EF也随之运动),并且平移至上半圆时DF反而减小了,可见应选C。
六、探求多解
不少数学问题用运动思想探求多解,要比代数方法优越得多。在运动过程中会发现满足条件的位置不止一处,多解就探求出来了。
例10 如图11,A、B、C、D是半径为8的⊙O上四个点,且这个四点构成等腰梯形, AB=DC=10。
(1)则等腰梯形的面积的值是( )
A、唯一的 B、有且只有二个 C、有且只有四个 D、有无数个
(2)若AB固定,弦CD的两端点可以在圆上滑动,则CD不能到达的位置有( )
A、一种 B、二种 C、四种 D、无数种
解:(1)将AB固定,DC看作一根棒,AD、BC看作橡皮筋,运动CD,发现梯形的大小改变。所以选D。(2)与(1)同法建模,移动CD时有如图12的四种位置不能到达。所以应该选C。
例11 等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/秒的速度运动,当P运动到PA与腰垂直的位置,求P点运动的时间。
多数学生是用画图的方法,画出一条与腰垂直的线段AP(如图13),然后进行计算。这样必定遗解。如果观察P从B至C移动的全过程,便会发现有两处的位置满足题设。正确的答案为7cm或25cm。
例12 已知直线y=kx+b过点P(1,–2),且与坐标轴围成的三角形是等腰直角三角形,求其解析式。
分析:本题若用代数方法求,甚是烦琐。若设想有一直棒绕P(1,–2)旋转,看有几种位置满足条件,然后把这些位置一一画出来(如图14),必定能收到事半功倍的效果。通过运动发现本问题有两解y=x–3和y=–x–1。
七、存在性研究
在几何问题中是否有这样位置的元素,使它满足一定条件。这类问题叫做几何中的存在性问题。解决这类问题的方法很多,用运动观察法不失为一种好方法。
例13 A城气象站测得台风中心在A城正西方300km的B处,以每小时 km的速度向北偏东60°的方向运动,距台风中心200km的范围是受台风影响的区域。
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,问影响的时间有多长?
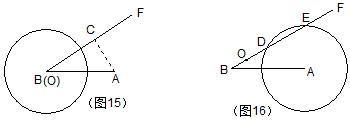
分析:如图15按题意画出图形。AB=300km,∠FBM=30°,⊙O的半径为200km。现设想⊙O的圆心O沿着BF方向移动,如果在移动过程中点A能落在⊙O内,则A城会受到台风影响。事实上A至BF的距离AC=150km小于200km,故一定会影响。为了解决第二个问题,可图按16画出半径为200km的⊙A。当台风中心O进入⊙A内A城便开始受到台风的影响。所以求影响时间的关键是在求⊙A在BF上截得的弦DE的长。
运动使我们看清问题的本质,运动使我们避免盲目的猜想。但这里有一个是不是善于运动的问题,如上例(1)中运动的对象是⊙O,(2)中运动的对象却是点O。(1)中的圆是动圆,(2)中的圆是定圆。不善于联系实际的人是难以想象的,没有灵活应变能力的人也难以想象的。
例14 是否存在m的值,使直线y=mx+4、直线x=1、直线x=4及x轴围成的直角梯形的面积为7?为什么?
分析这类问题的一般思路是先画图,后运动。看看直角梯形会出现在怎样的位置上。如图17,因直线y=mx+4始终过点A(0,4),故可将这条直线绕点A旋转,会在x轴的上下方各出现一个直角梯形。倘若⊿MBC(或⊿BCN)的面积小于7,m的值就存在,反之m的值就不存在.
事实上S△BCN>7,S△BCM<7,故知m的值是唯一存在的。
解题时先求出D(1,m+4),E(4,4m+4)。于是DB=m+4,EC=4m+4,BC=3。由题意,得\frac{3}{2} (m+4+4m+4)=7,m=-\frac{2}{3}。
八、探索型问题
探索型问题包括结论探索、条件探索、方法探索等。不少问题的探索是以运动作为先导,从运动中去发现规律,去猜想结论,从而探索出问题的结果。
例15 如图18,⊿ABC中B、C固定,A为动点。以AB、AC为边向形外作正方形ABDE及AFGC。过D、G向直线BC作垂线,垂足为H、P。
(1) HB和CP是否相等?
(2) DH+GP是否为定值?
(3) DG的中点O是否为定点?
分析:
(1)当A运动到BC的中垂线时,结论是肯定的。当A运动到∠ABC=30°时,可通过计算得出肯定的结论。当∠ABC=90°或∠ACB=90°时,可通过简单的证明来肯定结论。于是可猜想HB=CP!证明时可作△ABC的高线AQ,利用全等三角形来证明HB=AQ=CP。
值得注意的是当A运动使∠ACB为钝角时,结论仍然成立(如图19)。
(2)当(1)的结论作肯定的问答并得到证明后,容易发现DH=BQ,GP=QC,故DH+GP=BC,好像是定值。
但当点G在直线BC的另一侧时(如图19),DH+GP=BQ+QC是一个变量,所以不是定值。
(3)在几何画板上的动态显示表明,O点确实是一个定点。在图18中我们作OM⊥BC于M,则M是HP的中点也是BC的中点,且OM=\frac{1}{2}(DH+GP)=\frac{1}{2}BC,这说明点O是定点。
在图19中也作OM⊥BC于M,则有O为HP的中点,因HB=CP,故O为BC的中点,连PO并延长交DH于N,则OM是⊿HPN的中位线,OM=\frac{1}{2}(DH-GP)=\frac{1}{2}BC,同样可以说明点O为定点。
在上例各问题的探索中,如果不借助于运动是难以想象的。其中几何画板是一个好帮手。
通过以上18个例子,我们不难看到运动思想是如何解决数学问题的,“死”的图形是如何“活”起来的,模型是怎样想象出来的。我们可以说是不是善于用运动思想观察问题解决问题,是区分是不是具备分析问题和解决问题能力的重要标志。我们不难看出,培养学生的运动思想实际上是培养了他们的多种能力,除了想象能力外还有画图能力、审题能力等。要运动必先有图形,要画出正确的图形必先仔细审题。运动思想是把静止观点发生了质的飞跃,当学生有了这个飞跃后,他看问题的角度就与众不同,解决问题的方法也就层出不穷。
在众多数学思想中运动思想最容易受到冷落,这是因为许多人不重视运动思想,不习惯运用这种思想,甚至根本没有这种思想。虽然在教学中我比较重视渗透这个重要的数学思想,但使我困惑的是仍有一部分学生很难具备运动思想,他们常说想不到,是不是教学方法还不够好?有待于我进一步研究和探索。