用具体的数替代式子中的字母,从而解决问题,这种方法称为特殊值法。特殊值法主要用在选择题和填空题。
有不少数学题,用常规的方法解之会花费较多的时间,并且思考、推理、演算较为费劲。而运用“特殊值法”将会事半功倍,见效神速。
不少已经就读高中的学生来看我,我经常乘机抛出一个问题“初中解数学的方法中,在高中哪个最好用?”他们的回答都提到了“特殊值法”。可见“特殊值法”深受学生喜爱,是初高中通用的解题好方法、常用方法。
我的学生也写过类似的一篇数学小论文:
下面举例说明。
例1 已知点P(a,b)是双曲线y=\frac{c^2+1}{x}(c是常数)和直线y=-\frac{1}{4}x+1的一个交点,则a^2+b^2+c^2的值是 。
特殊值法:
取c=0,则P点坐标是(2,\frac{1}{2}),即a=2,b=\frac{1}{2},故a^2+b^2+c^2=4\frac{1}{4}.
常规方法:
由已知,得\frac{c^2+1}{x}=-\frac{1}{4}x+1,\frac{1}{4}x^2-x+c^2+1=0,
因为其有解,故\triangle\ge0,即-c^2\ge0,c=0.
此时方程的解是x_1=x_2=2,即a=2,从而求得b,故a^2+b^2+c^2=4\frac{1}{4}.
说明:由于本题c的值是唯一的,所以运用特殊值法有点碰运气了。
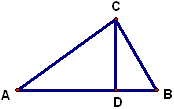
例2 在Rt△ABC中,CD是斜边AB上的高,∠A=30度,那么下列结论正确的是( )
A、3AD^2=4BC^2 B、AB^2=3AC^2
C、AC^2=10BD^2 D、16CD^2=3AB^2
解:用特殊值法,取DB=1,那么BC=2,AC=2\sqrt{3},AD=3,CD=\sqrt{3},AB=4。
将这些值一一代入四个选项,只有D正确。
例3 已知非零实数满足a>\frac{1}{a},那么a的取值范围是 ( )
A、a<-1 B、0<a<1 C、a>1 D、a>1或-1<a<0
解:在A中,取a=-2,不符合a>\frac{1}{a},
在B中,取a=\frac{1}{2},不符合a>\frac{1}{a},
在C中,取a=2,符合a>\frac{1}{a},
在D中取a=2,a=-\frac{1}{2},都符合a>\frac{1}{a},
故选D.
例4 已知a是非零实数,则下列不等式一定成立的有( )
a^2+1>1,1-a^2<0 ,a+\frac{1}{a}>1 ,|a+\frac{1}{a}|\ge2,|a-1|\le{|a|+1}.
A.1个 B.2个 C.3个 D.4个
解:因为a≠0,故可以取特殊值a=1或-1,结果除了2、3两个不符合外,其余都符合。故选C.
特殊值法使用不当也会造成错误。
例5 已知非零实数x、y满足x-\sqrt{xy}-2y=0,则\frac{x}{y}= 。
错解:取x=4,y=1,则原式=4。
正解:已知条件变形得,x-2y=\sqrt{xy},平方得,x^2+4y^2-4xy=xy,
即x^2-5xy+4y^2=0,解之x=4y或x=y,所以\frac{x}{y}=4或1.
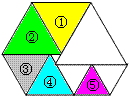
例6 如图是由9个等边三角形拼成的六边形,若图中最小等边三角形的边长是a,最大的等边三角形边长为b。现有下列说法:
(A)标号为①的等边三角形的边长可以表示为b-a;
(B)标号为②的等边三角形的边长可以表示为2a+b;
(C)标号为③的等边三角形的边长可以表示为b-3a;
(D)标号为④的等边三角形的边长可以表示为\frac{2b}{3};
(E)标号为⑤的等边三角形的边长可以表示为\frac{b}{2}.
以上说法正确的的是 (填写字母序号)。
错解:(A),(E)显然正确。标号为①②的等边三角形的边长应该相等,但取a=1.b=4,却不相等。(C)也不正确。对于(D),仍取a=1.b=4,标号为④的等边三角形的边长应该是2,但计算\frac{2b}{3}=\frac{8}{3},故不正确。所以正确的是:(A),(E)。
正解:由代数计算可知,标号为⑤的等边三角形的边长可以表示为b-3a,所以b-3a=b÷2,故b=6a,所以可以取a=1,b=6,验证后得知:(A),(D),(E)正确。
《“特殊值法”在解题中的应用》有一个想法