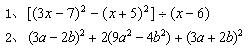一、引言
提高初中数学课堂教学效益的途径比较多,其中开设公开课和评课研讨是重要的途径之一。近年来,“专家引领、同伴互动、个人反思和行为跟进”的行动教学模式备受关注,但由于实际教学中受人力、物力和时间等条件的限制,我们采用“一课二听”的教研活动形式,这是一种比较受欢迎的校本教研方式,即听好一位教师的课后,听课者(有专家参与)从教学理念、教学方法和一些细节问题上提出改正意见,由上课教师调整教学设计后再上一节同样内容的课,由此来切身体验课堂教学效益是怎样提高的。2006年5月24日,我们学校年轻的数学教师沈晔有幸成为这种形式教研活动的受益者。听课者是宁波大学数学教育研究博士、宁波市教育学院的老师、宁波市初中数学骨干教师高级研修班的学员。下面用案例形式对本次活动进行回顾和反思。
二、“一课二听”教研活动案例
沈晔老师是我校教龄不到一年的年轻教师,该教师平时勤奋好学,为了促进年轻教师专业成长,学校不但安排师徒结对,还经常进行听课帮带。刚进校时连怎样备课、上课都不知道,后来由于本人好学,进步较快。当学校得知有这么一个机会,就立即想到沈晔应该得到尝试。
她上课的内容是《因式分解复习课》。先由其自己进行教学设计、备课,上午第1节在105班上了第一次课,第2节课大家坐在一起,围绕着如何上好这节课进行热烈地讨论,专家们就如何改进教学设计提出了许多好的建议。在第3节课沈老师根据专家的建议进行第二次备课,修改课件。第4节课在108班又上了同样内容的课。
1、第一节课教学过程概述
本节《因式分解复习课》采用了传统的教学模式,整节课可以分为知识回顾、因式分解练习、因式分解应用和小结四个模块。
| 模 块 | 内 容 | 时间 | 课堂实录 |
| 知识回顾 | 1.什么叫做因式分解?(复习因式分解的概念以及因式分解与整式乘法的关系)2.我们学了哪些因式分解的常用方法?(提公因式法 ,公式法,十字相乘法 ) 3.因式分解的一般思考步骤是怎样的?(“提”、“套”、“查”) | 6分钟 | 教师叫个别学生回答问题,气氛有点沉闷,大多数学生作为旁听者,参与面不大 |
| 练 习 | 练习1、以下从左到右的变形中,哪些是因式分解?(1)(a+2)(a-2)=a2-4;(2)-x2+xy-xz=-x(x-y+z);(3)x+1=x(1+1/x);(4) 8a3bc=2a2·4abc(5)a2-b2=(a+b)(a-b);(6) m2+m-4=(m+3)(m-2)+2。 | 4分钟 | 教师让学生先观察,再叫学生一一回答,当学生讲错时,教师将以纠正 |
| 练习2、把下列各式因式分解:(1) 3ay-3by+3y;(2) -4a3b2+6a2b-2ab;(3) 25-16x2;(4) x2-14x+49 | 5分钟 | 教师既在大屏幕上打出题目,又将题目抄在黑板上,让4位学生上来板演,2分钟20秒后板演完毕。 | |
| 练习3、把下列各式因式分解:(1) 5m(a-b)4-4m2(b-a)3;(2)9(x-y)2-(x+y)2;(3)(x+y)2-6(x+y)+9;(4)3x3-12x2y+12xy2;(5)4(x-1)2(3x-2)+2-3x | 10.5分钟 | 大屏幕打出题目后,教师让全体学生在自己草稿纸上进行运算。然后教师边讲解边板演,偶尔叫个别学生回答问题。 | |
| 应 用 | 计算(1)(2mp-3mq+4mr)÷(2p-3q+4r);(2)[(3x-7)2-(x+5)2]÷(x-6) | 6分钟 | 先逐一叫学生板演,再进行讲解,其中做第2题的学生因题目有难度而没能完成。 |
| 解方程(1)3x2=4x;(2)x2=(2x-5)2 | 6.8分钟 | 第1题学生板演后再讲解,但没有讲降次的一般方法 | |
| 利用因式分解计算:(1)57×99+44×99-99;(2)9752-252;(3)8002 -1600×798+7982 | 6分钟 | 教师自己板演 | |
| 小结 | 因式分解的“四个注意”一、首项有负常提负;二、各项有公先提公;三、括号里面分到底;四、提净分完连乘式。 | 2.5分钟 | 至此上课已经用了44分18秒,所以小结就很匆忙了。教师赶紧说:下面老师送给你们四句话。 |
2、第一节课后专家点评
①复习引入单调,建议采用边练习边总结的办法,导入的内容应该在操练中体现。
②讲解不够深入,没有提高到思想方法上来,如整体思想、降次方法等。
③要注意变式,如解方程3x2=4x,可以变式为3x2-4x=0、3x2-4x=-1以及x(3x-4)=-1等。
④教师讲得太多,学生动、说得太少。要扩大学生投入的面,积极关注学生的认知投入、行为投入和情感投入。
⑤时间安排不够合理,详略不当,小结匆忙。
3、第二节课教学过程概述
经过专家的指点,第二节课对上述5个方面进行了改进,课堂教学过程见下表。
| 模 块 | 内 容 | 时间 | 课堂实录 |
| 练 习 | 练习1、以下从左到右的变形中,哪些是因式分解?(1)(a+2)(a-2)=a2-4;(2)-x2+xy-xz=-x(x-y+z);(3)x+1=x(1+ );(4) 8a3bc=2a2·4abc;(5)a2-b2=(a+b)(a-b);(6) m2+m-4=(m+3)(m-2)+2。 | 3分钟 | 先出示上一节课的练习1,叫学生逐一回答,完成 练习1后复习“什么叫做因式分解”。 |
| 练习2、把下列各式因式分解:(1) 3ay-3by+3y;(2) -4a3b2+6a2b-2ab;(3) 25-16x2;(4) x2-14x+49 | 4.5分钟 | 接着出示上一节课的练习2,学生先独立完成,教师再逐一叫学生回答解答方法。完成例2后复习“因式分解的一般方法” | |
| 练习3、把下列各式因式分解:(1) 5m(a-b)4-4m2(b-a)3;(2)9(x-y)2-(x+y)2;(3)(x+y)2-6(x+y)+9;(4)3x3-12x2y+12xy2;(5)4(x-1)2(3x-2)+2-3x | 12.5分钟 | 练习3每道小题由两位学生板演,每做完一题就进行讲解。后问学生有什么感受,有一位学生回答:要检查结果有没有分解到底。教师说出了自己的感受:换元思想。 | |
| 应 用 | 利用因式分解计算:(1)57×99+44×99-99;(2)9752-252;(3)8002 -1600×798+7982 | 7分钟 | 由学生板演,教师讲评。 |
| 解方程(1)3x2=4x;(2)x2=(2x-5)2;(3)x2+4x=12 | 8分钟 | 由学生板演后再讲解,并总结了降次的一般方法 | |
| 计算(1)(2mp-3mq+4mr)÷(2p-3q+4r);(2)[(3x-7)2-(x+5)2]÷(x-6) | 7.5分钟 | 学生板演,再进行讲解,其中第2题由2位学生上来板演,第2位学生做对了。 | |
| 小结 | 因式分解的“四个注意”一、首项有负常提负;二、各项有公先提公;三、括号里面分到底;四、提净分完连乘式。 | 2.5分钟 | 由于时间充裕,所以小结很从容,但内容与前一节课一样。 |
4、课后的形成性测评
授课的两个班级基本在同一层次上,学习情况相近。课后对两个班都进行了评价,评价题目是:
(1)因式分解(3x-5y)2-(x-3y)2;(3分)
(2)已知a2-b2=40,a+b=8,求a的值;(2分)
(3)解一元二次方程x(x+1)=2;(2分)
(4)用三种方法填空,其中横线上填单项式,括号里填多项式。(3分)
4x2+ +1=( )2;4x2+ +1=( )2;4x2+ +1=( )2
评价结果是:
| 0分 | 1分 | 2分 | 3分 | 4分 | 5分 | 6分 | 7分 | 8分 | 9分 | 10分 | 总人 | 平均 | |
| 105班 | 2人 | 2人 | 0人 | 6人 | 7人 | 5人 | 1人 | 8人 | 3人 | 1人 | 0人 | 35 | 4.8 |
| 108班 | 2人 | 2人 | 1人 | 0人 | 6人 | 2人 | 4人 | 11人 | 2人 | 1人 | 2人 | 33 | 5.6 |
明显看出,第二节课的效果比较好。
三、对本次活动的反思
1、二节课的前后变化
第一节课导入无味,讲解时详略不当,常有累赘之感。教师讲得多,学生动得少,课堂气氛较为沉闷,缺乏活泼、生动的场面。整节课没有高潮,缺乏悬念,所提问题过于肤浅,没有层次感。
经过专家指点,第二节课有所改观,具体反映在以下几个内容。
- 导入穿插在例1、例2中,既少花时间,又使学生不觉乏味。
- 增加板演,学生参与率高。
- 讲解时详略得当,减少了重复感。
- 时间安排更加合理,使得每个环节都比较充裕。
- 解一元二次方程类型更多,能点明降次的基本方法。
2、教学中仍存在的问题
①整节课没有高潮,缺乏起伏,太传统
②学生参与面还不够大
③题型缺乏变化
④设问不能引起认知冲突
⑤教学模块的设置不够清晰
3、“一课二听”活动的不足
①一个半天内,两节课之间往往只有两节课,一节课点评,一节课修改教学设计,时间太仓促,于是第2节课的效果不是太理想,以至还存在上述5个问题。
②不是每个学校都能做到“专家引领”,这样也只能靠“同伴互助”了,活动的收效会少一点。
③执教者的基本功太好或太差都会影响活动的效果,于是执教者的选择比较困难。
4、对本课教学设计的进一步建议
教学设计的关键是在于教学目标的定位,作为因式分解的复习课,教学目标不应该仅仅定位于复习因式分解的概念和方法,更应拓展到培养学生良好的思维习惯和多种数学思想,将因式分解应用到更加广泛的领域。教师讲得少,学生动得多,设置一些有新意的问题,让学生进行讨论,让课堂活起来。
四、本人设计的《因式分解复习课》教案。
同学们,我们已经学完了因式分解,今天我们来复习一下。下面是两位同学做题的过程,哪位同学做错了?错在哪里?
练习1
甲同学做的题是:计算3(x2-2xy-y2)-2(x2-3xy-y2)
解:原式= 3x2-6xy-3y2-2x2+6xy+2y2=x2-y2=(x+y)(x-y)
乙同学做的题是:计算(3x-2y)2-(2x-3y)2
解:原式=[(3x-2y)+(2x-3y)][(3x-2y)-(2x-3y)] =(5x-5y)(x+y)
=5(x+y)(x-y)=5x2-5y2
点评:上面沈老师的课中,练习1“以下从左到右的变形中,哪些是因式分解?”其实没有多大必要,有些变形虽然不是因式分解,但掌握这种变形也挺有必要。上面甲同学错在最后一步,这种错误倒是学生中较为常见的,是因式分解概念不清楚所致。乙同学的做法是正确的,这种利用因式分解来帮助我们进行整式的乘法的做法,在学生中少之又少。
同学们,因式分解时我们常有人发生错误,原因是多种多样的,下面请同学谈谈你在各种错误中,发生最多的错误是哪一种?
点评:让学生自己说自己的错误,能加强对错误的重视。可能较多的学生会说:没有分解到底、看不出分解的方法。为下面的练习2作好准备。
练习2
下列因式分解哪些是错误的?将错误改正。
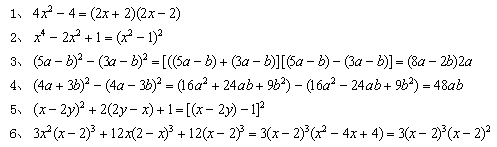 点评:上述6道题除了第4题正确外,其余都有问题。1、2、3是没有分解到底,3、5、6在书写上不符合要求,即单项式应写在多项式前面,结果中不能含有中括号,相同的因式要运用同底数幂相乘的法则。这5道题的错误在平时作业中发生率极高。而第4题是利用乘法进行因式分解,这种做法在学生也是不多的,其实这是一种较好的方法。
点评:上述6道题除了第4题正确外,其余都有问题。1、2、3是没有分解到底,3、5、6在书写上不符合要求,即单项式应写在多项式前面,结果中不能含有中括号,相同的因式要运用同底数幂相乘的法则。这5道题的错误在平时作业中发生率极高。而第4题是利用乘法进行因式分解,这种做法在学生也是不多的,其实这是一种较好的方法。
同学们,要避免上面几种错误也不难,你只要牢牢记住:
先要提取公因式,然后试试用公式,留神结果能否分,分解到底要牢记。
上面6道题中有4道要分解2次,如果一道题要分解3次就更难了。现在要你考考别人,每个同学出一道因式分解的题,要求需要分解3次,然后前后4个人交换题目解一下。
点评:自己出题让别人做,每个学生一定很带劲,但有难度。可以让先编好题的同学说一说编题的经验,使其他同学有个借鉴。到这里可能会出现本课的第一个高潮。
好!下面我要看看大家因式分解的应用能力。
练习3
计算下列各题
点评:借助因式分解进行整式的运算是因式分解应用的一个方面,而利用因式分解进行有理数的计算(如8002 -1600×798+7982),在可以使用计算器的今天已经没有必要了。
练习4
点评:因式分解是解一元二次方程的重要方法,但在已经删去了十字相乘方法以后,像x2+4x=12这样的方程就应该放到以后去做了。
练习5
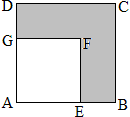 如图正方形ABCD和正方形AEFG有公共顶点A,它们的周长和为12,E在AB上,G在AD上,阴影部分的面积是6,求EB的长。
如图正方形ABCD和正方形AEFG有公共顶点A,它们的周长和为12,E在AB上,G在AD上,阴影部分的面积是6,求EB的长。
练习6
(1)当a=-3,b=2时,求输出的值;
(2)当输出的值为12时,问整数对(a,b)有哪几种可能?
(3)是否存在这样的整数对(a,b),使当输出的值为24?
点评:做第(2)题会有困难,可以让学生4人一组进行讨论,不会做也可以“凑”,看哪组“凑”出的整数对(a,b)多,估计学生是“凑”不全的,这时就到了本课的第二个高潮。教师归纳时用因式分解的方法,即a2-4b2=(a+2b)(a-2b),再列表如下:
| a+2b | 6 | -6 | 2 | -2 |
| a-2b | 2 | -2 | 6 | -6 |
这样会产生4对整数对(a,b)(注:(a+2b)和(a-2b)必须同奇偶)。而第(3)题的答案是不存在的。
小结:
1、通过今天的复习我们更加清楚地知道,因式分解要注意的事项是 。
2、下面两句话是否正确
(1)我们可以利用因式分解进行整式计算
(2)我们可以利用整式计算进行因式分解
3、今天在我们所做的题目中,体现了较多的数学思想,如 , 等。