切线的判定教材里只有一个例题,证明方法是先连一条半径,再证明这条半径和要判定的直线垂直。这种方法简单的说就是“先有r再证d”。而事实上切线的判定共有三种类型。
一、先有r再证d
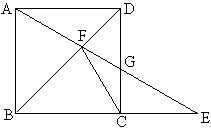
例1 如图,正方形ABCD中,E在BC的延长线上,AE交BD、CD于F、G,求证:FC是\triangle{GCE}的切线。
分析:C已经是FC和圆的公共点了,所以连圆心O和C,得到的OC就是半径了,只要证明{OC}\perp{FC}即可。这就是“先有r再证d”的类型,至于垂直的证明就不难了。
二、先有d再证r
还有一种类型是要判定的切线与圆有没有公共点不已知,可以作垂线后再证明这条垂线段等于半径,这种方法简单的说就是“先有d再证r”。下面举例说明。
例2 如图\triangle{ABC}中,AB=AC,点O是BC的中点,\odot{O}与AB切于点D,求证:\odot{O}与AC也相切。
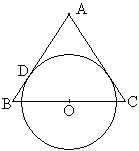
分析:\odot{O}与AC有没有公共点未知,所以不能连结得半径,只能过O作AC的垂线段得距离d,再证明这个距离等于半径r,故属于“先有d再证r”的类型。
三、d、r都要证
还有一种切线的判定,事先既不能得到半径,也不能得到距离,也就是半径距离都要证明的类型,这一种可以说成是“d、r都要证”。请看下例:
例3 如图,\triangle{ABC}中,AB=AC,\angle{B}=30^\circ,O、D将BC三等分,以OB为圆心画\odot{O},求证:\odot{O}与AC相切。
分析:\odot{O}与AC是否有公共点不已知,按已知可以证明A就是切点,所以过O作AC的垂线的话,还得证明垂足和A重合,这样的证明尽量避免。于是,还是连结AO,证明AO既是半径,又是距离。故属于“d、r都要证”的一类。
具体的证明方法是:连结AO,作{AE}\perp{BC}于E,设AB=6,则BC=6\sqrt{3},所以OE=\sqrt{3},因为AE=\frac{1}{2}AB=3,所以AO=2\sqrt{3}=BO。至于{AO}\perp{AC}的证明不难了,就留给读者思考。
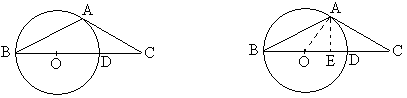
@潘
谢谢潘老师来坐沙发,有你的光临陋室顿生灵气。
我还是坚持我的观点,例3不可以归结为第一种的。因为连了OA却不知是半径,而第一种的半径是已知的。
黄老师:今天看了您的诸多博文,佩服您的经验和智慧,感动您的勤奋和执着,向你学习!
关于切线的证明,我常常把它归纳为2种方法:
1.连半径证垂直。(明确或可证线上有点在圆上)
2.画垂直证半径。(不清楚线上是否有点在圆上)
学生很容易进行操作,效果不错。
以上例3,可归结为第一种,主要要证OA=OB,最简单的方法就是利用三角函数,求得∠AOE为 60°,则点A在圆上和垂直几乎同时得到。
与您商榷。