在这里,我会陆续展示一些平时收集的难题,供大家参考。我的解答可能不是最好的,请你指点。这些题目也不一定是难题,也不一定很经典,只能说这些题是我较喜欢的,喜欢的原因是我很佩服命题者。说不定今天你看到的这篇文章,已经比上次新增了几题。
例1
如图所示,一长方形被分割成9个互不交叠的正方形,如果该长方形的长与宽为互质的非零自然数,那么此长方形的周长为 。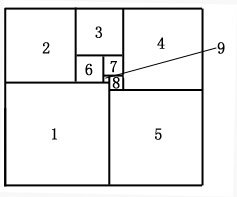
解:如图,设正方形6的边长为x,正方形7的边长为y,那么
正方形3的边长为x+y,
正方形2的边长为x+x+y=2x+y,
正方形9的边长为x-y,
正方形8的边长为y-(x-y)=2y-x,
正方形4的边长为(x+y)+y+(2y-x)=4y,
正方形1的边长为(2x+y)+x+(x-y)=4x,
正方形5的边长为(2y-x)+4y=6y-x或(2x+y)+4x-4y=6x-3y,
∴6y-x=6x-3y,y=\frac{7}{9}x,
∴长方形的两边长分别是(2x+y)+4x=6x+y=\frac{61}{9}x,4x+6y-x=3x+6y=\frac{23}{3}x,
为了使\frac{61}{9}x和\frac{23}{3}x互质,只能取x=9,这时边长为61和69,周长为260。