学生练习中有一道二次函数应用题:
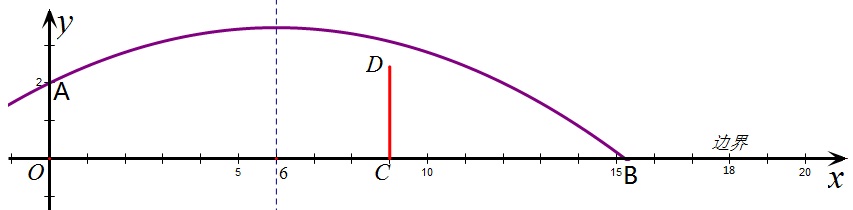
(安徽2012年)23.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)^2+h.已知球网CD与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。
本题有3个小题,前2个小题略。
我做第(3)题的方法是采用极端原理。
解:当抛物线过D点时,可以将A(0,2)及D(9,2.43)代入,得
\begin{cases} 36a+h=2\\ 9a+h=2.43 \end{cases},解得\begin{cases} a=-\frac{43}{2700}\\ h=\frac{193}{75} \end{cases},
当抛物线过边界(18,0)时,可以将A(0,2)及B(18,0)代入,得
\begin{cases} 36a+h=2\\ 144a+h=0 \end{cases},解得\begin{cases} a=-\frac{1}{54}\\ h=\frac{8}{3} \end{cases},
因为\frac{8}{3}>\frac{193}{75},所以\frac{193}{75}\le{h}\le\frac{8}{3}.