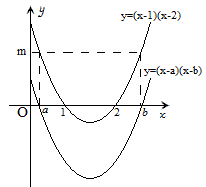有许多数学问题,用函数图象解决优于其它方法, 而这恰恰是许多人想不到的。究其原因是缺乏函数思想和数形结合思想。
我相信,当你看完以下题目的解答后,一定会收到启发,利用函数图象解决问题的方法便会成为你有力的工具。
一、函数图象解决方程问题
例1 已知关于x的一元二次方程(x-1)(x-2)=m(m>0)的两个解分别是a和b,那么关于x的一元二次方程(x-a)(x-b)+m=0的两个解是什么?
解:构造三个函数如下:
y_1=(x-1)(x-2),y_2=(x-a)(x-b),y_3=(x-a)(x-b)+m,前两个函数图象如下:
由图可知,函数y_2=(x-a)(x-b)的图象可以看作是函数y_1=(x-1)(x-2)图象向下平移m个单位得到的。
再将函数y_2=(x-a)(x-b)的图象向上平移m个单位就得到y_3=(x-a)(x-b)+m,也就是y_1=(x-1)(x-2),
所以一元二次方程(x-a)(x-b)+m=0的解就是(x-1)(x-2)=0 的解,即解为x_1=1,x_2=2.