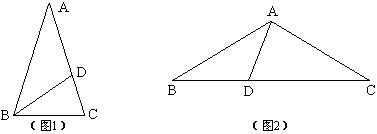我们知道30°,45°,60°是非常特殊的锐角,它们具有许多性质。不过你是否知道,36°也是一个比较特殊的锐角,它的特别之处可以用“美”来形容。国旗上的五角星的锐角就是36°,正十边形的中心角就是36°,36°的2倍是72°、3倍是108°,72°和108°又是互补的,36°与108°的一半又是互余的……
1、含36°的等腰三角形
如图1,若等腰△ABC的顶角∠A=36°,作底角的平分线BD,那么BD分原三角形得到两个较小的等腰三角形,其中一个和原三角形相似,BC^2=CD{\times}CA,D是AC边的黄金分割点,底边与腰的比是黄金比。
如图2,等腰△ABC的底角∠B=∠C=36°,作∠BAD=36°交BC于D,那么AD分原三角形得到两个较小的等腰三角形,其中一个和原三角形相似,AB^2=BD{\times}BC,D是BC边的黄金分割点,腰与底边的比是黄金比。
2、36°角的尺规作图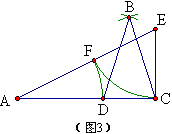
如图3,作法是:(1)任作一条线段AC;(2)作AC的黄金分割点D;(3)分别以D、C为圆心、AD长为半径画弧,两弧交于B;(3)连结BC、BD。结论:∠DBC=36°.
证明:连AB即为图1,因为BC^2=AD^2=DC{\times}AC,所以△BDC∽△ABC,∵AB=AC,∴BC=BD,设∠BAC=x°,则∠ABD=∠BAC=∠DBC=x°,∠BDC=∠BCD=2x°,列方程可得x=36°.
3、36°角的三角函数计算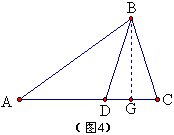
如图4,已知AB=AC,∠A=36°,作高BG,设AC=1,则AD=BD=\frac{\sqrt{5}-1}{2},DC=\frac{3-\sqrt{5}}{2},DG=\frac{3-\sqrt{5}}{4},AG=\frac{3-\sqrt{5}}{4}+\frac{\sqrt{5}-1}{2}=\frac{\sqrt{5}+1}{4},所以cos∠A=\frac{AG}{AB}=\frac{\sqrt{5}+1}{4}。其余三角函数的值同理可求。
4、正五边形的尺规作图
所有正五边形的尺规作图都与36°的性质有关,也就是与黄金分割有关,也就是与\frac{\sqrt{5}-1}{2}有关。
(1)已知正五边形的一边作正五边形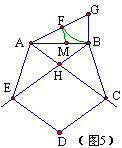
如图5,已知线段AB,作正五边形ABCDE。
作法:①作AB的黄金分割点M;②以A、B为圆心AM为半径画弧,两弧交于H;③以A、B为圆心AB为半径画弧,两弧分别交AH、BH的延长线于C、E;④分别以E、C为圆心AB为半径画弧,两弧交于D. 结论:五边形ABCDE即为所求。
证明过程留给读者(下同)。
(2)已知正五边形的对角线,作正五边形
如图5,已知线段BE,作正五边形ABCDE。
作法:①作BE的黄金分割点H;②以E、B为圆心EH为半径画弧,两弧交于A;③以B为圆心AB为半径画弧,交AH延长线于C;④分别以E、C为圆心AB为半径画弧,两弧交于D. 结论:五边形ABCDE即为所求。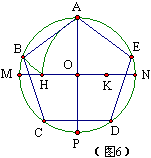
(3)作已知圆的内接正五边形
已知圆O,作圆O的正五边形ABCDE.
作法:①作圆O互相垂直的直径MN和 AP. ② 平分半径ON,得OK=KN. ③以 K为圆心,KA为半径画弧与 OM交于 H, AH即为正五边形的边长. ④以AH为弦长,在圆周上截得A,B,C,D,E各点,顺次连接这些点即得正五边形.
我想你一定想到了作已知圆的正十边形的方法了,对!还是靠黄金分割点,作半径的黄金分割点哦。
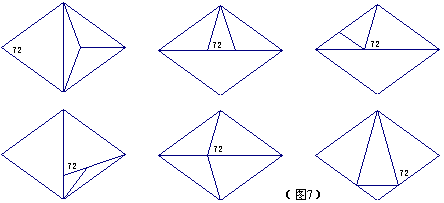
5、与36°有关的其它问题
(1)将含有108°角的菱形分割成4个等腰三角形
有如下一些分割方法,几乎都与36°、72°有关
我马上就可以仿照上题编一道题:将含有36°角的菱形分割成4个等腰三角形。估计方案不会少。
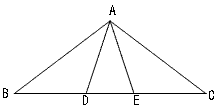
(2)如图,在△ABC中,∠B=∠C=36°,∠ADE=∠AED=2∠B,由这些条件你能得到哪些线段相等?请证明你的结论。
解:由36°及72°的特点,不难得到两组线段相等:
①AB=BE=CD=AC;②BD=AD=AE=EC.
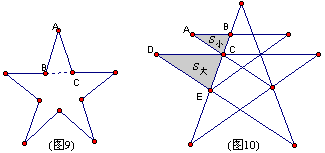
(3)某装饰公司要在如图9所示的五角星形中,沿边每隔20厘米装一盏闪光灯。若BC=(\sqrt{5}-1)米,则需安装闪光灯( )
(A)100盏 (B)101盏 (C)102盏 (D)103盏
解:由BC=\sqrt{5}-1 ,及△ABC是黄金三角形,得AC =2,
∴五角星形的周长为2×10 =20米,∵20÷0.2=100,∴需要安装100盏灯,故应选A.
(4)如图10是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星—这一光明的象征联系在一起,设结构图中的两个阴影三角形的面积S小=S1,S大=S2,那么S1与S2之比为 ( )
(A)\frac{1}{3} (B)\frac{1}{3} (C)\frac{\sqrt{5}-1}{2} (D)\frac{3-\sqrt{5}}{2}
∵△DEC是黄金三角形,∴CE:DE=(\sqrt{5}-1),即AC:DE=(\sqrt{5}-1) ,
∵△ABC∽△DEC,∴\frac{S_1}{S_2}=(\frac{\sqrt{5}-1}{2})^2=\frac{3-\sqrt{5}}{2} ,故选D。