我们知道，等腰三角形的顶角平分线垂直平分底边。反之，当题设中出现角平分线时，如能联想到等腰三角形，往往可以很快沟通思路，提高解题效率。这里略举几例。
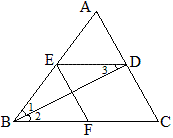例1 如图，在△ABC中，∠B的平分线交AC于D，DE//BC交AB于E，EF//AC交BC于F，求证：BE=FC。
证明：∵DE//BC，∴∠2=∠3. 又∵ ∠2=∠1, ∴∠1=∠3. ∴ BE=DE.
∵ DE//BC, EF//DC，∴ 四边形CDEF为平行四边形. ∴ FC=DE， ∴ BE=FC.
本题虽然比较简单，但细心的同学可以从中注意到一个有用的基本图形，如图，M为∠AOB的平分线上的一点，MN//OA交OB于N，则ON=MN，即△MON为等腰三角形。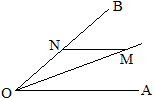
归纳出：角平分线+平分线→等腰三角形.
如能抓住这个基本的图形,将对解题带来很大的方便。
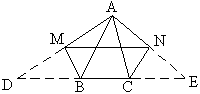
例2 如图△ABC中，∠A=90○，过顶点A平行于BC的直线与∠ABC，∠ACB的平分线交于E、D两点。若AC=6，BC=10，求DE的长。
简析：由基本图形可知△ABE、△ACD均为等腰三角形，因此DA=AC、AB=AE. ∴DE=DA+AE=AC+AB.
题中AC为已知，只要求出AB问题就容易解决。
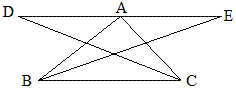
例3 如图，已知BM、CN分别是△ABC的外角平分线，且AM⊥BM，AN⊥CN，垂足为M、N。求证：1、NM//BC；2、MN=\frac{1}{2}（AB+BC+CA）.
证明 延长AM、AN交直线BC于D、E。
∵ BM平分∠ABD，AM⊥BM，∴ △ABM≌△DBM（ASA），∴ AB=DB.
即△ABD为等腰三角形，∴M为AD中点。
同理可证，AC=CE，N为AE中点。
∴MN为△ADE的中位线，∴MN//BC，
∴MN=\frac{1}{2}DE=\frac{1}{2}（DB+BC+CE）
=\frac{1}{2}（AB+BC+CA）.
本题中的关键是由题材设中角平分线，角平分线的垂线构造等腰三角形。
其基本图形如图.
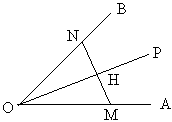
OP为∠AOB平分线，H为OP上一点，
过H作MN⊥OP交OA、OB于M、N，
则OM=ON，即△OMN为等腰三角形。
归纳它的模型为：角分线+垂线→等腰三角形。