在解答数学问题时,常常有一些问题需要从整体的角度来探究。如果只从局部的角度来研究问题,就不能使问题得到简化,反而使计算麻烦。如果我们把要解决的问题看作一个整体,研究问题的整体结构或对问题作出整体处理,常常能得到简洁、巧妙的解法。
运用整体思想解题的方法有很多种,常见的有:
1. 整体换元
它一般是根据已知条件求代数式的值。有时直接代入求值非常不方便,但是若把已知条件经过变形看作一个“整体”再代入,这样就能避免计算时的困难。
例1 分解因式:(a+b-2ab)(a+b-2)+(1-ab)²
解:设a+b=m,ab=n,则
原式=(m-2n)(m-2)+(1-n)²
=m²-2m-2mn+4n+1-2n+n²
=m²-2m(n+1)+(n+1)²
=(m-n-1)²
=(a+b-ab-1)²
对于这种复杂的多项式,如果把它展开后,再添项、拆项,就会比较麻烦。但如果把其中某些部分看作整体,用新的字母代替,不仅可以使原式得到简化,而且能使原式的特点更加明显。
2. 整体求解
在解方程时,可以把几个未知数看作为一个整体考虑,这样就可以简化解题过程。
例2 有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需31.50元;若购甲4件,乙10件,丙1件,共需42.00元。现在购甲、乙、丙各一件,共需多少元?
解:设购甲一件需x元,购乙一件需y元,购丙一件需z元,
则\left\{\begin{matrix} 3x+7y+z=31.50\\ 4x+10y+z=42.00\end{matrix}\right.。
设x+y+z=m(3x+7y+z)+n(4x+10y+z) =(3m+4n)x+(7m+10n)y+(m+n)z
∴ \left\{\begin{matrix} 3m+4n=1\\7m+10n=1\\m+n=1\end{matrix}\right.,∴\left\{\begin{matrix} m= 3\\ n=-2\end{matrix}\right.。
所以x+y+z=3(3x+7y+z)-2(4x+10y+z)=3×31.50-2×42.00=10.50
答:共需10.50元。
这是一道通过列方程体现整体思想的题目。如果想分别求出甲、乙、丙各一件的价钱,这是不可能的。我们可以把甲、乙、丙各一件共所需的钱,看作一个整体。这样会使计算简便很多。
3. 整体求值
有些数学问题,在分类讨论时会有多种情况,但如果整体求值,就可以避免分类讨论。
例3 已知a.b.c是常实数,x.y是任意实数,
A=(a-b)x+(b-c)y+(c-a)
B=(b-c)x+(c-a)y+(a-b)
C=(c-a)x+(a-b)y+(b-c)
求证:A.B.C不能都是正数,也不能都是负数。
证明:∵A=(a-b)x+(b-c)y+(c-a), B=(b-c)x+(c-a)y+(a-b), C=(c-a)x+(a-b)y+(b-c),
∴ A+B+C=(a-b)x+(b-c)y+(c-a)+(b-c)x+(c-a)y+(a-b)+(c-a)x+(a-b)y+(b-c)
=(a-b+b-c+c-a)x+(b-c+c-a+a-b)y+(c-a+a-b+b-c)=0
∵A.B.C是常实数.
∴A.B.C不能都是正数,也不能都是负数。
本题如果用分类讨论思想,则须分一正二负、一负二正、三正和三负四种情况,而x、y为变量,且a、b、c的大小关系不明确,难以着手。但如果用整体求和,即可证得A+B+C=0,从而使问题得到解决。
4. 整体转化
从问题的表面上需要求出各个量的值,但事实上这些量并不需要求出来。如果把这些量转化为整体,这样解题也许会方便很多。
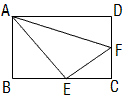 例4 如图,矩形ABCD,E、F分别是BC、CD上的点。若△CEF,△ABE,△ADF的面积分别为3、4、5,求△AEF的面积。
例4 如图,矩形ABCD,E、F分别是BC、CD上的点。若△CEF,△ABE,△ADF的面积分别为3、4、5,求△AEF的面积。
解:设BC=x,AB=y
∵S_{\triangle{ABE}}=4, ∴BE=\frac{8}{y},∴EC=x-\frac{8}{y},
同理CF=y-\frac{10}{x}. ∵矩形ABCD, ∴∠C=90°,
∵S_{\triangle{CEF}}=3, ∴(x-\frac{8}{y})(y-\frac{10}{x})=6.
∴xy+\frac{80}{xy}-24=0,(xy)²-24(xy)+80=0,
(xy-20)(xy-4)=0, ∴xy1=20,xy2=4
检验:当xy1=20时,分母不为0,当xy2=4时,分母不为0,∴xy1=20,xy2=4,
∵xy>12, ∴xy2=4舍去, ∴xy=20, ∴S_{\triangle{AEF}}=20-3-4-5=8.
这道题虽然列了方程,但是却不用解出x、y分别的值,而是直接求出xy的值,计算起来比较简单。在这里就是把xy,也就是一个矩形的面积看做了一个整体。
数学中,运用整体思想的范围是非常广泛的,它不仅能用于代数计算、因式分解、解方程,还可以用于许多几何问题。只要我们认真分析题意,选择恰当的方式,就能化另为整、化难为易,从而迅速地解决问题。
《浅谈整体思想───2005届初二盛维维》有一个想法