前一篇文章《西姆松定理及其退化形式》中提到了,圆上的点退化成圆外的点,结果发生了许多有趣的现象。如果将这样的做法在下面的问题中进行会怎样呢?
一、一个熟悉的问题
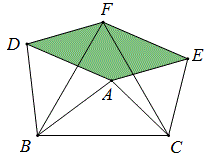
如图,△ABC中,∠A≠60°,在三角形同侧作三个正三角形ABD,ACE,BCF,那么四边形DAEF为平行四边形。
二、问题变式
当点A移动到△FBC的外接圆上时,平行四边形DAEF消失,四点共线了。
所以当△ABC与△FBC同侧时,∠A不能等于60°;当△ABC与△FBC异侧时,∠A不能等于120°.
三、问题拓展
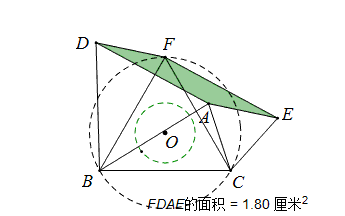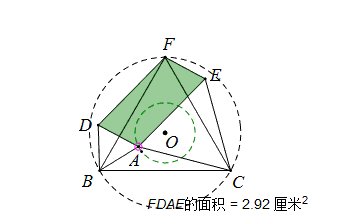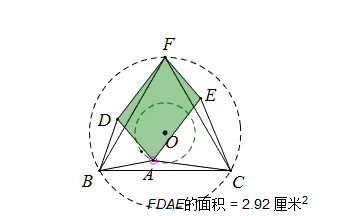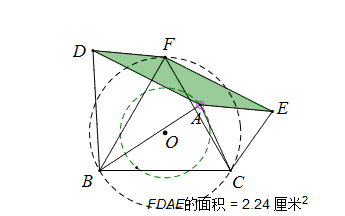
当A点在圆O的同心圆上移动时,情况如何呢?
与前一篇文章比较,何等相似,要的就是这个效果!平行四边形的面积在圆O上移动时面积不变,只有当圆O半径变化时面积才改变。
下面来证明当OA为定值时,平行四边形的面积也是定值。
如图,设△FBC外接圆半径为r,延长BA交EF于G,那么∠FGB=∠DAB=∠FCB,所以点G在圆上,
在△AEG中\dfrac{AE}{sin\angle{AGE}}=\dfrac{AG}{sin\angle{AEG}},即\dfrac{AE}{sin60^\circ}=\dfrac{AG}{sin\angle{DAE}},
即AEsin\angle{DAE}=AGsin60^\circ,
所以平行四边形AEFD的面积=
AD\cdot{AE}\cdot{sin\angle{DAE}}=AB\cdot{AG}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}|r^2-OA^2|,
故平行四边形的面积是常量。
四、问题再拓展
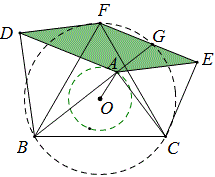
当我们以△ABC三边为边向同侧画相似三角形,结果又如何呢?
如图,三个黄色三角形相似(对应关系貌似不轮换),那么四边形ADFE为平行四边形,当F点在△ABC的外接圆的同心圆上转动时,平行四边形的面积为常量。
证明:
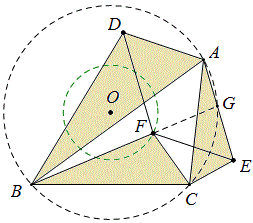
由△ABD∽△FBC可证△FBD∽△ABC,从而\dfrac{DF}{AC}=\dfrac{BF}{BC} ;
由△FBC∽EAC,从而\dfrac{AE}{AC}=\dfrac{BF}{BC} ,∴FD=AE,同理可证DA=FE,∴四边形ADFE是平行四边形.
延长BF交AE于G,由∠AGB=∠DFB=∠ACB,可得点G在⊙O上,
\dfrac{DF}{sin\angle{DBF}}=\dfrac{BF}{sin\angle{BDF}} ,即\dfrac{DF}{sin\angle{ABC}}=\dfrac{BF}{sin\angle{BAC}} ,
在△EFG中,\dfrac{EF}{sin\angle{FGE}}=\dfrac{EF}{sin\angle{ACB}}=\dfrac{FG}{sin\angle{GEF}} ,
平行四边形ADFE的面积
=DF\cdot{EF}\cdot{sin\angle{DFE}}=DF\cdot{EF}\cdot{sin\angle{GEF}}
=\dfrac{BF}{sin\angle{BAC}}\cdot{sin\angle{ABC}}\cdot{FG}\cdot{sin\angle{FGE}}
=|r^2-OF^2|\dfrac{sin\angle{ABC}sin\angle{ACB}}{sin\angle{BAC}},
故平行四边形的面积是常量。
推论:当E在⊙O上时,A、D、E、F四点共线
特别鸣谢:
本文和前一篇文章的部分关键的证明,由七中的樊贞惠老师提供,证明的思考过程之艰辛难于言表,特此感谢!