何为“计算法”?简言之,就是通过计算达到几何证明的目的。具体地说,某些几何问题虽然没有具体的数据,但可以设某些元素的量为单位1(或用字母表示),通过对一些角度、线段长度、面积等的计算来解决,这种方法称为计算法。
下面通过实例说明计算法是如何使用的。
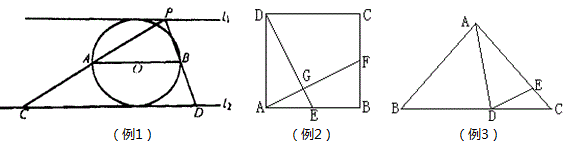
例1 如图,AB是⊙O的直径,l1,l2是⊙O的两条切线,且l1∥AB∥l2,若P是直线l1上一点,直线PA、PB交l2于点C、D,设⊙O的面积为S1,△PCD的面积为S2,则\frac{S_1}{S_2}= .
解:设AB=2,那么通过计算得S1=π,S2=4,∴\frac{S_1}{S_2}=\frac{\pi}{4}.
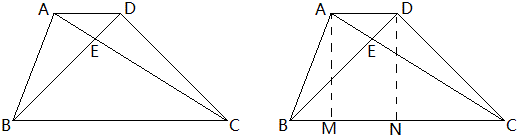
例2 如图E、F是正方形ABCD中AB、BC的中点,AB、BC交于G,求AG∶GF的值。
解:设AE=EB=BF=FC=1,那么DE=AF=\sqrt{5},
易证AF⊥DE,由面积法得AG=\frac{1\times2}{\sqrt{5}}=\frac{2}{5}\sqrt{5}.
例3 如图D在等腰三角形ABC的底边BC上,E在AC上,AE=AD,请你说明∠BAD=2∠EDC。
解:设∠B=∠C=m,∠ADE=∠AED=n,∠EDC=x,∠BAD=y。
由三角形外角性质得\begin{cases} n= x+m\\ n+x = y+m \end{cases},∴y=2x.
例4 如图,在梯形ABCD中,BD=DC,BD⊥DC,AC=BC,AC、BD交于E,求证:BE=BA。
分析:如果许多人画这个图形,可以想象,所画图形只有大小区分,形状是一致的。这就说明,所有角度是固定不变的,也就可以计算的,于是试试计算法,或许可以算出∠AEB和∠EAB的度数(一定相等)。梯形常用的辅助线是两条高。
证明:作梯形的高AM,DN,由已知,得
AM=DN=\frac{1}{2}BC=\frac{1}{2}AC,
故∠ACM=30°,∴∠EAB=75°,从而∠AEB=∠EAB=75°,故BE=BA。
通过以上4例可见,许多几何证明题,尤其是求比值的题,用计算法不失为妙法,屡试不爽。