问题21
本问题黑马提供,并解答如下:
问题22
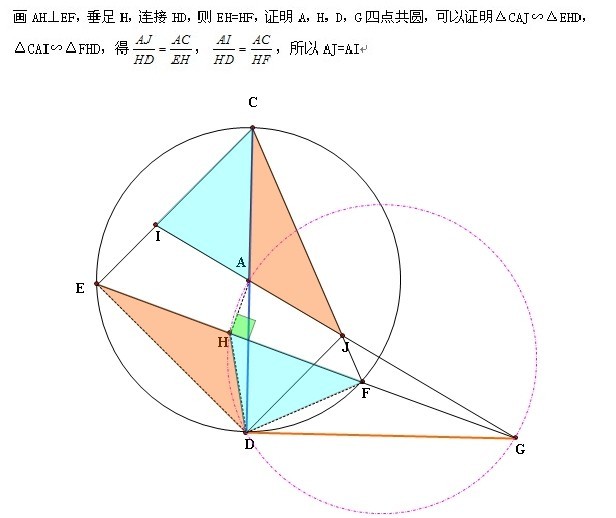
黄冈朱老师的解法
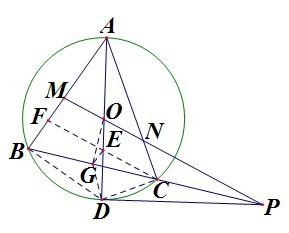
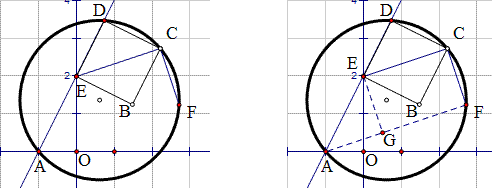
过O作OG⊥BC于G,过C作CF∥MN交AB于F,AD于E,连CE,通过证O、P、D、G和C、D、G、E两组四点共圆,得EG∥AB,得E是CF的中点即可.
问题23
黑马的解法
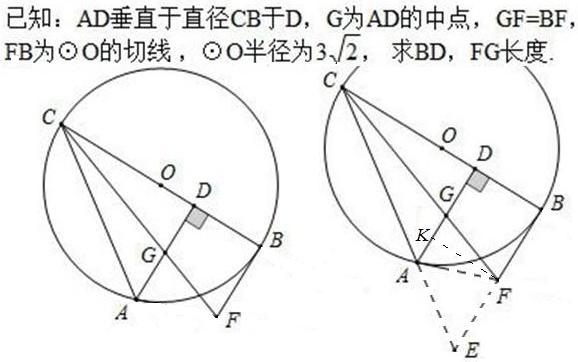
延长CA和BF交于E连AF,作FK⊥AD,由AD∥EB及AG=GD,得BF=EF,易证AF=BF=FG,故AK=KG,所以BF=KD=\frac{2}{3}DG,故\frac{CD}{CB}=\frac{DG}{FB}=\frac{2}{3},故BD=\frac{1}{3}CB=2\sqrt{2},FG=BF=DK=\frac{3}{4}AD=\frac{3}{4}\times16=12.
问题24
成都罗老师的解法:
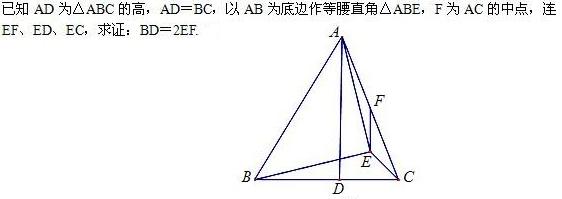
连结QF,作QI⊥BC,由已知A,B,D,E共圆,由中位线定理知QF=1/2BC=1/2AD=QI,又QB=QE,∠BQI=∠EQF,故△BQI≌△EQF,故BD=2EF。
问题25
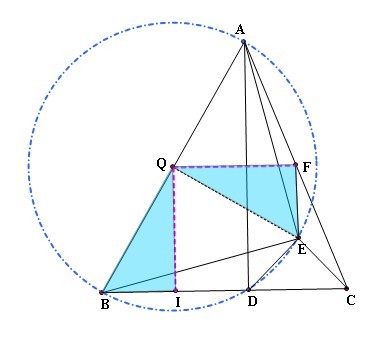
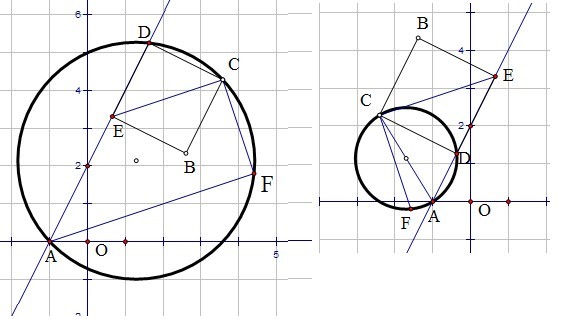
如图直线y=2x+2与x轴交于A,与y轴交于E,D在直线上,四边形DEBC是正方形,CF⊥CE交过A,D,C三点的圆于F,求证:CF定长。
成都罗老师的方法:
如图,连AF,作EG⊥AF于G,则由圆内接四边形对角互补,得∠F=90°,故ECFG为矩形,CF=EG=\frac{\sqrt{2}}{2}AE=\frac{\sqrt{10}}{2},所以CF为定长。
讨论:可以进行一些改编。
①E是直线上的一个定点,结论不变;
②当B在x轴上时,求圆的半径;
③E是直线上的一个定点,当CF=根号10时,求E点坐标。(本问题有2种情形,但答案一致)
可否改编出2种情形,2个不同答案的问题?可以继续讨论。
问题26
把一条线段分成3段,能构成三角形的概率是( )
A.\frac{1}{2} A.\frac{1}{3} A.\frac{1}{4} A.\frac{1}{6}
黑马的解答:
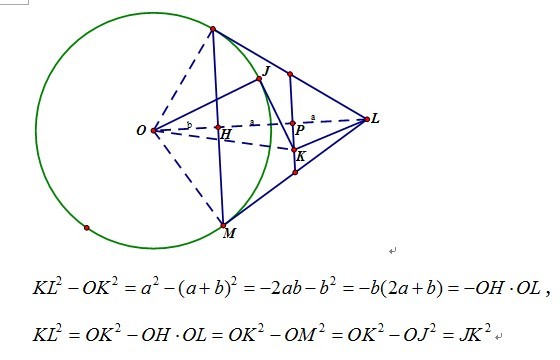
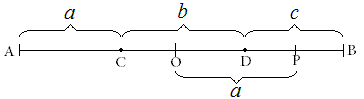
 我的思考:将一条线段AB分成3段,可以看作先在单位1的线段左边截取一条线段AC=a,再在剩下的线段左边截取线段CD=b,最后剩下的是DB=c,由于a<b+c,所以a<\frac{1}{2},故C点选择的概率是\frac{1}{2}。
我的思考:将一条线段AB分成3段,可以看作先在单位1的线段左边截取一条线段AC=a,再在剩下的线段左边截取线段CD=b,最后剩下的是DB=c,由于a<b+c,所以a<\frac{1}{2},故C点选择的概率是\frac{1}{2}。
同理,为使c<\frac{1}{2},D点必须取在AB中点O的右边,对称地考虑,D点也要在P的左边(BP=CO),我们不难计算OP=a,也即D点选取的长度在1-a中只有a的长度,所以D点选择的概率是\frac{a}{1-a}。
根据乘法原理总事件的概率是\frac{1}{2}\times\frac{a}{1-a}。
问题27
初三第二次月考试卷上有这样一道题:
已知正方形内接于半径为20、圆心角为90°的扇形(即正方形的各顶点都在扇形边或弧上),则正方形的边长是( )
A. 10\sqrt{2} B. 2\sqrt{10} C. 10\sqrt{2}或2\sqrt{10} D. 10\sqrt{2}或4\sqrt{10}
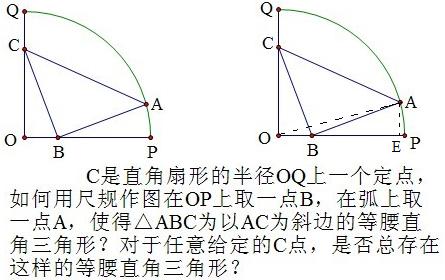
我看了这题,立即有个想法:直角扇形的内接正方形只有2个吗?有没有斜放的正方形呢?如果没有怎样证明?
我的问题得到蒋国刚老师的响应,他给出的命题是:
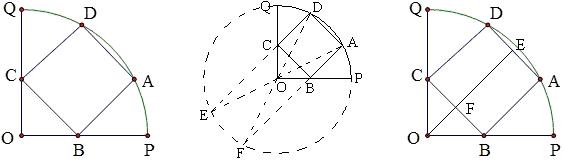
如图,正方形ABCD内接于直角扇形OPQ,其中A、D在弧上,B、C分别在半径上,求证:OB=OC.
蒋国刚老师的解答是:
如图,将扇形补全成圆,作直径DF,AE,则D,C,E和A,B,F均共线,于是△CDO≌△BAO,故OB=OC.
黑马觉得此命题的正方形可以弱化为矩形,圆心角可以弱化为0到180度的任意角,并给出了非常简单的证明方法:
如图作弦心距OE,交BC于F,由垂径定理易得CF=BF,故OB=OC.
原先我没有找到证明方法,想通过几何画板画图看看是否会有第三种正方形,于是设计了这样一个画图问题:
解决方法:如图连AO,作AE⊥OP于E,设半径为r,OC=a,OB=x,
有△OBC≌△EAB得BE=a,AE=x,由OA2=OE2+AE2,得r2=(x+a)2+x2,
解得x=\frac{-a+\sqrt{2r^2-a^2}}{2}
按照这个代数式的结构,可以用勾股定理作出x,从而作出点B和点A. 并且因为这个方程一定有唯一的正实数根,所以对于任意给定的C点,一定唯一存在这样的等腰直角三角形。
具体做法如下:
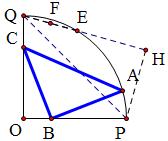 1、作Rt△PQH,使∠H=90°,PH=CO,QH交弧于E;
1、作Rt△PQH,使∠H=90°,PH=CO,QH交弧于E;
2、取QE中点F,在OP上截取OB=EF;
3、作BA⊥CB交弧于A。
结论:△ABC即为所求的等腰直角三角形。
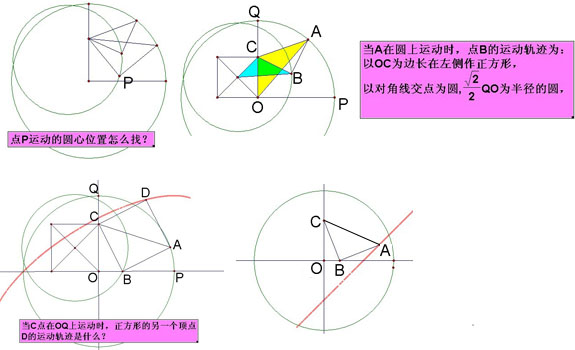
群友“伏龙山”还研究了一些点的运动轨迹。
问题28
初三第二次月考试卷上还有这样一道题:
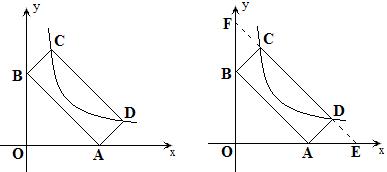
如图,矩形ABCD的顶点A,B分别在x,y轴上顶点C,D在反比例函数y=\frac{k}{x}的图象上,且AB=6,AD=2则k的值是 。
疑问:满足条件的矩形只有一种位置吗?
蒋国刚解答:只有一种位置,如图设直线CD交坐标轴于E,F,那么可以证明CF=DE,又CB=AD,所以△ADE≌△BCF,故∠OBA=∠OAB=45°.
问题29
黄冈朱老师提供问题并解答。
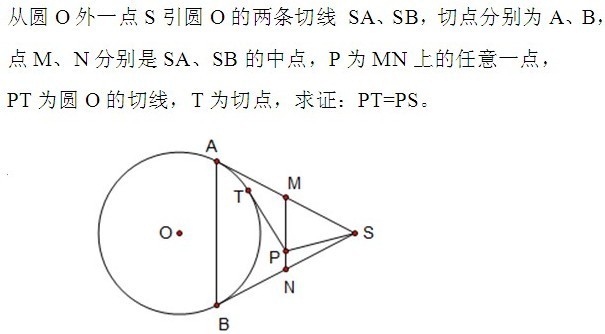
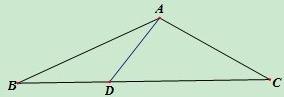
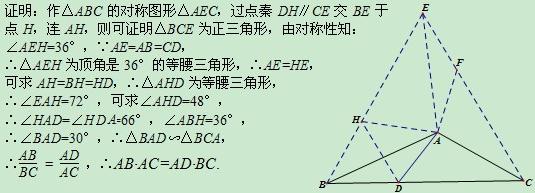
如图,△ABC中,∠B=24°,∠C=30°,D在BC上,DC=AB,求证:AB·AC=AD·BC.
解:

@匿名 你指的是27题吧,我在几何画板里试过了,达到最大值时是一个矩形,并不是正方形,这个应该可以用二次函数证明的。
黄老师,问题28,正方形ABCD内接于直角扇形OPQ,其中A、D在弧上,B、C分别在半径上,求证:OB=OC.把正方形改为矩形,当矩形的面积最大是我想就是正方形,该如何证明呢?