明明是假命题,却可以证明,显然证明有误,请你找出错误所在,赢得新初二,初三暑假练习各一套(共40份试卷)。你还等什么,赶快发表评论吧。
假命题1
任何三角形都是等腰三角形
证明:
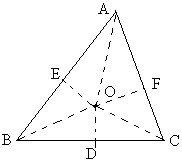
如图,作∠BAC的角平分线和BC的中垂线交于O,
过O作OE⊥AB,OF⊥AC,
我们不难证明,△AOE≌△AOF,△BOE≌△COF,
所以,AE=AF,BE=CF,所以AB=AC。
假命题2
有一组对角相等,一组对边相等的四边形是平行四边形。
已知:如图,在四边形ABCD中,AB=CD,∠B=∠D,求证:四边形ABCD是平行四边形。
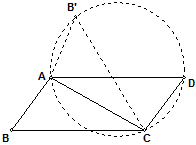
证明:
如图,将△ABC沿AC翻折得△AB′C,
∵∠B=∠D, ∴∠B′=∠D,
∴A、C、D、B′四点共圆,
∵AB=CD,∴AB′=CD,∴∠DAC=∠B′CA,即∠DAC=∠ACB,
∴△ABC≌△CDA,∴四边形ABCD是平行四边形。
谢谢两位老师的参与,他们都获得了我的奖品,本篇解题研究到此结束,欲得同样的奖品,请参与下一篇解题研究。
两个问题都是画图造成的
抱歉,问题2出在同圆中弦等,则弦所对的圆周角不一定等,同一条弦所对的圆周角可能互补
不知此修正是否可行?谢谢!
@aiav
谢谢aiav的参与。对你的第(2)条“翻折后A,B’,D可能一直线”我谈谈看法。因为翻折后A,B’,D一定在同一个圆上,故不可能在同一直线上,这说明你还没有找到原因。继续加油!
主要冲着两套试卷来的,无利不起早嘛。嘿嘿,不好意思!
1)点O在三角形的外部
2)翻折后A,B’,D可能一直线
初步想法,不知可行否?题目蛮有趣的