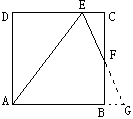一、前言
我国2001年颁发的《数学课程标准》指出:“能借助计算器进行复杂计算和探索数学规律……。在课堂教学、课外作业、实践活动以及考试中,应当允许学生使用计算器。”
由此可见,计算器进入初中数学课堂势在必行。以前,由于禁止学生使用计算器,结果加重了双基教学的任务,为了应付复杂的计算,学生从小学到初中都要进行大题量的操练。现在,计算器成了初中学生必不可少的学习工具,学生不仅仅摆脱了复杂的计算,而且改变了学习方式、思维方式,学习效益大为提高。
本文谈谈怎样正确引导学生合理使用计算器,使计算器成为促进双基教学的工具。
二、合理使用计算器促进双基教学
1、繁琐的计算被计算器替代
过去,在讲授数的运算时,教师既要讲清有关数的性质、运算法则,又要培养学生运算的熟练性,于是大量操练、烦琐的计算使学生应接不暇。现在,烦琐的计算被计算器替代,更多的时间可以化在“数的性质和运算法则”这个基本知识上,于是可以降低对计算技能的要求。
由于有了计算器,学生不再惧怕繁琐的计算,教师也用不着担心学生会因此丧失某种能力,只要对基本的计算能达到熟练的程度,这样做不会影响今后的学习。现在凡是直接按计算器能获得结果的题不再在考试中出现。
2、计算器使解题更加灵活
因为有了计算器,学生的解题就多了一种方法,探索能力、分析问题能力就会因此提高,这正是初中双基教学的要求(基本能力)。
例1.任意给定四个互不相同的数字,组成最大数和最小数,并用最大数减去最小数。对所得结果的四个数字重复上述过程,你会发现什么呢?
分析:本题是使用计算器提高探索能力的较好范例。假定所给的四位数是4321,那么4321-1234=3078,8730-3078=5652,6552-2556=3996,9963-3699=6264,6642-2466=4176,7641-1467=6147。
再试试其它的四位数也有同样的结果,即最后在7,6,4,1这四个数字进行死循环,也就是人们常说的“数字黑洞”。
下面来3道用计算器解决几何题的例子。
例2.如图,已知正方形ABCD中,E、F分别在DC、BC上,DE=3EC,EF平分∠AEC,求证:CF=BF。
分析:此题的常规解法是,如图延长EF和AB交于G,如果设AD=4a,容易求得DE=3a,AE=AG=5a,CE=BG=a,所以△CEF≌△BGF,所以CF=BF。
有位学生,他使用计算器的意识特别强,解法如下:
∵tan∠AED=\dfrac{AD}{ED}=\dfrac{4}{3} ,∴∠AED=53.13010235°,
∠CEF=63.43494882°,设CE=a,
∴CB=4a,CF=CE·tan∠CEF=a·tan63.43494882°=2a, ∴BF=2a, ∴CF=BF。
综合列式:CF=a\times[tan(180-tan^{-1}\dfrac{4}{3})\div2] =2a。
其中式子tan(180-tan^{-1}\dfrac{4}{3})\div2的按键顺序是:
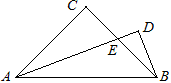
例3. 如图,等腰直角三角形ABC中,∠C=90°,AE是三角形的角平分线,BD⊥AE交AE延长线于D,求证:AE=2BD。
证明:∵∠CAE=22.5°,∴BD=ABsin22.5°
AB=\sqrt{2}AC,AC=AEcos22.5°,∴BD=AEcos22.5°×\sqrt{2}×sin22.5°=0.5AE
AEcos22.5°×\sqrt{2}×sin22.5°的按键顺序是:
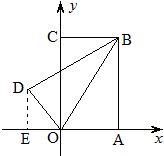
例4. 如图,在坐标系中有一矩形OABC,其中OB=\sqrt{5},tan\angle{COB}=\dfrac{1}{2},沿OB折叠矩形,使A落在第二象限的D点,求D点的坐标。
解:作DE⊥x轴于E,则∠BOA=tan-12,
∠DOE=180°-2tan-12,\dfrac{DE}{DO}=sin\angle{DOE},
DE= sin(180^{\circ}-2tan^{-1}2)=\dfrac{4}{5},所以OE=\dfrac{3}{5},所以点D的坐标是D(-\dfrac{3}{5},\dfrac{4}{5}).
3、计算器让数学问题更加生活化
数据可以更一般、更接近实际,可以利用计算器进行近似计算。
三、计算器使用不当会对双基教学造成威胁
计算器进入初中数学课堂以后,双基状况究竟如何呢?状况确实令人担忧!
1、学生在使用计算器过程中出现的现象
其一,是滥用计算器。
再简单的计算也依赖计算器,例如计算-2+3,\dfrac{1}{2}\times{4},\sqrt{9}等,本应心算完成的计算,很多学生都用计算器完成。这样做双基如何落实?
经调查,近60%的学生计算能力比较低或很低,这些人尽管手里掌握着计算器,但还是经常出错。究其原因,太依赖计算器了,对数已经没有了感觉,运算速度特别慢。
有一道作业,我批改后特有感受。
例5.(1)计算12-1= ;22-1= ;32-1= 。
(2)有一列数0,3,8,15,24,……,求第100个数是什么?
凡是平时滥用计算器的同学,就想不到两个小题的联系,就是说计算器泯灭了数感。
一天在因式分解复习课里,我要同学们做一道题:
例6.一个直角三角形的斜边为39,一条直角边为36,求另一条直角边。
完成后同学们报出了正确答案,经统计全班有92.3%的人是使用计算器完成的。接着我要求大家不用计算器完成计算,结果统计如下:
用方法1计算的占35.9%,用方法2计算的占23.1%,用方法3计算的占15.1%,还有25.9%的人不会算。
方法1 \sqrt{39^2-36^2}=\sqrt{1521-1296}=\sqrt{225}=15
方法2 \sqrt{39^2-36^2}=\sqrt{(39+36)(39-36)}=\sqrt{75\times3}=\sqrt{225}=15
方法3 \sqrt{39^2-36^2}=\sqrt{3^2(13^2-12^2)}=3\times5=15(13,12,5是一组勾股数)
由此看出,我们的学生摆脱计算器后,计算能力竟如此低下,虽然很多人使用计算器较快得出结果,但是却失去了巩固已学知识(如平方差公式、因式分解等)的机会。
其二,该用计算器的时候却想不到。
计算器不仅可以帮助我们完成计算题,还可以用来进行近似计算(估算)、检验结果是否正确、解决几何计算及证明、探索数学规律等,这是学生应具有的基本思想和技能,可是这一点学生差异很大,多数人缺乏这种思想和技能。
一次考试中有这样的题:
例7.按一定规律排列的一组数1,-\sqrt{2},\sqrt{3},-2,\sqrt{5},\cdots\cdots ,如果从1开始依次连续选取若干个数,使它们的和大于2,那么至少要 个数。
本题应该用用计算器依次相加,每加一次显示结果,直到和大于2为止。但是有很大一部分学生没有想到使用计算器这个工具。
2、教师在引导学生使用计算器的过程中出现的现象
其一,禁止学生使用计算器。
尤其是初一年级,很多数学教师下了这个禁令。也许这样的教师初衷是想提高学生的计算能力,但岂不知这是扼杀学生的创造力,剥夺学生的学习权利,加重学生的学习负担,是与新课标背道而驰的。
如果初一上禁止学生使用计算器是因为有理数的运算要过关的话,那么最迟在初一下要放开使用计算器。
其二,放任自流。
这样的教师对学生使用计算器的情况不闻不问,不加以正确引导,从而所教学生中滥用计算器的问题比较严重。
其三,命题时不考虑计算器的使用。
目前,学生所用的数学资料、试卷、日常作业中都会发现大量不合适的题目,这些题目在计算器开放的今天已经没有存在的必要了。但有些教师却忽略了这一点,结果往往达不到预期的效果。相反,旨在考察或培养学生使用计算器解决数学问题、探索数学规律的能力的题目少之又少。
以上现象导致了哪些后果?
计算器的使用在一定程度上是对初中数学双基教学的挑战,许多学生的双基是薄弱的,这是以上现象导致的最直接的后果。
学生经常在作业中暴露出以下的一些问题。
分数不约分(对两数之间的关系不敏感)
该近似不近似,不该近似取近似(计算器按惯了,没了感觉)
不知道问题与两数的大小有关(不知道在具体的情境中比较大小)
找不到一串数或一串等式的规律(对所给的数与序号之间的关系不敏感)
应用题中难以发现自己的答案明显不符合实际意义(对数的意义几乎没了感觉)
运算时往往找不到合理的算法(用了计算器最直接危害)
找不到问题中的数量关系(应用题中尤为突出)
……
你看!计算器正在挑战双基发展。
四、使用计算器后如何进行双基教学
计算器要不要进入数学课堂教学?答案显然是肯定的,问题是怎样合理使用。既不能放任自流,也不能简单禁止,而是要正确引导。首先教师自己要明确什么叫做合理使用计算器,其次应鼓励学生用计算器进行探索规律、估算和检验。
1、在双基教学时,应该禁止学生使用计算器
例如,有理数的运算、实数运算、解一元一次方程,合并同类项、乘法公式等入门教学,这是掌握运算法则、培养运算能力、锻炼数感的最佳时机。如果学生一味地用计算器进行运算,基础知识的教学就难以落实,双基教学的目标就难以达到。只要对学生讲清道理,分析利弊,认识危害,学生一定会积极配合,自觉地收起计算器,为打好扎实的运算基础,而进行法则练习。教师在布置作业时,数据尽量简单,方便学生心算。
一天,一个学生的有理数计算作业中,只有答案而没有过程,我找这位同学谈话。
师:你的作业为何只有答案没过程?
生:我用计算器算的,当然没有过程。
师:这样的计算怎么可以用计算器?
生:计算器不是开放了吗,为何不能用?
师:长期这样的话,计算法则就不能掌握。
生:有了计算器,没有法则也无妨。
师:那你就有所不知了!以后我们还要进行字母的运算,没有法则,计算器也无能为力了。
生:这……
经过这次谈话后,该学生以后的作业都写出了计算过程。
2、复杂的计算应让学生使用计算器
曾经有位朋友要我为他孩子作数学辅导,我发现他在计算多位数除法时用笔算,我非常诧异,问道:为何不用计算器?答曰:老师不让用,谁用了就缴谁的计算器。后来经了解,这所中学的数学老师都对学生提出了同样的要求。
初一有理数运算应该禁止使用计算器,但不应该用繁琐的数据为难学生。我认为,用求根公式解一元二次方程、用公式求抛物线的顶点坐标、近似计算、数据繁琐的实数运算等都应鼓励使用计算器。
一次实数运算课中,有这样一道题:
例8.计算(\sqrt{72}-\sqrt{27})\div\sqrt{5}(精确到0.01)
结果有许多同学先化简成最简形式,再用计算器计算。我就风趣地说:“怎么不直接用计算器计算,怕计算器累着?”学生笑了,他们知道了如何合理使用计算器。
3、加强心算能力
如果学生经常用计算器来计算简单的运算的话,无疑会使计算能力下降、速度减慢。
我在课堂教学时,经常利用各种机会对学生进行合理使用计算器的教育,要求学生多进行心算,经常传授一些简便运算的技巧。我班学生中有28%的人心算能力较强,77%的人简单的计算摆脱了计算器。
4、鼓励学生灵活使用计算器
许多学生只知道用计算器做计算题,其实探求规律、检验、估算等都可以用到计算器。我们再举一例。
例9.化简1+\sqrt{(1-\sqrt{2})^2}的结果是( )
A、\sqrt{2} B、3-\sqrt{2} C、2-\sqrt{2} D、2+\sqrt{2}
分析:只要用计算器求出原式的近似值(这个算式计算器只能显示近似值),再用计算器检验四个选项中哪个是正确的。
目前,学生所用的计算器,还有许多没有准确计算无理数的功能,上述方法适用范围就比较广泛。但是,仍有许多人想不到这样做,只能说没有让计算器物尽其用。
5、教师命题时要考虑到计算器的作用
计算器开放以后,原来常用的数学题,可能现在不合适了,达不到命题者的本意。但我们许多教师却不加理会,我行我素,依旧将这些题目放进试卷或练习中。可想而知,效度就大打折扣了。可悲的是,这样的题目在各种教辅材料里太多了。下面例举的数学题已经不适合作为考试题了,因为有了计算器,命题者的意图根本无法落实。
(1)比较下列各数的大小:3\sqrt{2} 2\sqrt{3};cos52° sin42°(学生不再用性质比较大小)
(2)当a= -1,b=2时,代数式5(a^2b-ab^2)-(ab^2+3a^2b)的值是 (可以不化简,而直接代入用计算器计算)
(3)已知\sqrt{13.2}=3.633,\sqrt{1.32}=1.149,那么\sqrt{132}= (有了计算器,条件多余)
(4)计算(-2)\times(-\dfrac{3}{8})^2-1\dfrac{7}{9}\div(-2\dfrac{2}{3})^2(计算器可以准确计算分数、平方根、特殊三角函数等)
(5)用科学计数法表示0.000381= (计算器有科学计数法表示的功能)
(6)已知ab=1,那么\dfrac{a}{a+1}+\dfrac{b}{b+1}= (可以取a=2,b=\dfrac{1}{2}代入用计算器计算)
等等。
6、教师要关注学生使用计算器的情况
在课堂教学时,是关注学生使用计算器的情况的最佳时候。不该用计算器的时候,数一数有几人用了;该用计算器的时候,数一数有几人没用。
批改作业时也应该关注学生使用计算器的情况,因为作业中可以看出哪些学生很依赖计算器,哪些学生能灵活使用计算器,还有哪些学生该用的时候没用。
学生是否合理使用计算器往往取决于教师的关注程度。当初一新生得知作业、考试都能用计算器,他们几乎到了欣喜若狂的地步,教师就应及早正确引导,坚持不懈地加以关注,相信一定会受到显著的成效。
五、调查问卷
我曾经向全校学生调查过计算器的使用情况,今有《学生使用计算器情况调查问卷》供你下载。
调查结果是:
全校问卷结果(单位:%)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | 45.4 | 21.5 | 30.9 | 14.7 | 41.3 | 36.0 | 71.6 | 38.1 | 2.1 | 40.7 | 对55.2 | 对66.0 |
| B | 45.3 | 33.9 | 49.5 | 53.7 | 40.4 | 28.4 | 25.1 | 37.9 | 33.2 | 35.1 | ||
| C | 6.4 | 42.9 | 14.9 | 16.1 | 15.5 | 12.4 | 2.4 | 21.3 | 59.5 | 11.7 | 错44.8 | 错34.0 |
| D | 2.9 | 1.7 | 4.7 | 21.0 | 2.8 | 35.1 | 0.9 | 2.7 | 5.2 | 12.5 |
从调查问卷的统计结果可以看出以下问题:
- 20%以上的学生不论怎样简单的计算题都用计算器,可想而知这些学生将丧失计算能力和数感。
- 近60%的学生计算能力比较低或很低,这些人尽管手里掌握着计算器,但还是经常出错。
- 只有15%的学生能经常想到用计算器探索规律。
- 随着年级升高,记不住计算器功能的学生逐渐增多。
- 从问卷第6题可以看出,学生不清楚什么是不合理使用计算器的做法,选择D的只有35.1%。
- 有近62%的学生认为不合理使用计算器的人在50%以上。
- 从11题可以看出,近一半人离开计算器就不会计算,在初二、初三中,只有6.8%的人会用最简便的方法。
- 从12题看,会用计算器进行无理数运算的人随着年级升高而增多,但是还是有34%的人不会用。