2017年11月13日下午进行一次说课,得到了郑瑄老师的指点,收获颇丰,现撰文如下。
一次函数第二课时教材里的内容就两个例题,见下图:
我的思路是:
1、说教材地位,即解读教材;
2、说教学目标、重点难点;
3、说两道题怎样教(将两题的解法有机结合起来,始终贯彻建模思想);
4、说为什么这样教;
5、说反思。
说课开始:
今天我说课的内容是,浙教版八年级上第五章5.3一次函数第二课时。
5.3一次函数第二课时是学生学习了坐标系、函数概念、一次函数概念后的教学内容,学生已经初步具有数形结合思想,方程思想,但还不具有函数思想。这节课是学生第一次接触利用函数解决数学问题和生活实际问题,这节课的意义在于让学生有意识使用待定系数法求函数关系式,树立建模思想。本课教学具有承上启下的作用,所谓承上就是本课的学习要用到已学的方程、方程组、应用题数量关系等。所谓启下就是本课的学习内容将作为学习其他函数、复数、向量、解析几何等的基础。
初中阶段学习函数的顺序,一般都是学习了函数的图象和性质后,再学习函数的应用。而本节课是倒置的,即先学习函数的应用(例4),再学习函数的图象和性质。我认为这样的做法有两个好处,其一是为了学习待定系数法更加有血有肉,其二是为了知识的学习螺旋上升,加强函数应用意识。
综上所述,我确定的教学目标是:
1、了解确定一次函数的条件;
2、掌握确定一次函数的方法;
3、建立函数思想,初步具有建立函数模型的思想与能力。
重点:例3是初中的核心知识—-待定系数法,它是确定各种函数关系式的主要方法,高中学习直线方程的多种形式皆以此为基础,所以是本课的重点。
难点:例4是利用函数解决的实际问题,学生从未经历过“提出问题→抽象→建模→解决问题”这种问题解决的途径,所以是本课的难点。
教学设计思路:
1、引入(例3)
(1)同学们,一次函数y=kx+b中哪些字母是变量?哪些是常量?
(2)哪些字母可以取不同的值?哪些字母在确定的函数中的值是固定不变的?
(3)如果给出条件“当x=3时,y=1”,k和b满足怎样的关系?常量能确定吗?要给出怎样的条件才能确定常量?
(4)如果给出条件是“当x=3时,y=1;当x=-2时y=-14”,如何确定函数关系式?
设计意图:上述问题(1)、(2)是与例4呼应,(3)是为了教学目标1设定,(4)是目标2的落实。这样设计的意图是让学生顺序渐进,学会用待定系数法求函数关系式,体会只有一个条件时是不能确定一次函数的,确定一次函数一般需要两个条件。
2、补充例子
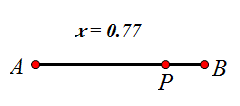
如图,在几何画板中点P在线段AB上,电脑能得到\dfrac{AP}{AB},点P移动这个比值也会随之变化。设这个比值为x,显然0≤x≤1,现在需要对x进行计算,计算得到的值是y,且5≤y≤12,请你设计一种计算的方法。
 解:设y=kx+b,由已知得:x=0,y=5以及x=1,y=12,用待定系数法求得y=7x+5,这个函数关系式就是计算方法。
解:设y=kx+b,由已知得:x=0,y=5以及x=1,y=12,用待定系数法求得y=7x+5,这个函数关系式就是计算方法。
设计意图:直接做例4难度太高,这个补充例子是一个过渡,既有待定系数法,又有函数的构建(构建的函数不唯一),难度适中,是沟通例3和例4的桥梁。
3、例4
书本中问题(1):“用什么方法描述”是无效的问题,因为这之前学生不知道“描述”的数学本意。故直接呈现问题(2),老师什么都不讲,直接让学生做。因为用小学方法做这题也不是太困难。
相信一定有不少学生因为小学解法掌握得不熟练,而无法解答,故能形成思维冲突,为构建函数打开局面。
师:现在我们换一种方法来解此题。本题涉及到的量有哪些?
生:1959年底沙漠面积、沙漠化的速度、经过的年数、沙漠面积、1998年沙漠面积100.6万公顷、2001年沙漠面积101.2万公顷。
师:这么多的量中哪些是变量,哪些是常量?
生:经过的年数和沙漠面积是变量,1959年底沙漠面积、沙漠化的速度是两个常量。
师:100.6万公顷和101.2万公顷是两个什么量?
生:是经过年数已知情况下的两个函数值。
师:为了写出这个函数表达式,需要引进几个字母?
生:四个,即经过的年数x(年)、沙漠面积y(万公顷)、1959年底沙漠面积b(万公顷)、沙漠化的速度k(万公顷/年)。
师:x、y、b、k之间有怎样的关系?
生:y=kx+b.
师:本题给出了几对变量的值?哪几对?
生:当x=3时,y=100.6,当x=6时,y=101.2.
师:如何确定函数关系式?
生:待定系数法。
……
师:解决本题的步骤有哪些?
生:①审题、理解题意;②确定常量与变量,构建函数模型;③根据两对变量的值确定函数关系式;④由自变量的值求出函数的值。
4、补充练习
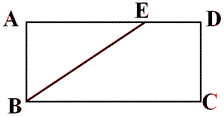
如图,矩形ABCD中,点E在AD上以每秒3个单位的速度从D运动到A.当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.求0.5秒时△ABE的面积.
解题步骤与例4完全相同。
例4师生的对话完全体现了启发式教学,在教师步步引导下,带领学生由小学的算术思想进入到函数思想,这是一个飞跃,实现这个飞跃难以使用探究性学习,更无法实行研究性学习。构建函数模型重点在于确定常量与变量,这在例3已经有铺垫。确定了常量与变量后,要选用几个字母,这些字母之间的关系如何?都不是问题,学生不难回答。
本节课的重点是待定系数法,但不是难点,学生比较容易掌握。难点是构建函数模型,这个是学生难以主动想到的,只有靠教师启发引导。所以在各个教学环节中,始终坚持环绕这个主题,让学生体会到上面的题目虽然可以用小学方法解决(包括补充练习),但构建函数模型是初中的方法,这不但是多了一种解题的方法,而是站在更高的高度审视问题中的数量关系。这对以后学生解决更难的问题创造了条件,奠定了基础。
本节课重点容易教学,难点的教学难在发现变量和常量,以及这些量之间的等量关系,学生很不习惯设四个字母,字母多了,他们心理有阴影,老师的任务就是帮助学生克服这个困难,消除阴影。在过去,学生往往习惯于寻找小学化的数量关系,即常量之间的关系,不习惯将变量参与到关系中,这就是缺乏函数思想的表现。如果说数量关系有三个层次,今天这节课就属于第三层次,三个层次分别是(1)已知数之间的关系(列算式就是这个关系);(2)已知数与未知数之间的关系(列方程就是这个关系);(3)常量与变量之间的关系(列函数式就是这个关系)。
列算式纯粹是已知数参与运算,列方程是已知数和未知数共同参与运算,而列函数关系式则有变量参与运算,参与运算的量范围扩大了,数量关系就更加丰富了、更加简单了,解决问题的路子就更广了。