一、教材地位
比例线段是学习相似三角形的基础,是利用相似三角形解决线段数量关系的前置内容.虽然小学已经学习过比例线段,但那时候比例只是用来解应用题,方法是根据数量关系列比例式,用“內项之积等于外项之积”的法则,将比例式化为等积式.
在初中不仅要继续小学的做法,还要进行比例式的各种变形,除了比例的基本性质,还有更比、反比、合比、分比、等比等等.参与比例的数从正有理数扩展到了实数和字母.利用比例进行更抽象的运算和数量分析,为解决几何中的数量关系奠定基础.
二、教学目标
- 了解比、比值、比例的概念.
- 能判别四个实数是否成比例.
- 能对一个比例式进行变形.
- 体会比例式左右两边变形的对应关系.
- 掌握“设k法”的运算技巧.
- 具有问题的反思意识,经历问题的探究过程.
三、重点和难点
重点:比例的基本性质和比例的变形运算是本节课的重点.
难点:例2涉及到的比例变形的技巧性强,学生不易想到,是本节课的难点.
四、教学过程
(一)知识回顾
比、比值、比例的概念,以问题形式回顾复习.
- 求9与6的比(答案是3:2,也可以是\dfrac{3}{2}).
- 求9与6的比值(答案是\dfrac{3}{2},也可以是1\dfrac{1}{2}或1.5).
- 9与6的比和\sqrt{18}与\sqrt{8}的比相等吗?这四个数成什么?写出相应的等式,这个等式叫做什么式?其中內项和外项分别是什么?
(二)“成比例”的定义
教材的定义中,a,b,c,d成比例,是否可以说b,a,c,d也成比例?这是许多老师有争议的问题.有人认为成比例的四个数是有循序的,我想回避这个争议.
(三)比例的基本性质
这个性质是双向的,可以先让学生将\dfrac{a}{b}=\dfrac{c}{d}化为积相等的形式,再将ad=bc化为比例式,然后得出\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow{ad=bc},并解释双箭头的含义.
有了这个性质,判定四个数是否成比例就有了第二种方法,当a>b>c>d,如果ad=bc,那么这四个数成比例,这样做的好处在于判别简单,一个比例式不成立,这四个数不一定不成比例,但用等积式判定时可以“一锤定音”.
例1 根据条件,求a:b的值.(1)2a=3b;(2)\dfrac{a}{5}=\dfrac{b}{4}.
第(1)题的结果是\dfrac{3}{2},写成3:2是不对的.
每道题做完后要检验,方法是化为等积.
第(2)题可以化等积式进行变形,化等积式是检验结果正确与否的依据,也可以用更比变形.
为了用更比解题,可以问学生下面的变形对不对:\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow{\dfrac{a}{c}=\dfrac{b}{d}},这就是更比.
练习1:P117作业题1及5,判断所给的四个数是否成比例.
1.下列各组数能否成比例?如果能成比例,请写出一个比例式.
(1)3,-9,-2,6.(2)\sqrt{12},\sqrt{6},\sqrt{10},\sqrt{5}.(3)3,\sqrt{3},\sqrt{2},2.
2.如图1,两块矩形绿地的一组邻边的长分别为a,b和c,d.已知这两块绿地的面积相等,a,b,c,d能否成比例?如果能成比例,请写出一个比例式.
方法2:用乘积判别是否成比例,若成比例,先求等积式,再化比例式.
(四)比例式的变形
比例式的变形技巧很多,比例的基本性质是最重要的,另外还有更比、反比、合比、分比和等比,例2是合比和等比.
例2 已知\dfrac{a}{b}=\dfrac{c}{d},判断下列比例式是否成立,并说明理由.
(1)\dfrac{a+b}{b}=\dfrac{c+d}{d};(2)\dfrac{a}{b}=\dfrac{a+c}{b+d}.
教学方法1:
老师启发思路、讲解方法、板演过程.
这样的方法即为讲授法.虽然高效、省时,但学生缺乏探究,学习被动.我想采用如下方法.
教学方法2:
每个同学先独立完成第(1)题,然后小组交流,对于学困生,在交流中获得解题思路,然后再分头独立做,学困生继续完成,已经解出一种方法的同学想第二种方法,然后由学生上台汇报成果.
解法1:\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}.
对于这种方法的同学,可以关注其思考过程,应该是从结论到条件的分析过程.
解法2:\dfrac{a+b}{b}=\dfrac{c+d}{d}\Rightarrow{ad+bd=bc+bd}\Rightarrow{ad=bc}\Rightarrow\dfrac{a}{b}=\dfrac{c}{d},再倒过来.
解法3:设\dfrac{a}{b}=\dfrac{c}{d}=k,则a=bk,c=dk,
∴\dfrac{a+b}{b}=\dfrac{b(k+1)}{b}=k+1,\dfrac{c+d}{d}=\dfrac{d(k+1)}{d}=k+1,
∴\dfrac{a+b}{b}=\dfrac{c+d}{d}.
本题是教学难点,为了突破难点,我采用的方法是先不讲直接让学生做题,做不出的人就会造成思维冲突,然后交流互助,多种方法解题,使学生易理解,易记忆,易掌握,多样的方法有利于解决第(2)题.
完成第(1)题后让学生填空:
已知\dfrac{a}{b}=\dfrac{c}{d},则\dfrac{a-b}{b}= ,\dfrac{a}{a+b}= ,\dfrac{b+a}{b-a}= .
然后请学生归纳这种变形的规律:比例式两边同法变形,如求\dfrac{a}{a+b}= ,即为![]() ,两边一样变形,所以\dfrac{a}{a+b}=\dfrac{c}{c+d}.
,两边一样变形,所以\dfrac{a}{a+b}=\dfrac{c}{c+d}.
这样归纳的目的为学习相似三角形打好基础、埋下伏笔.
做第(2)题时学生已经有上面的解题经验,可以请学生尽可能多的想出多种方法,这里的经验指的是①由结论到已知的分析法;②设k法.
解法1:\dfrac{a}{b}=\dfrac{a+c}{b+d}\Rightarrow{ab+ad=ab+bc}\Rightarrow{ad=bc}\Rightarrow\dfrac{a}{b}=\dfrac{c}{d},再倒过来.
解法2:设k法,即书上的方法.
解法3:\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\Rightarrow\dfrac{a+c}{a}=\dfrac{b+d}{b}\Rightarrow\dfrac{a}{b}=\dfrac{a+c}{b+d},这里运用了更比、合比的性质.
请学生归纳第(2)题变形的规律:一个比例式分子的和与分母的和之比的值不变.
(五)比例变形的应用
1.按已知的比例式求一个字母的值
练习2:P117作业题2
求下列各式中的x:
(1)3:x=6:12.(2)\dfrac{x-1}{x}=\dfrac{x-2}{x+1}.
方法:化等积,转化为一元一次方程.
2.按已知的比例式求两个字母的比值
练习3:P117作业题3
根据下列条件,求x与y的比:
(1)\dfrac{2x}{3}=\dfrac{3y}{2}.(2)\dfrac{x-2y}{y}=\dfrac{2}{5}.
方法1:化等积式;方法2:用比例的性质.
3.已知a与b的比值,求a、b组成的分式的值(分子、分母中的每一项都是同次的)
练习4:P117作业题4
已知\dfrac{a}{b}=\dfrac{3}{2},求下列算式的值:
(1)\dfrac{a-b}{b}.(2)\dfrac{2a-b}{a+2b}(a+2b\neq{0}).
方法:设k法.
4.几何图形中的比例
练习5:如图2,已知\dfrac{a}{b}=\dfrac{c}{d},a=2,b=4,求\dfrac{c}{c+d}的值.
练习6:如图3,两个三角形的边分别是a,b,c,和d,e,f,且a:b:c=d:e:f,a=9,b=6,求它们的周长之比.
补充这两个练习目的在于:
- 体现比例为几何服务的目的;
- 让学生熟悉连比;
- 进一步巩固合比、等比的知识.
(六)小结
小结的方法采用学生谈体会和收获,教师归纳的方法.我想用下面4句话归纳本课内容:
比化积来常秒杀,
左右两边同样化,
子和母和比不变,
设k不失好方法.

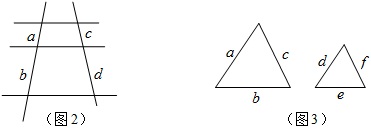
黄老师,我也出版了一本,我们交流一下吧,qq,756549412